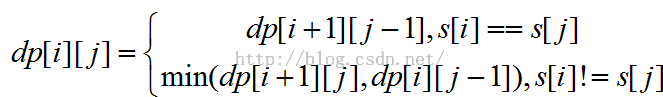- poj1159
Ruiyang_061X
dp。#include#include#includeusingnamespacestd;intN;stringa,b;intdp[2][5006];intmain(){cin>>N;cin>>a;b=a;reverse(b.begin(),b.end());for(inti=1;i<=N;i++)for(intj=1;j<=N;j++)if(a[i-1]==b[j-1])dp[i%2][j]=d
- POJ1159 Palindrome #最长公共子序列 滚动数组#
SDUWH_2U
XOJ
PalindromeTimeLimit:3000MSMemoryLimit:65536KTotalSubmissions:71974Accepted:24995DescriptionApalindromeisasymmetricalstring,thatis,astringreadidenticallyfromlefttorightaswellasfromrighttoleft.Youaretow
- POJ动态规划题目列表
咿呀而已
动态规划题目目录动态规划
POJ1050非常经典,用捆绑法将二维问题转化到一维的状态来求解。poj1050√最大子矩阵和:捆绑子矩阵转化为最大连续子段和问题poj1088√四方向记忆化搜索dp[i][j]=max(dp[i-1][j]...)+1遍历所有点,注意处理边界poj1163√数塔dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j]poj1159√dp[s][e]=min(dp
- 动规之区间动规小结
hhfgeg
▼动态规划★★★基础┠──>区间动规
区间动规主要有两种方法:一、是先想出递归式,然后将之转化为滚动数组。二、或者从小区间贪到大区间。POJ1159点击打开链接AC代码如下:#include#include#includeusingnamespacestd;chara[5005];shortdp[5005][5005];intmin(inta,intb){returna>n){memset(dp,0,sizeofdp);cin>>a+
- 刷题记录
tzyshiwolaogongya
数据结构
一、动态规划背包问题:poj3624(经典01)、poj1837(01)、poj1276(多重)、poj2063(完全)考虑前i位时的最优值dp[i]:poj3267(字典匹配)、poj1260(购买珍珠)LIS:poj2533(最长上升子序列)、poj1836(凸字型士兵身高)数字三角形:poj3176(数字三角形)LCS:poj1159(添加字母变成回文串)(区间dp也可)、poj1080(基
- poj1159 Palindrome (简单dp&&滚动数组)
婷霸
ACM解题记录dp
链接:http://poj.org/searchproblem?field=source&key=IOI+2000题意:至少增添多少个字符可以使原字符串变成回文串思路:原字符串反转,求最长公共子序列长度,剩余的长度就是需要加的字符数这里用到了滚动数组,因为该次的dp其实只取决去前一次的dp#include#include#includeusingnamespacestd;intdp[2][5010
- poj1159
Jazzmine
poj
【转】本文来自庞老板的CSDN博客,全文地址请点击:https://blog.csdn.net/code_pang/article/details/8759600?utm_source=copy动态规划法。设字符串为S,长度为L,d[i][j]表示以第i个字符为首,第j个字符为尾的字符串构成回文最少需要添加的字符个数,i和j的初值分别为1、L。如果S[i]==S[j],即字符串两端的字符相等,d[
- 【POJ1159】Palindrome(动态规划)
chenxiaoran666
POJ动态规划
题面:【POJ1159】Palindrome这道题是一道较水的DP题。我们可以用f[i][j]来表示把[i..j]这个区间变成一个回文串所需添加的最少字母数,这样我们就可以轻松地得到状态转移方程:当s[i]==s[j]时,f[i][j]=min{f[i+1][j-1],f[i+1][j]+1,f[i][j-1]+1};当s[i]!=s[j]时,f[i][j]=min{f[i+1][j]+1,f[i
- dp初步
bllsll
dp
CowBowlingPOJ-3176(数字三角形)poj2229B-Sumsets完全背包OR递推AppleCatchingPOJ-2385MilkingTimePOJ-3616n个任务,每个任务都有权值和时间区间,问你选哪些不重合的时间,使得权值最大Palindrome(回文数)poj1159问最少添加几个可以使之成为回文数LCSCheapestPalindromePOJ-3280LCS的变式H
- poj1159——Palindrome(组成回文串的最少字符数,dp)
BYSora
动态规划
DescriptionApalindromeisasymmetricalstring,thatis,astringreadidenticallyfromlefttorightaswellasfromrighttoleft.Youaretowriteaprogramwhich,givenastring,determinestheminimalnumberofcharacterstobeinserte
- poj1159——Palindrome(组成回文串的最少字符数,dp)
blue_skyrim
StringdppojAS
DescriptionApalindromeisasymmetricalstring,thatis,astringreadidenticallyfromlefttorightaswellasfromrighttoleft.Youaretowriteaprogramwhich,givenastring,determinestheminimalnumberofcharacterstobeinserte
- POJ 1159 Palindrome
TommyChok
POJ1159题目大意:给定一个长度为n的字符串,求至少添加多少个字符能使得它变成回文串解题思路:求原串的逆串(abcdd的逆串为ddcba),然后求原串与逆串的最长公共子序列,即为c,则n-c即为最少添加的字符(不懂如何证明,只能大脑大概过明白)求两个字符串a,b的最长公共子序列:定义状态dp[i][j]表示a的前i个字符和b的前j个字符的最长公共子序列,那么dp[len1][len2]即为所求
- [POJ 1159]Palindrome[DP]
CatGlory
dp
题目链接:[POJ1159]Palindrome[DP]题意分析:给字符串添加最少的字符让其成为回文串。解题思路:dp[i][j]代表,区间[i,j]变成回文要插入的最少字符数。如果s[i]==s[j],那么dp[i][j]=dp[i+1][j-1];否则,dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1(由已经构成回文的区间添加一个字符)。本题int,5000*5000
- poj1159
gu_solo
涉及算法:dp+lcs题目大意:对于给定的字符串S,求出最少需要在S中添加多少个字符可以使S对称(我们称此事S为回文串),即从左往右看s和从右往左看S是一样的,题目分析:两种思路思路一:设dp[i][j]为字符串S从第个字母到第j个字母S之间的这段字符串S(i,j)需要填加的字符数,使得S(i,j)为回文串。思路二:S中需要填加的字符数等于:S的长度-S和其逆序列S’的最长公共子序列的长度。用最长
- POJ1159 Palindrome 动态规划+滚动数组
Lxp丨小包子
ACM——POJ
POJ1159PalindromeDescription给你一个字符串,可在任意位置添加字符,最少再添加几个字符,可以使这个字符串成为回文字符串。SampleInput5Ab3bdSampleOutput2题解:解题关键:最少需要补充的字母数=原序列S的长度—S和S的倪序列的最长公共子串长度AC_Code(cpp):#include#includeusingnamespacestd;#define
- POJ1159 DPorLCS妙用
qq_21057881
POJ1159DPorLCS妙用一开始用的DP做,dp[i][j]表示从i到j这个区间成为回文需要增加多少个字符,如果s[i]==s[j],那么dp[i][j]=dp[i+1][j-1],否则dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1,状态转移方程应该不难理解,不过注意的是开了5000*5000的int数组会MLE,用了short类型飘过…做完搜了搜题解,居然是逆序
- poj1159 palindrome(动态规划+滚动数组)
动态规划
题目信息:Palindrome
利用动态规划+滚动数组,主要考虑到字符串比较长;
1 //Accepted 296K 688MS
2 #include<iostream>
3 #include<cstring>
4
5 using namespace std;
6 int c[2][5002];
7 char str1[5002],str
- poj1159 Palindrome 动态规划
动态规划
题目:回文是一个对称的字符串,换句话说,这个字符串从左到右读和从右到左读是一样的。给出一个字符串,你要编一个程序,决定要插入的最少的字符个数,使得原字符串成为一个回文。比如,字符串”Ab3bd”中插入2个字符,使得它能变成一个回文("dAb3bAd" 或 "Adb3bdA")。如果插入少于2个字符,将无法产生回文。求最少插入几个字符,使其变成回文字符串
分
- [POJ1159 Palindrome]
poj
[题目来源]:IOI 2000
[关键字]:动态规划
[题目大意]:把一个字符串变成回文串所需的最小步骤。
//=====================================================================================================
[分析]:因为回文串的要求是正着读和倒着读是一样的,即把这个字符串倒置后进行
- POJ1159(Palindrome)
poj
题目链接
题目大意,给定一个字符串,求至少需插入多少字符使其变成回文。动态规划题。
#include <stdio.h>#include <memory.h>#include <string.h> #define MIN(a,b) ((a)<(b)?(a):(b)) #define N 5001 char s[N]; int c[N]; int ma
- POJ1159 - Palindrome(区间DP)
poj
题目大意
给定一个字符串S,问最少插入多少个字符可以使字符串S变为回文串 题解
用dp[i][j]表示把字符串s[i…j]变为回文串需要插入的最小字符数
如果s[i]==s[j]那么dp[i][j]=dp[i+1][j-1]
如果s[i]!=s[j]那么dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1
可以用滚动数组优化一下空间 代码:
#include&l
- poj1159
poj
题意:求对字符串最少添加几个字符可变为回文串。
分析:简单做法是直接对它和它的逆序串求最长公共子序列长度len。n-len即为所求。(n为原串长度)
这样做的原因如下:
要求最少添加几个字符,我们可以先从原串中找到一个最长回文串,然后对于原串中不属于这个回文串的字符,在它关于回文串中心的对称位置添加一个相同字符即可。那么需要添加的字符数量即为n-最长回文串长度。
最长回文串可以看作是原串中
- poj1159——回文,lcs
poj
poj1159——回文,lcs Palindrome
Time Limit: 3000MS
Memory Limit: 65536K
Total Submissions: 54621
Accepted: 18892
Description A palindrome is a symmetrica
- 【One more】poj1159 Palindrome
more
又是一道水题…总觉得今天光做水题了…
.
题目是poj1159(http://poj.org/problem?id=1159),属于一道简单的动归。
题目如下。
【题目描述】给你一个字符串,你可以向里面的任意位置插入字符,问让这个串成为回文串最少要插入多少字符。
- POJ1159——LCS+滚动数组——Palindrome
poj
Description A palindrome is a symmetrical string, that is, a string read identically from left to right as well as from right to left. You are to write a program which, given a string, determines the
- POJ1159(动态规划+滚动数组)
动态规划
题意很明确,给你一个字符串,可在任意位置添加字符,最少再添加几个字符,可以使这个字符串成为回文字符串。
看到这道题,很熟悉,貌似以前做过,可就是想不起来解法,还是以前做的不认真。很惭愧,不过这次的解更优化。
解
- poj1159
poj
Palindrome
Time Limit: 3000MS
Memory Limit: 65536K
Total Submissions: 36646
Accepted: 12380
Description A palindrome is a symmetrical string, that is, a string re
- poj1159
poj
Palindrome
Time Limit: 3000MS
Memory Limit: 65536K
Total Submissions: 41570
Accepted: 14164
Description A palindrome is a symmetrical string, that is
- POJ1159
poj
Palindrome
Time Limit: 3000MS
Memory Limit: 65536K
Total Submissions: 43460
Accepted: 14815
Description A palindrome is a symmetrical string, that is
- POJ1159 Palindrome(dp加最少字母构成回文字符串)
hurmishine
字符串dppoj
PalindromeTimeLimit: 3000MS MemoryLimit: 65536KTotalSubmissions: 57426 Accepted: 19910DescriptionApalindromeisasymmetricalstring,thatis,astringreadidenticallyfromlefttorightaswellasfromrighttoleft.You
- Java实现的简单双向Map,支持重复Value
superlxw1234
java双向map
关键字:Java双向Map、DualHashBidiMap
有个需求,需要根据即时修改Map结构中的Value值,比如,将Map中所有value=V1的记录改成value=V2,key保持不变。
数据量比较大,遍历Map性能太差,这就需要根据Value先找到Key,然后去修改。
即:既要根据Key找Value,又要根据Value
- PL/SQL触发器基础及例子
百合不是茶
oracle数据库触发器PL/SQL编程
触发器的简介;
触发器的定义就是说某个条件成立的时候,触发器里面所定义的语句就会被自动的执行。因此触发器不需要人为的去调用,也不能调用。触发器和过程函数类似 过程函数必须要调用,
一个表中最多只能有12个触发器类型的,触发器和过程函数相似 触发器不需要调用直接执行,
触发时间:指明触发器何时执行,该值可取:
before:表示在数据库动作之前触发
- [时空与探索]穿越时空的一些问题
comsci
问题
我们还没有进行过任何数学形式上的证明,仅仅是一个猜想.....
这个猜想就是; 任何有质量的物体(哪怕只有一微克)都不可能穿越时空,该物体强行穿越时空的时候,物体的质量会与时空粒子产生反应,物体会变成暗物质,也就是说,任何物体穿越时空会变成暗物质..(暗物质就我的理
- easy ui datagrid上移下移一行
商人shang
js上移下移easyuidatagrid
/**
* 向上移动一行
*
* @param dg
* @param row
*/
function moveupRow(dg, row) {
var datagrid = $(dg);
var index = datagrid.datagrid("getRowIndex", row);
if (isFirstRow(dg, row)) {
- Java反射
oloz
反射
本人菜鸟,今天恰好有时间,写写博客,总结复习一下java反射方面的知识,欢迎大家探讨交流学习指教
首先看看java中的Class
package demo;
public class ClassTest {
/*先了解java中的Class*/
public static void main(String[] args) {
//任何一个类都
- springMVC 使用JSR-303 Validation验证
杨白白
springmvc
JSR-303是一个数据验证的规范,但是spring并没有对其进行实现,Hibernate Validator是实现了这一规范的,通过此这个实现来讲SpringMVC对JSR-303的支持。
JSR-303的校验是基于注解的,首先要把这些注解标记在需要验证的实体类的属性上或是其对应的get方法上。
登录需要验证类
public class Login {
@NotEmpty
- log4j
香水浓
log4j
log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, HTML, DATABASE
#log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, ROLLINGFILE, HTML
#console
log4j.appender.STDOUT=org.apache.log4j.ConsoleAppender
log4
- 使用ajax和history.pushState无刷新改变页面URL
agevs
jquery框架Ajaxhtml5chrome
表现
如果你使用chrome或者firefox等浏览器访问本博客、github.com、plus.google.com等网站时,细心的你会发现页面之间的点击是通过ajax异步请求的,同时页面的URL发生了了改变。并且能够很好的支持浏览器前进和后退。
是什么有这么强大的功能呢?
HTML5里引用了新的API,history.pushState和history.replaceState,就是通过
- centos中文乱码
AILIKES
centosOSssh
一、CentOS系统访问 g.cn ,发现中文乱码。
于是用以前的方式:yum -y install fonts-chinese
CentOS系统安装后,还是不能显示中文字体。我使用 gedit 编辑源码,其中文注释也为乱码。
后来,终于找到以下方法可以解决,需要两个中文支持的包:
fonts-chinese-3.02-12.
- 触发器
baalwolf
触发器
触发器(trigger):监视某种情况,并触发某种操作。
触发器创建语法四要素:1.监视地点(table) 2.监视事件(insert/update/delete) 3.触发时间(after/before) 4.触发事件(insert/update/delete)
语法:
create trigger triggerName
after/before
- JS正则表达式的i m g
bijian1013
JavaScript正则表达式
g:表示全局(global)模式,即模式将被应用于所有字符串,而非在发现第一个匹配项时立即停止。 i:表示不区分大小写(case-insensitive)模式,即在确定匹配项时忽略模式与字符串的大小写。 m:表示
- HTML5模式和Hashbang模式
bijian1013
JavaScriptAngularJSHashbang模式HTML5模式
我们可以用$locationProvider来配置$location服务(可以采用注入的方式,就像AngularJS中其他所有东西一样)。这里provider的两个参数很有意思,介绍如下。
html5Mode
一个布尔值,标识$location服务是否运行在HTML5模式下。
ha
- [Maven学习笔记六]Maven生命周期
bit1129
maven
从mvn test的输出开始说起
当我们在user-core中执行mvn test时,执行的输出如下:
/software/devsoftware/jdk1.7.0_55/bin/java -Dmaven.home=/software/devsoftware/apache-maven-3.2.1 -Dclassworlds.conf=/software/devs
- 【Hadoop七】基于Yarn的Hadoop Map Reduce容错
bit1129
hadoop
运行于Yarn的Map Reduce作业,可能发生失败的点包括
Task Failure
Application Master Failure
Node Manager Failure
Resource Manager Failure
1. Task Failure
任务执行过程中产生的异常和JVM的意外终止会汇报给Application Master。僵死的任务也会被A
- 记一次数据推送的异常解决端口解决
ronin47
记一次数据推送的异常解决
需求:从db获取数据然后推送到B
程序开发完成,上jboss,刚开始报了很多错,逐一解决,可最后显示连接不到数据库。机房的同事说可以ping 通。
自已画了个图,逐一排除,把linux 防火墙 和 setenforce 设置最低。
service iptables stop
- 巧用视错觉-UI更有趣
brotherlamp
UIui视频ui教程ui自学ui资料
我们每个人在生活中都曾感受过视错觉(optical illusion)的魅力。
视错觉现象是双眼跟我们开的一个玩笑,而我们往往还心甘情愿地接受我们看到的假象。其实不止如此,视觉错现象的背后还有一个重要的科学原理——格式塔原理。
格式塔原理解释了人们如何以视觉方式感觉物体,以及图像的结构,视角,大小等要素是如何影响我们的视觉的。
在下面这篇文章中,我们首先会简单介绍一下格式塔原理中的基本概念,
- 线段树-poj1177-N个矩形求边长(离散化+扫描线)
bylijinnan
数据结构算法线段树
package com.ljn.base;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Set;
import java.util.TreeSet;
/**
* POJ 1177 (线段树+离散化+扫描线),题目链接为http://poj.org/problem?id=1177
- HTTP协议详解
chicony
http协议
引言
- Scala设计模式
chenchao051
设计模式scala
Scala设计模式
我的话: 在国外网站上看到一篇文章,里面详细描述了很多设计模式,并且用Java及Scala两种语言描述,清晰的让我们看到各种常规的设计模式,在Scala中是如何在语言特性层面直接支持的。基于文章很nice,我利用今天的空闲时间将其翻译,希望大家能一起学习,讨论。翻译
- 安装mysql
daizj
mysql安装
安装mysql
(1)删除linux上已经安装的mysql相关库信息。rpm -e xxxxxxx --nodeps (强制删除)
执行命令rpm -qa |grep mysql 检查是否删除干净
(2)执行命令 rpm -i MySQL-server-5.5.31-2.el
- HTTP状态码大全
dcj3sjt126com
http状态码
完整的 HTTP 1.1规范说明书来自于RFC 2616,你可以在http://www.talentdigger.cn/home/link.php?url=d3d3LnJmYy1lZGl0b3Iub3JnLw%3D%3D在线查阅。HTTP 1.1的状态码被标记为新特性,因为许多浏览器只支持 HTTP 1.0。你应只把状态码发送给支持 HTTP 1.1的客户端,支持协议版本可以通过调用request
- asihttprequest上传图片
dcj3sjt126com
ASIHTTPRequest
NSURL *url =@"yourURL";
ASIFormDataRequest*currentRequest =[ASIFormDataRequest requestWithURL:url];
[currentRequest setPostFormat:ASIMultipartFormDataPostFormat];[currentRequest se
- C语言中,关键字static的作用
e200702084
C++cC#
在C语言中,关键字static有三个明显的作用:
1)在函数体,局部的static变量。生存期为程序的整个生命周期,(它存活多长时间);作用域却在函数体内(它在什么地方能被访问(空间))。
一个被声明为静态的变量在这一函数被调用过程中维持其值不变。因为它分配在静态存储区,函数调用结束后并不释放单元,但是在其它的作用域的无法访问。当再次调用这个函数时,这个局部的静态变量还存活,而且用在它的访
- win7/8使用curl
geeksun
win7
1. WIN7/8下要使用curl,需要下载curl-7.20.0-win64-ssl-sspi.zip和Win64OpenSSL_Light-1_0_2d.exe。 下载地址:
http://curl.haxx.se/download.html 请选择不带SSL的版本,否则还需要安装SSL的支持包 2. 可以给Windows增加c
- Creating a Shared Repository; Users Sharing The Repository
hongtoushizi
git
转载自:
http://www.gitguys.com/topics/creating-a-shared-repository-users-sharing-the-repository/ Commands discussed in this section:
git init –bare
git clone
git remote
git pull
git p
- Java实现字符串反转的8种或9种方法
Josh_Persistence
异或反转递归反转二分交换反转java字符串反转栈反转
注:对于第7种使用异或的方式来实现字符串的反转,如果不太看得明白的,可以参照另一篇博客:
http://josh-persistence.iteye.com/blog/2205768
/**
*
*/
package com.wsheng.aggregator.algorithm.string;
import java.util.Stack;
/**
- 代码实现任意容量倒水问题
home198979
PHP算法倒水
形象化设计模式实战 HELLO!架构 redis命令源码解析
倒水问题:有两个杯子,一个A升,一个B升,水有无限多,现要求利用这两杯子装C
- Druid datasource
zhb8015
druid
推荐大家使用数据库连接池 DruidDataSource. http://code.alibabatech.com/wiki/display/Druid/DruidDataSource DruidDataSource经过阿里巴巴数百个应用一年多生产环境运行验证,稳定可靠。 它最重要的特点是:监控、扩展和性能。 下载和Maven配置看这里: http
- 两种启动监听器ApplicationListener和ServletContextListener
spjich
javaspring框架
引言:有时候需要在项目初始化的时候进行一系列工作,比如初始化一个线程池,初始化配置文件,初始化缓存等等,这时候就需要用到启动监听器,下面分别介绍一下两种常用的项目启动监听器
ServletContextListener
特点: 依赖于sevlet容器,需要配置web.xml
使用方法:
public class StartListener implements
- JavaScript Rounding Methods of the Math object
何不笑
JavaScriptMath
The next group of methods has to do with rounding decimal values into integers. Three methods — Math.ceil(), Math.floor(), and Math.round() — handle rounding in differen