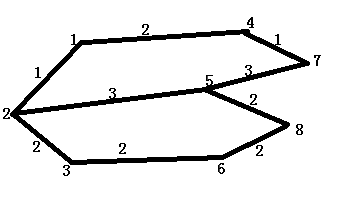
迪杰斯特拉初级练习

算法步骤：

（1）初始化：将源点Ｓ到图中各点的直接距离最为初始值记录Ｓ到各点的最短距离，不能直接到达记作ＩＮＦ，Ｓ到本身的距离为0。

（2）把所有其他除S的点放到集合Ｂ中，在所有集合B中遍历一个到S的最短路径距离的点u，并将其在集合B中取出。

（3）由新确定的u点更新S到集合B中一点v的距离为最短。

（4）重复以上2、3两个步骤。

基本思想：设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

时间复杂度：O(n*n)

空间复杂度（使用邻接矩阵存储时）：O(n*n)

练习：

NYOJ：115

城市平乱

时间限制： 1000 ms  |  内存限制： 65535 KB

难度： 4

描述

南将军统领着N个部队，这N个部队分别驻扎在N个不同的城市。

他在用这N个部队维护着M个城市的治安，这M个城市分别编号从1到M。

现在，小工军师告诉南将军，第K号城市发生了暴乱，南将军从各个部队都派遣了一个分队沿最近路去往暴乱城市平乱。

现在已知在任意两个城市之间的路行军所需的时间，你作为南将军麾下最厉害的程序员，请你编写一个程序来告诉南将军第一个分队到达叛乱城市所需的时间。

注意，两个城市之间可能不只一条路。

输入

第一行输入一个整数T，表示测试数据的组数。(T<20)
每组测试数据的第一行是四个整数N,M,P,Q(1<=N<=100,N<=M<=1000,M-1<=P<=100000)其中N表示部队数，M表示城市数，P表示城市之间的路的条数,Q表示发生暴乱的城市编号。
随后的一行是N个整数，表示部队所在城市的编号。
再之后的P行，每行有三个正整数，a,b,t(1<=a,b<=M,1<=t<=100)，表示a,b之间的路如果行军需要用时为t

数据保证暴乱的城市是可达的。

输出

对于每组测试数据，输出第一支部队到达叛乱城市时的时间。每组输出占一行

样例输入

1
3 8 9 8
1 2 3
1 2 1
2 3 2
1 4 2
2 5 3
3 6 2
4 7 1
5 7 3
5 8 2
6 8 2 

样例输出

4

来源

《世界大学生程序设计竞赛高级教程·第一册》改编

上传者

张云聪

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define Max 1000005
#define N 1050
using namespace std;
int dis[N];
int map[N][N];
int vis[N];
int armycity[N];
void dijkstra(int query,int v)//要查询的城市，节点数
{
    int i,j,k;

    for(i = 1; i <= v; i++)
    {
        dis[i] = map[query][i];//初始化,此处由于已经在之前处理过使得不能直接到达的点距离为INF
    }
    dis[query] = 0;

    for(i = 1; i <= v-1; i++)//遍历其它点到源点的最短路径
    {
        int min = Max;
        k = 0;
        for(j = 1; j <= v; j++)//在集合U中选取一个到源点距离最小的点k。
        {
            if(!vis[j] && min > dis[j])
            {
                min = dis[j];
                k = j;
            }
        }
        if(k == 0)//没有可以扩展的点
            return;
        vis[k] = 1;

        for(j = 1; j <= v; j++)//更新
        {
            if(dis[j] > dis[k] + map[k][j])
            {
                dis[j] = dis[k] + map[k][j];
            }
        }
    }
}
int main()
{
    int n,m,p,q;//部队数、城市数（节点数）、城市之间路的条数（边）、需要支援的节点。
    int a,b,c;
    int t;
    int i;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d%d",&n,&m,&p,&q);
        for(i = 0; i < n; i++)
        {
            scanf("%d",&armycity[i]);
        }

        memset(map,Max,sizeof(map));
        memset(vis,0,sizeof(vis));

        for(i = 0; i < p; i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            if(map[a][b] > c)
            {
                map[a][b] = c;
                map[b][a] = c;
            }
        }
        dijkstra(q,m);

        int ans = Max;
        for(i = 0; i < n; i++)
        {
            if(ans > dis[armycity[i]])
                ans = dis[armycity[i]];
        }
        printf("%d\n",ans);
    }
}

HDOJ 3790：

最短路径问题

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 9857 Accepted Submission(s): 3006

Problem Description

给你n个点，m条无向边，每条边都有长度d和花费p，给你起点s终点t，要求输出起点到终点的最短距离及其花费，如果最短距离有多条路线，则输出花费最少的。

Input

输入n,m，点的编号是1~n,然后是m行，每行4个数 a,b,d,p，表示a和b之间有一条边，且其长度为d，花费为p。最后一行是两个数 s,t;起点s，终点。n和m为0时输入结束。
(1<n<=1000, 0<m<100000, s != t)

Output

输出 一行有两个数， 最短距离及其花费。

Sample Input

       
       
       
       

        
        
        
        3 2
1 2 5 6
2 3 4 5
1 3
0 0
       
       
       
       

Sample Output

       
       
       
       

        
        
        
        9 11
       
       
       
       

#include<iostream>

#include<cstdio>
#include<cstring>
#define MAX 1000000
using namespace std;

int map[1005][1005];
int value[1005][1005];
int dis[1005];
int val[1005];
int vis[1005];

void dijkstra(int start,int n)
{
    int i,j,k,min;
    for(i = 1;i <= n; i++)
    {
        dis[i] = map[start][i];
        val[i] = value[start][i];
    }

    dis[start] = 0;
    val[start] = 0;

    for(i = 1; i <= n-1; i++)
    {
        min = MAX;
        k = 0;
        for(j = 1; j <= n; j++)
        {
            if(!vis[j] && min > dis[j])
            {
                min = dis[j];
                k = j;
            }
        }
        vis[k] = 1;
        if(k == 0)
            return;
        for(j = 1; j <= n; j++)
        {
            if(dis[j] > dis[k] + map[k][j])
            {
                dis[j] = dis[k] + map[k][j];
                val[j] = val[k] + value[k][j];
            }
            else if( dis[j] == dis[k]+map[k][j] && val[j] > val[k]+value[k][j] )
            {
                val[j] = val[k] + value[k][j];
            }
        }
    }
}

int main()
{
    int n,m;
    int i;
    int s,t;
    while(scanf("%d%d",&n,&m) && n+m)
    {
        int a,b,d,p;
        memset(vis,0,sizeof(vis));
        memset(map,MAX,sizeof(map));
        memset(value,MAX,sizeof(value));
        for(i = 0; i < m; i++)
        {
            scanf("%d%d%d%d",&a,&b,&d,&p);
            if(map[a][b] > d)//去重
            {
                map[a][b] = d;
                map[b][a] = d;
                value[a][b] = p;
                value[b][a] = p;
                //cout<<value[a][b]<<endl;
            }
        }
        scanf("%d%d",&s,&t);
        dijkstra(s,n);
        printf("%d %d\n",dis[t],val[t]);
    }
}