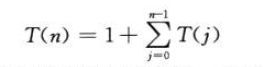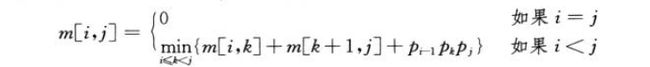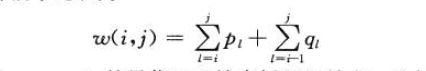第十五章 动态规划
动态规划一般用于寻找问题的最优解。与分治策略类似,都是将问题划分为相似的较小问题,对这些小问题求解再将这些小问题的解想组合得到最后的答案;与分治策略不同的地方在于将问题分为相似的小问题时,分治策略划分出的问题不会重叠,而动态规划的子问题产生了重叠。故我们将这些重叠的子问题的结果下来则可以避免重复计算子问题而提高效率。
15.1钢条切割
钢条切割问题再给定总长度和各个长度的收益的情况下求收益的最大值。
p为价格,r为收益我们通过如下公式来描述他
直觉上我们使用穷举法求解这个问题
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
def CUT_ROD(p, n):
if n == 0:
return 0
q = -float("inf")
for i in range(1, n+1):
q = max(q, p[i] + CUT_ROD(p, n - i))
return q
我们使用不变式验证其正确性并使用递归树分析其效率:
T(n)为指数函数,在可以选择切割或不切割的地方有n-1处,共有2^(n-1)种切割方案,当n增加1时,问题规模增加1倍。
观察递归树,存在诸多相同的子树,这意味着我们再执行算法的过程中反复的对一个问题进行求解。若将这些子树(子问题)的结果保存在备忘录中,在计算之前先检查备忘录中是否已经有该问题的解则可以避免重复计算的问题。由顶向下分解计算所有子问题,则只需要求解最深的一条边的问题,包含了所有子问题的解,其复杂度为O(lg(2^(n-1))) = O(n-1),遍历其n个子问题并将结果组合为最终结果则复杂度为O(n^2)
def MEMOIZED_CUT_ROD(p, n):
r = [-float("inf") for i in range(0, n+1)]
return MEMOIZED_CUT_ROD_AUX(p, n, r)
def MEMOIZED_CUT_ROD_AUX(p, n, r):
if r[n] >= 0:
return r[n]
if n == 0:
q = 0
else:
q = -float("inf")
for i in range(1, n+1):
q = max(q, p[i] + MEMOIZED_CUT_ROD_AUX(p, n-i, r))
r[n] = q
return q
我们也可以采用动态规划的方法来求解最优解:
1.刻画一个最优解的结构特征
2.递归的定义最优解得值
3.计算最优解得值,通常采用自底向上的方法
def BOTTOM_UP_CUT_ROD(p, n):
r = [0 for i in range(0, n+1)]
for j in range(1, n+1):
q = -float("inf")
for i in range(1, j+1):
q = max(q, p[i] + r[j-i])
r[j] = q
return r[n]
4.利用计算出的信息构造一个最优解
def EXTENDED_BOTTOM_UP_CUT_ROD(p, n):
r = [0 for i in range(0, n+1)]
s = [0 for i in range(0, n+1)]
for j in range(1, n+1):
q = -float("inf")
for i in range(1, j+1):
if q < p[i] + r[j-i]:
q = p[i] + r[j-i]
s[j] = i
r[j] = q
return r, s
def PRINT_CUT_ROD_SOLUTION(p, n):
r, s = EXTENDED_BOTTOM_UP_CUT_ROD(p,n)
print(r[n])
while n > 0:
print( s[n] )
n = n - s[n]
其复杂度为O(n^2)
15.2 矩阵链乘法
存在最优子结构和子问题重叠是应用动态规划的两个基本标示,我们应用动态规划的方法来求解最优括号化方案。
1.刻画一个最优解的结构特征
假设i<=k<=j为矩阵链乘法的Ai...Aj分割为两部分,使得m[i,j]为矩阵链乘法括号化的最优解,并且这个解可以由m[i,k]和m[k+1,j]和k点本身的信息表示出来,其中m[i,k]和m[k+1,j]都可以由独立求解。
2.递归的定义最优解得值
我们由公式表示m[i,j]
因为k点未知需要遍历一遍
3.采用自底向上的方法求解最优值
存在重叠子问题,采用自底向上的表格法求解问题
def MATRIX_CHAIN_ORDER(p):
n = len(p)
m = {}
s = {}
for i in range(0, n):
for j in range(0, n):
m[(i,j)] = 0
s[(i,j)] = 0
for l in range(1, n):
for i in range(0, n-l):
j = i + l
m[(i,j)] = float("inf")
for k in range(i, j):
q = m[(i,k)] + m[(k+1, j)] + p[i-1]*p[k]*p[j]
if q < m[(i,j)]:
m[(i,j)] = q
s[(i,j)] = k
return m, s
4.利用计算出的信息构造一个最优解
同样使用递归的调用分解出结果
def PRINT_OPTIMAL_PARENS(s, i, j):
if i == j:
print("A",i)
else:
print( "(")
PRINT_OPTIMAL_PARENS(s, i, s[(i,j)]),
PRINT_OPTIMAL_PARENS(s, s[(i,j)]+1, j),
print( ")" )
动态规划一般用于求解最优化问题,最优化问题应当具备两个要素:最优子结构和子问题重叠。
最优子结构是一种分治策略,发掘最优子结构,我们一般遵循如下模式,这也保证了该策略的正确性:
子问题图可以形象的回答这两个问题,另外我们需要确保子问题之间的无关性,既一个问题的解不会对另外一个问题的解产生影响。
重叠子问题的处理则避免了对相同子问题的仿佛求解,对与递归算法中每次求解效率得到提升。采用查表法记录子问题的解是典型的空间换时间的处理办法。若记录将子问题的解的表称为备忘录,所有递归算法维护同一个备忘录,若采用递归算法并在所有的递归层次中维护一个备忘录,则在递归中只求解了有必要求解的子问题,而自底向上的动态规划法会求解所有子问题。自底向上的动态规划的优势在于避免了递归调用的代价。
在求解最优解得过程中记录每个子问题的选择则可以在问题求解完成之后重构最优解。
1.刻画最优解结构
考虑其解得最优子结构若Z<z1, z2, z3...zk>为最长公共子序列,则有xi = yj = z(k-1),且zk为x[i,m]和y[j, n]的唯一公共元素。则很容易可以证明
则最优解结构可以通过“前缀”+zk构造出来
2.递归定义最优解的值
3.自底向上求解递归解
def LCS_LENGTH(X, Y):
m = len(X)
n = len(Y)
b = {}
c = {}
for i in range(0, m+1):
for j in range(0, n+1):
b[(i,j)] = ""
c[(i,j)] = 0
for i in range(1, m+1):
for j in range(1, n+1):
if X[i-1] == Y[j-1]:
c[(i,j)] = c[(i-1, j-1)] + 1
b[(i,j)] = "↖"
elif c[(i-1, j)] >= c[(i, j-1)]:
c[(i,j)] = c[(i-1,j)]
b[(i,j)] = "↑"
else:
c[(i,j)] = c[(i, j-1)]
b[(i,j)] = "←"
return c,b
4.重构最优解
def PRINT_LCS(b, X, i, j):
if i == 0 or j == 0:
return
if b[(i,j)] == "↖":
PRINT_LCS(b, X, i-1, j-1)
print(X[i-1])
elif b[(i, j)] == "↑":
PRINT_LCS(b, X, i-1, j)
else:
PRINT_LCS(b, X, i, j-1)
对于一个给定的概率集合,我们希望构造一棵期望搜索代价最小的二叉搜索树,我们称之为最优二叉搜索树。如有已排序的关键字集合K={k1, k2, ... , kn},ki的概率为pi,又有已排序的为关键字集合D={d0, d1, d2, ..., dn},有 di < ki < d(i+1), di的概率为qi。D作为叶子节点,构造一个搜索二叉树的期望代价最小。
与矩阵链乘法相似我们也可以通过动态规划来处理这个问题。
1.刻画最优解结构
若以r为根节点的从i到j的元素二叉搜索树为最优解表示为e = e[i,j],则集合中所有小于r的元素和所有大于r的元素,两者最优分别为e[i, r-1]和e[r+1, j]。r的取值为[i, j],若有k!=r使得期望搜索代价小于e[i, j],则有e[i, r-1]或者e[r+1, j]必不为最优解。
2.一个递归解
令w(i,j)为从[i,j]的元素的所有概率和,则最优解的递归解可以求得
3.计算最优二叉搜索树的期望搜索代价
书中p和q的下标采用不同计数,若采用q的计数只需要令q[0]=0即可。
def OPTIMAL_BST(p, q, n):
e = [ [0 for j in range(0, n)] for i in range(0, n+1)]
w = [ [0 for j in range(0, n)] for i in range(0, n+1)]
root = [ [0 for j in range(0, n)] for i in range(0, n+1)]
for i in range(1, n+1):
e[i][i-1] = q[i-1]
w[i][i-1] = q[i-1]
print(e)
for l in range(0, n):
for i in range(1, n-l):
j = i + l
print(i, j)
e[i][j] = float("inf")
w[i][j] = w[i][j-1] + p[j] + q[j]
for r in range(i, j+1):
t = e[i][r-1] + e[r+1][j] + w[i][j]
if t < e[i][j]:
e[i][j] = t
root[i][j] = r
return e, root
if __name__ == "__main__":
p = [0, 0.15, 0.1, 0.05, 0.1, 0.2]
q = [0.05, 0.1, 0.05, 0.05, 0.05, 0.1]
e, r = OPTIMAL_BST(p, q, 6)
print(e)
print(r)
习题解答