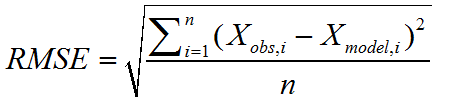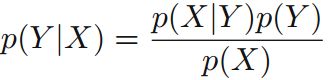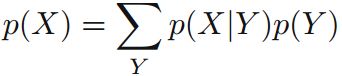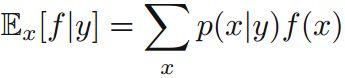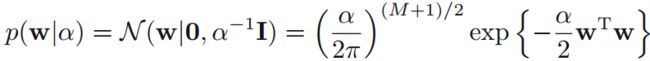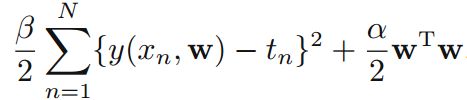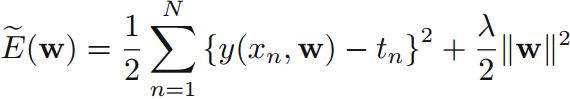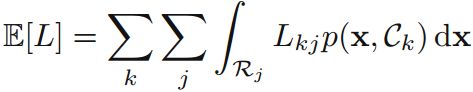模式识别与机器学习(一):概率论、决策论、信息论
本系列是经典书籍《Pattern Recognition and Machine Learning》的读书笔记,正在研读中,欢迎交流讨论。
基本概念
1.
模式识别(Pattern Recognition):是指通过算法自动发现数据的规律,并进行数据分类等任务。
2. 泛化(generalization):是指对与训练集数据不同的新样本进行正确分类的能力。(模式识别的主要目标)
3.
分类(classification):将输入数据分到有限个数的类别中。
4.
回归(regression):预测输入数据对应的输出值,该输出值由一个或多个连续变量的值组成。
5.
强化学习(reinforcement learning):在给定的环境或条件下,找到合理的步骤或操作使奖赏最大化。
其特点之一是:在发现新的操作(exploration)和利用现有操作(exploitation)之间进行权衡
。
6.线性模型(linear models):只包含线性的未知参数的模型,例如多项式就是线性模型。
7.
RMSE(Root-Mean-Square Error,均方根误差):观测值与真实值的偏差的平方和与观测次数之比的平方根。
(可以反映预测的准确性)
8. 在多项式曲线拟合中,多项式的阶数越高,参数的值也会越高。
当阶数过大时,将导致过拟合,此时参数的值非常大(正值)或非常小(负值),使拟合曲线出现很大的振荡。
解决过拟合的方法之一是:正则化,避免参数值过大或过小。
正则化参数(惩罚项)越大,参数值越小。
正则化参数过小,不能解决过拟合问题;正则化参数过大,将导致欠拟合。
9. 优化模型复杂度:使用验证集,交叉验证等等。
概率理论
模式识别中的不确定性(
uncertainty)一方面由于数据集的大小有限,另一方面是由于噪音。
概率规则:
加法规则(sum rule):
(marginal probability,边缘概率)
乘法规则(product rule):
1 贝叶斯理论(Bayes's theorem):
边缘概率可用加法规则计算:
先验概率(prior probability):某个类发生的概率(主观)。
后验概率(posterior probability):给定输入数据,其被分到某一类的概率。
2 期望与方差
条件期望(conditional expectation)=函数值 x 函数值发生的概率:
方差(variance):函数值和期望值的偏差的平方的期望值
对照:
协方差(covariance):
3 贝叶斯学派 vs. 频率学派
而贝叶斯学派认为:
参数w的值不是固定的,参数本身存在概率分布,而数据集(观测值)是固定的。
4 贝叶斯方法
在多项式曲线拟合中,我们
假设似然函数和先验分布服从高斯分布:
似然函数:
先验分布:
在训练集中通过最大化后验分布(MAP)求参数值:
等价于最小化以下公式:
该公式等价于正则化的误差函数平方和公式:
正则化参数等价于:
(MAP中已经包含了正则化项,也能解决over-fitting的问题)
5 预测分布(predictIve distribution)
在测试集中,预测分布为:
模型选择
交叉验证:
(1)S-fold cross-validation:将数据集分成S份,取其中的一份作为验证集,剩下的S-1份作为训练集;验证S次,每次取一份不同的验证集。
(2)leave-one-out:没份数据集刚好只有一个数据,适用于数据集稀少的情况。
不足:(1)训练次数随着S的取值增加,而某些情况下训练一次的计算开销就很大;
(2)不同参数的组合设置将可能导致训练次数的指数级增加。
The Curse of Dimensionality
(1)计算复杂度;
(2)不是所有低维空间的直观都能泛化到高维空间中去。
P(X=x1)是概率质量函数(probability
mass function),当且仅当,X是
离散变量。
P(X=x1)是概率密度函数(probability density function),当且仅当,X是连续变量。
决策理论
1. 最小化误分类率(the misclassification rate)
对于多类情况,则相当于:
2. 最小化期望损失(the expected loss)
不同的错误造成损失的不同,损失矩阵举例:
(矩阵说明:例如第一行“cancer”和第二列“normal”对应的值为1000,表示癌症患者被判定为正常的损失值为1000)
期望损失为:
3. 拒绝选择(the reject option):
当推理得到的最大后验概率不够大,难以判断时,则应该拒绝进行判断,另行处理(例如:由人工判断)。
4. 推理(inference)和决策(decision)
(2)
判别式模型(discriminative models):直接对后验概率 进行建模,一般比生成式模型的性能更好。
(可考虑组合使用生成式和判别式)
(3)
判别函数(discriminant function):构建直接将输入映射到输出的函数。
(例如,小于x0则属于类A,大于等于x0则属于类B)
判别函数的不足:
(1)若损失矩阵发生改变,则需要重新训练函数;
(2)因为判别函数不涉及概率,不能进行拒绝选择;
(3)若数据集中某一类的概率非常小,则训练得到的判别函数不准确;
(4)若有多个子任务,用判别函数则不能有效组合多个子任务的结果,从而不能有效进行有效的最终结果判断。
信息理论
1.
熵(Entropy)表示了信息的不确定性(随机变量传递的平均信息量):
若变量x和y相互独立,则信息量h(x):
出现该信息所对应的联合概率:
则信息量可被表示为:
那么熵则被表示为信息量的期望值:
可证明,当所有信息发生的概率都相等时,熵H最大,且最大值
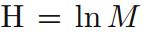 。
。
(每个信息出现的概率越不确定,熵的值越大,信息量也越大)
2.
条件熵(conditional entropy)
以离散变量为例证明条件熵公式:
3. 相对熵(relative entropy)和互信息(mutual information)
KL散度(KL divergence):
其中,q(x)是p(x)的近似分布。
可由Jensen不等式(凸函数的性质):
或
证明:
当且仅当q(x)=p(x)时,KL散度为零。即,KL散度可用于表示两个分布p(x)和q(x)的
不相似性。
若两个变量x,y不相互独立,为了测试其不相互独立的程度,引出
互信息:
当且仅当p(x, y) = p(x)p(y),即x和y相互独立时,互信息为零。
所以,互信息可用来表示两个变量的独立性,也可表示在给定变量y的情况下,变量x的不确定性的减少量。
(例如:先验分布和后验分布)