2015年北京师范大学新生程序设计竞赛题解

比赛链接

http://www.bnuoj.com/v3/contest_show.php?cid=7468

总结：

本次比赛一共8题，其中AB为签到题，CD为简单题，EF为中档题，G题为防AK题（但是由于spj的问题放了一份错误代码通过），H题为构造题（但是出题人的最初想法有误，并且由于只需输出解的存在性，出现了读错题却AC的情况），各题通过人数与难度大致符合，梯度尚可。

A. BQG's Programming Contest

直接输出min(60000,max(1000,5*max(t1,t2)))即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        printf("%d\n",min(60000,max(1000,5*max(a,b))));
    }
    return 0;
}

B. BQG's Messy Code

抄一遍代码可以发现这个程序会输出相反数，或者直接根据样例猜也可以。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int x;
        scanf("%d",&x);
        printf("%d\n",-x);
    }
    return 0;
}

C. BQG's Approaching Deadline

先做晚布置的作业不会使答案更优，因此将所有作业按照布置时间从小到大排序之后扫一遍即可，复杂度O(nlogn)，但是允许O(n^2)的排序通过。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=1005;
struct hw
{
    int a,b;
    bool operator < (const hw &t)const
    {
        return a<t.a;
    }
}s[MAXN];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=0;i<n;i++)
            scanf("%d%d",&s[i].a,&s[i].b);
        sort(s,s+n);
        int now=0;
        for(int i=0;i<n;i++)
        {
            now=max(now,s[i].a);
            now+=s[i].b;
        }
        printf("%d\n",now);
    }
    return 0;
}

D. BQG's Random String

直接模拟，复杂度O(n)。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const char t[4]="QAQ";
char s[100005];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%s",s);
        int n=strlen(s),res=0;
        for(int i=0;i+2<n;i++)
        {
            bool isok=1;
            for(int j=0;j<3;j++)
                if(t[j]!=s[i+j])isok=0;
            if(isok)res++;
        }
        printf("%d\n",res);
    }
    return 0;
}

E. BQG's Complexity Analysis

在大O意义下比较两个时间复杂度的大小是认为n->+inf的，因此优先比较n的幂次，n的幂次相同时再比较log的幂次，那么只需要先把特殊情况特判掉，再从字符串中将对应幂次提取出来即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
char s[55];
pair<int,int>c[5];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        for(int i=0;i<2;i++)
        {
            scanf("%s",s);
            int loc=0;
            if(s[2]=='1')
            {
                c[i]=make_pair(0,0);
                continue;
            }
            else if(s[2]=='n')
            {
                loc=3;
                if(s[3]=='^')
                {
                    int pp=0;
                    loc++;
                    while(s[loc]>='0' && s[loc]<='9')
                        pp=pp*10+s[loc++]-'0';
                    c[i].first=pp;
                }
                else c[i].first=1;
            }
            else c[i].first=0;
            if(s[loc]==')')c[i].second=0;
            else
            {
                int pp=0,len=strlen(s);
                while(loc<len && (s[loc]<'0' || s[loc]>'9'))loc++;
                while(loc<len && s[loc]>='0' && s[loc]<='9')
                    pp=pp*10+s[loc++]-'0';
                if(pp==0)c[i].second=1;
                else c[i].second=pp;
            }
        }
        if(c[0]<c[1])printf("First\n");
        else if(c[0]>c[1])printf("Second\n");
        else printf("Both\n");
    }
    return 0;
}

F. BQG's Confusing Sequence

需要分有0和没有0两种情况讨论，但是无论何种情形，混乱数都可以对应到二进制数，找到对应关系之后直接求出每一位的数字之后再取模即可，数位dp也是可以的，复杂度O(logn)。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll Mod=1000000007LL;
int ty[55];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int a,b,n;
        scanf("%d%d%d",&a,&b,&n);
        if(a>b)swap(a,b);
        if(a)n++;
        int loc=0;
        while(n)
        {
            ty[loc++]=n&1;
            n>>=1;
        }
        ll res=0LL;
        for(int i=loc-1-(a>0);i>=0;i--)
            res=(res*10+(ty[i] ? b : a))%Mod;
        printf("%lld\n",res);
    }
    return 0;
}

G. BQG's Square Glasses

由于折线上的点纵坐标>=1，因此除了最后一次切下来的正方形，其余正方形边长一定>=1，因此只会切出O(r)个正方形，直接按照题意模拟切正方形即可，那么问题在于每次如何找出最大的正方形，假设现在x<=p的玻璃都已经被舍去。

一个做法是，二分正方形的边长x(p+x<=r)，检查折线在[p,p+x]这一段的y坐标的最小值是否>=x，由于折线的性质，y坐标的最小值一定在边界或者拐点处，只需对拐点的y坐标预处理区间最小值，边界处的y坐标直接计算即可，需要二分快速定位边界所在线段并计算y坐标，这样的复杂度是O(nlogn+rlogrlogn)的。

另一个做法是，过点(p,0)引一条斜率为1的直线，设直线与折线的交点横坐标为q（如果有多个交点取横坐标最小的，如果没有交点取q=r），那么最大正方形的边长即为折线在[p,q]这一段的y坐标的最小值，容易知道p,q都是单调递增的，可以维护两个单调往右走的指针来记录折线上横坐标分别为p,q的点所在的线段，维护一个单调队列来记录区间[p,q]中折线拐点的y坐标的最小值，这样的复杂度是O(n+r)的。

下面给出第一种做法的代码。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double db;
const int MAXN=100005;
const db INF=1e100;
const db eps=1e-12;
int sgn(db x)
{
    if(x>eps)return 1;
    if(x<-eps)return -1;
    return 0;
}
db x[MAXN],y[MAXN];
db dp[MAXN][20];
int mm[MAXN];
void initRMQ(int n,db b[])
{
    mm[0]=-1;
    for(int i=0;i<n;i++)
    {
        mm[i+1]=((i&(i+1))==0) ? mm[i]+1 : mm[i];
        dp[i][0]=b[i];
    }
    for(int j=1;j<=mm[n];j++)
        for(int i=0;i+(1<<j)-1<n;i++)
            dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
db rmq(int x,int y)
{
    if(y<x)return INF;
    int k=mm[y-x+1];
    return min(dp[x][k],dp[y-(1<<k)+1][k]);
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=0;i<n;i++)
            scanf("%lf",&x[i]);
        for(int i=0;i<n;i++)
            scanf("%lf",&y[i]);
        initRMQ(n,y);
        db l=x[0]+eps,r=x[n-1]-eps,res=0.0;
        while(sgn(l-(r-1))<0)
        {
            int kl=lower_bound(x,x+n,l)-x-1;
            db yl=(y[kl+1]-y[kl])/(x[kl+1]-x[kl])*(l-x[kl])+y[kl];
            db tl=l,tr=r;
            for(int _=1;_<=100;_++)
            {
                db tm=(tl+tr)/2.0;
                int kr=upper_bound(x,x+n,tm)-x-1;
                db yr=(y[kr+1]-y[kr])/(x[kr+1]-x[kr])*(tm-x[kr])+y[kr];
                if(tm-l>min(min(yl,yr),rmq(kl+1,kr)))tr=tm;
                else tl=tm;
            }
            tl=(tl+tr)/2.0;
            res+=(tl-l)*(tl-l);
            l=tl;
        }
        printf("%.20f\n",res+(r-l)*(r-l));
    }
    return 0;
}

H. BQG's Quadrilateral Bricks

原题中“自相交四边形”这一情形已经被删去，现在题面已经修改，数据已经重做。

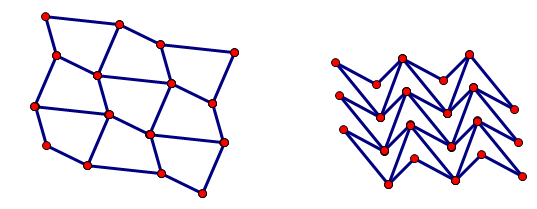
如上图，实际构造其实很简单，先将整个四边形关于某条边中点对称过去，得到一个中心对称图形，拉成一个无限长的条形之后可以发现两侧边界是相同的，利用这个长条就可以密铺整个平面，因此直接输出"BQG is happy!"即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        for(int i=0;i<8;i++)scanf("%*d");
        printf("BQG is happy!\n");
    }
    return 0;
}