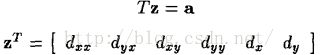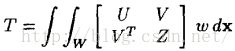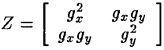Shi-Tomasi特征点（角点）检测及追踪方法

本文主要介绍了Shi-Tomasi特征点（角点）检测及追踪方法，这个方法是KLT方法的一种改进，其在检测特征点（角点）方法同KLT并没有什么不同，都通过比较梯度矩阵的最小特征值来确定特征点的，而主要的不同是在，匹配特征点时，其引入了仿射变换，让特征点在帧间匹配更为精确，并排除不好的特征点。另外还简要介绍了在估计图像运动向量的迭代方法—牛顿-拉夫逊方法或牛顿迭代法（Newton-Raphson method）。

 

一、牛顿-拉夫逊方法或牛顿迭代法（Newton-Raphson method）

本人前面在KLT角点检测方法里提到了可以通过迭代的方式，不断的应用新的位移向量d值，而图像块每次迭代都可以采用双线性插值（获得子像素精确度）得到新位置。那么这个迭代方法就是牛顿-拉夫逊方法Newton-Raphson。

下面是百度百科里的介绍：

 

二、Shi-Tomasi方法

图像匹配问题一般都通过图像之间相关性或者平方误差和等方法，如果是非常小的帧间移动，一个窗口可以通过优化一些匹配标准、或通过线性图像变形、或自适应窗口大小这些方法达到匹配最优。而特征窗口选择问题，可以通过一些基于纹理或角度（如高阶梯度，拉氏变换过零点，角点等）的方法来考虑，无论KLT还是Shi-Tomasi都是基于这样的考虑的。

Shi-Tomasi方法认为纯粹的平移对于图像运动来说，并不是适当的模型，而仿射变换（包含了线性变形及平移）却可以。然后提出了一种通过牛顿-拉夫逊方法Newton-Raphson来估计图像仿射变换的方法，但是其并没有用仿射运动来估计图像运动向量，而是使用了同KLT一致的平移运动来估计块的运动，因为实际上如果帧间运动比较小的情况下，平移比仿射运动估计效果更好。

随着图像帧的推进，图像强度改变模式会一种复杂的方式变化，我们可以简单地将图像运动视为如下公式：

这个运动为像素点的平移向量，可以写成仿射变换形式：

，

其中D是一个变形矩阵，而d是特征窗口中心的平移向量，而在第一帧的像素点x移动到第二帧的Ax+d位置，这里A=I+D，即

那么接下来，我们需要估计D与d里共6个参数，而这个估计的质量依赖于窗口的大小、窗口内的纹理程度、帧间的运动。如果窗口太小，那么D将会很难估计，因为小的窗口内估计运动数目太小，所有估计并不可靠，而窗口小却更适合跟踪，因为减少跟踪后图像的不连续性。所以来说，纯粹的平移在跟踪过程中更好。

文章内的实验表明：这两个运动模型的最好结合是纯粹平移作为跟踪，而仿射运动作为比较特征匹配质量。

虽然我们没办法让运动估计完美，但我们可以使估计后不相似程度最小，即使以下公式最小：

仍然有泰勒近似为：

不过同KLT方法里纯粹的平移不同的是，这里的g拥有6个参数

而平移变换为如下：

T与a的值我们也是可以求出来的，然后就能估计Z的值，这里我们仍然可以通过牛顿迭代法获得比较精确的值。

在跟踪过程中，我们可以只应用纯粹的平移运动估计（此时D为0），即可以得到运动估计d。这里的Z先前已经得到，而e可以是a的最后两个元素值。

总而言之，这个方法是通过a来确定前后两个帧图像之间的相似性，而通过e来估计图像间的运动

三、总结

Shi-Tomasi选择角点方法同KLT角点检测方法是相同，我也不再多说了，它同KLT方法最关键的不同在于，其对于两帧图像块相似性比较标准不同，其引入了仿射变换，让匹配更为精确，而其在追踪时，仍采用同KLT方法一样，都是通过简单平移来估计图像像素运动的。

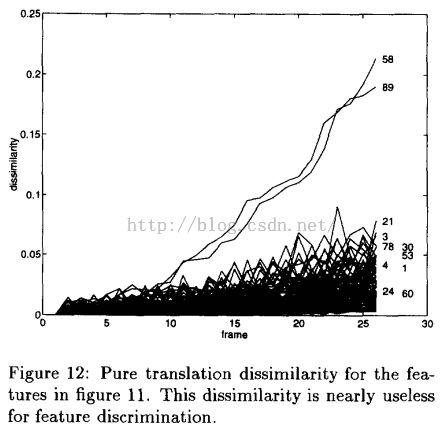
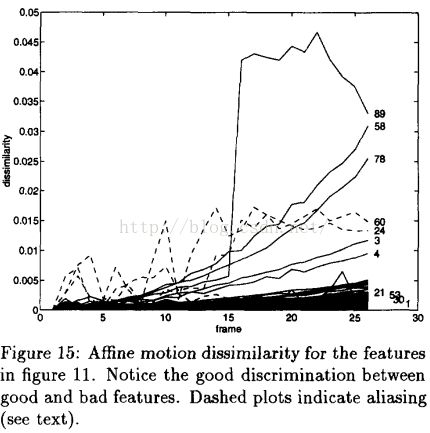
两者在追踪图像特征点的比较，可以发现左图不同特征点之间相似度变化线集中在一起，很难分辨出阈值出来，而右图应用了仿射变化的相似度衡量，可以清楚的检测出一些不好的特征点。

四、参考文献

Good Features to Track 【我的上传资源里有这篇文献】