CSU 1541 There is No Alternative【最小生成树+思维】

1541: There is No Alternative

Time Limit: 3 Sec   Memory Limit: 256 MB
Submit: 274   Solved: 74
[ Submit][ Status][ Web Board]

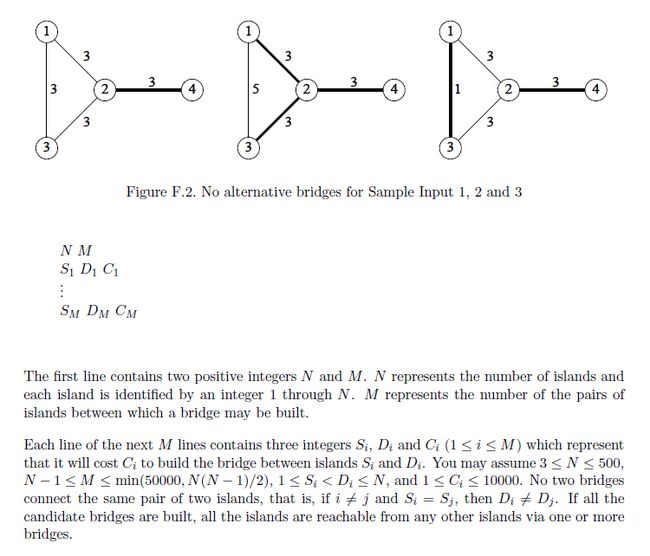
Description

 

Input

 

Output

 

Sample Input

4 4
1 2 3
1 3 3
2 3 3
2 4 3

Sample Output

1 3

HINT

Source

题目大意：给你n个点，m条边，求连接所有岛屿的权值和最小的边里边，哪些是必须建立的。

分析：其实就是在最小生成树中找到哪些边是必须建立的，并且求一下这些边的权值和。

思路：

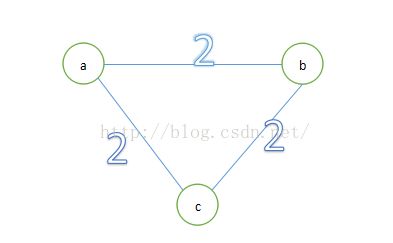
对于这样一种情况：

对于这个图的最小生成树的值很好看出权值和为4.对于这三条边，也很容易分析出没有哪一条边是在最小生成树里边必须建立的。但是如果是这样的情况：

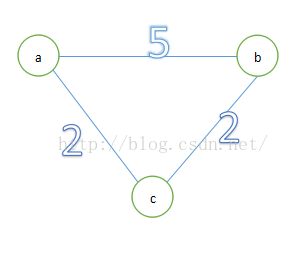
不难看出有两条边是必须建立的，分别是：a-c，b-c，那么我们到底要怎样判断一条边是否一定在最小生成树里边呢？

首先对于m条边排序，使用克鲁斯卡尔算法将每一条贪心入树的边都标记上，然后再对于这些个标记的边挨个枚举，如果去掉这个当前枚举到的边再求一下最小生成树的权值，如果权值等于第一次求的最小生成树的权值，辣么说明，这条边，在最小生成树里边，有，和没有，都是一样的，因为这个时候有其他边能够替代这条边形成一颗最小生成树（毕竟一个图里边最小生成树不一定是唯一的）。

辣么如果不等呢？那就说明这条边如果不建立的话，形成的图，无论能否形成一颗树（n-1条边），无论能否连通，如果权值不等于最小生成树的值，辣么说明这条边呢，没有了的话是形成不了正确的一颗最小生成树的。所以，这种情况，就是我们需要找的情况。

对于刚刚语言描述的代码实现：

        sort(a,a+m,cmp);//排序
        for(int i=0;i<m;i++)//求一下最小生成树的值
        {
            if(find(a[i].x)!=find(a[i].y))
            {
                merge(a[i].x,a[i].y);
                mst+=a[i].w;
                a[i].falg=1;//如果这条边能贪心入树，标记上，一会要枚举
            }
        }
        //printf("%d\n",mst);
        int cont=0;//必须建立的边的条数
        int sum=0;//权值和
        for(int i=0;i<m;i++)
        {
            //printf("%d\n",a[i].falg);
            if(a[i].falg==1)//枚举每一条在我们找到的最小生成树里边的边
            {
                init();//f【i】=i
                int tmp=0;
                for(int j=0;j<m;j++)
                {
                    if(i==j)continue;//去掉这条边
                    if(find(a[j].x)!=find(a[j].y))//求这个时候的最小生成树
                    {
                        merge(a[j].x,a[j].y);
                        tmp+=a[j].w;
                    }
                }
                //printf("%d\n",tmp);
                if(tmp!=mst){cont++;sum+=a[i].w;}//如果权值和最小生成树的权值不等，辣么说明这条边，是一定需要建立的。
            }
        }

最后是完整的AC代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
struct zuobiao
{
    int x,y,w,falg;
}a[1000000];
int mst;
int f[100000];
int find(int a)
{
    int r=a;
    while(f[r]!=r)
    r=f[r];
    int i=a;
    int j;
    while(i!=r)
    {
        j=f[i];
        f[i]=r;
        i=j;
    }
    return r;
}
void merge(int a,int b)
{
    int A,B;
    A=find(a);
    B=find(b);
    if(A!=B)
    f[B]=A;
}
int n,m;
int cmp(zuobiao a,zuobiao b)
{
    return a.w<b.w;
}
void init()
{
    for(int i=0;i<=n;i++)
    {
        f[i]=i;
    }
}
int main()
{
        scanf("%d%d",&n,&m);
        init();
        for(int i=0;i<m;i++)
        {
            scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].w);
            a[i].falg=0;
        }
        sort(a,a+m,cmp);
        for(int i=0;i<m;i++)
        {
            if(find(a[i].x)!=find(a[i].y))
            {
                merge(a[i].x,a[i].y);
                mst+=a[i].w;
                a[i].falg=1;
            }
        }
        //printf("%d\n",mst);
        int cont=0;
        int sum=0;
        for(int i=0;i<m;i++)
        {
            //printf("%d\n",a[i].falg);
            if(a[i].falg==1)
            {
                init();
                int tmp=0;
                for(int j=0;j<m;j++)
                {
                    if(i==j)continue;
                    if(find(a[j].x)!=find(a[j].y))
                    {
                        merge(a[j].x,a[j].y);
                        tmp+=a[j].w;
                    }
                }
                //printf("%d\n",tmp);
                if(tmp!=mst){cont++;sum+=a[i].w;}
            }
        }
        printf("%d %d\n",cont,sum);
        return 0;
}