bzoj-2286 消耗战【虚树+倍增lca+单调栈】
2286: [Sdoi2011消耗战
Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 1815 Solved: 645
[ Submit][ Status][ Discuss]
Description
Input
第一行一个整数n,代表岛屿数量。
接下来n-1行,每行三个整数u,v,w,代表u号岛屿和v号岛屿由一条代价为c的桥梁直接相连,保证1<=u,v<=n且1<=c<=100000。
第n+1行,一个整数m,代表敌方机器能使用的次数。
接下来m行,每行一个整数ki,代表第i次后,有ki个岛屿资源丰富,接下来k个整数h1,h2,…hk,表示资源丰富岛屿的编号。
Output
输出有m行,分别代表每次任务的最小代价。
Sample Input
1 5 13
1 9 6
2 1 19
2 4 8
2 3 91
5 6 8
7 5 4
7 8 31
10 7 9
3
2 10 6
4 5 7 8 3
3 9 4 6
Sample Output
32
22
HINT
对于100%的数据,2<=n<=250000,m>=1,sigma(ki)<=500000,1<=ki<=n-1
对于每次查询,如果用一次树型dp就能得出结果。
dp方程:
f[father]+=fmin(g[son]?inf:f[son],(min_e(son,father));(g[i]标记是否是关键点)
这个时间效率很直观O(m*n)
每次查询,我们只需要遍历关键点与关键点之间的lca,其它点时可忽略的或可跳跃的。
那么就需要用到虚树的技巧了,虚树就是通过维护一个单调栈把树的关键点和它们之间的lca按照dfs序遍历一遍,遍历的过程中通过单调栈的调整来理清树的父亲和儿子之间的关系。
首先,对树节点进行dfs。在期间对节点进行标号dfn。
然后,维护一个单调栈。这个单调栈的节点都在一条链上。
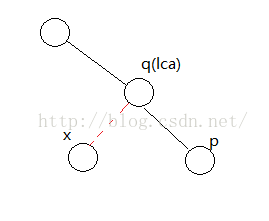
对于栈顶元素 p,栈次顶元素 q, 即将插入节点x 有如下关系:
1.lca是p.此时dfn(x)>dfn(p)=dfn(lca)
这说明 x在p的下面,直接把x入栈即可
2.p和x分立在lca的两棵子树下.此时 dfn(x)>dfn(p)>dfn(ilca)
这时候就有三种讨论了
针对这道题的连边就是树型dp处理
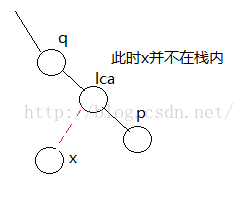
(1)如果dfn(q)>dfn(lca),可以直接连边q->p,然后退一次栈.
(2)如果dfn(q)=dfn(lca),说明q=lca,直接连边lca->p,把p退栈,此时子树已经构建完毕.
(3)如果dfn(q)<dfn(lca),说明lca被p与q夹在中间,此时连边lca->q,把p退栈,再把lca压入栈.此时子树构建完毕.
重复判断上述过程
这里处理 min_e(p,q) p到q的路径中权值最小的边。需要用倍增lca或者树剖也是可以的。这个参见《挑战程序设计竞赛》吧,改改代码就可以了
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <vector>
#include <algorithm>
#define find_min(a,b) a>b?b:a
#define MAX_V 250008
#define MAX_LOG_V 21
#define INF 0x3f3f3f3f
#define inf (1ll<<40)
using namespace std;
typedef long long int ll;
struct edge{
int to,cost;
};
vector<edge> G[MAX_V];
int par[MAX_LOG_V][MAX_V];//v节点向上走2^k步走到的节点
int mng[MAX_LOG_V][MAX_V];//v节点向上走2^k步中路过最小的边
int dfn[MAX_V];//每个点的dfs序标号
int dep[MAX_V];//深度
ll f[MAX_V];//树型dp
struct node{
int h,dfn;
}hs[MAX_V];
bool g[MAX_V];//是否是关键点
int sta[MAX_V*2];// 模拟栈
int icnt;//栈顶 、id
int swap(int &x,int &y)
{//交换
x=x^y;y=x^y,x=x^y;
}
//当前点、父亲节点 、深度、连接父亲点的边权
void dfs(int v,int p,int d,int pre_e)
{//lca搜索预处理
par[0][v]=p,dep[v]=d,mng[0][v]=pre_e,dfn[v]=icnt++;
for(int i=0;i<G[v].size();++i)
if(G[v][i].to!=p)
dfs(G[v][i].to,v,d+1,G[v][i].cost);
}
void init_tree()
{//预处理lca查询
icnt=0;//id初始化为0
dfs(1,-1,0,INF);
for(int k=0;k+1<MAX_LOG_V;++k)
for(int v=1;v<=MAX_V;++v)
{
if(par[k][v]<0)//超过树根
par[k+1][v]=-1,mng[k+1][v]=INF;
else
{//能前进 2^(k+1)步
int u=par[k][v];
par[k+1][v]=par[k][u];
mng[k+1][v]=find_min(mng[k][v],mng[k][u]);
}
}
}
int lca(int u,int v)
{
if(dep[u]>dep[v]) swap(u,v);
//先到同一深度
for(int k=0;k<MAX_LOG_V;++k)
if((dep[v]-dep[u])>>k & 1)
v=par[k][v];
if(u==v) return u;
//同时向上 二分查询
for(int k=MAX_LOG_V-1;k>=0;--k)
if(par[k][u]!=par[k][v])
u=par[k][u],v=par[k][v];
return par[0][u];
}
int min_e(int u,int v)
{
int ilca=lca(u,v);
int res=INF;
//u->lca
int mov;
if(dep[ilca]<dep[u])
{
mov=dep[u]-dep[ilca];
for(int k=0;k<MAX_LOG_V;++k)
if(mov>>k &1)
res=find_min(res,mng[k][u]),u=par[k][u];
}
//v->lca
if(dep[ilca]<dep[v])
{
mov=dep[v]-dep[ilca];
for(int k=0;k<MAX_LOG_V;++k)
if(mov>>k &1)
res=find_min(res,mng[k][v]),v=par[k][v];
}
return res;
}
void add_edge(int u,int v,int c)
{
G[u].push_back((edge){v,c});
G[v].push_back((edge){u,c});
}
void init()
{//初始化边数置0
for(int i=0;i<MAX_V;++i)
G[i].clear();
}
int cmp(const void *a,const void *b)
{
return ((node *)a)->dfn-((node *)b)->dfn;
}
ll fmin(ll a,ll b)
{
return a>b?b:a;
}
void solve(int k)
{
for(int i=1;i<=k;++i)
{
int o=hs[i].h;
hs[i].dfn=dfn[o];//同步搜索序id
}
qsort(hs+1,k,sizeof(hs[0]),cmp);
int tp=0;
sta[tp]=0;
sta[++tp]=1;
f[1]=0,g[1]=0;
for(int i=1;i<=k;++i)
{
int p=sta[tp],q=sta[tp-1],x=hs[i].h;
int ilca=lca(p,x);
while(dfn[p]>dfn[ilca])
{
if(dfn[q]<=dfn[ilca])
{
int tmp=fmin(g[tp]?inf:f[tp],(ll)min_e(p,ilca));
sta[tp--]=0;
if(ilca!=q)
sta[++tp]=ilca,f[tp]=0,g[tp]=0;
f[tp]+=tmp;
break;
}
else
{
f[tp-1]+=fmin(g[tp]?inf:f[tp],(ll)min_e(p,q));
sta[tp--]=0;
}
p=sta[tp],q=sta[tp-1];
}
if(sta[tp]!=x)
sta[++tp]=x,f[tp]=0;
g[tp]=1;
}
while(tp>1)
{
int p=sta[tp],q=sta[tp-1];
f[tp-1]+=fmin(g[tp]?inf:f[tp],(ll)min_e(p,q));
sta[tp--]=0;
}
printf("%lld\n",f[tp--]);
}
int main()
{
int n;
while(~scanf("%d",&n))
{
init();
int u,v,w;
for(int i=0;i<n-1;++i)
{
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w);
}
init_tree();
int m,k,h;
scanf("%d",&m);
while(m--)
{
scanf("%d",&k);
for(int i=1;i<=k;++i)
scanf("%d",&hs[i].h);
solve(k);
}
}
return 0;
}