ZOJ 3866 Cylinder Candy
题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5478
题面:
Cylinder Candy Time Limit: 2 Seconds Memory Limit: 65536 KB Special JudgeEdward the confectioner is making a new batch of chocolate covered candy. Each candy center is shaped as a cylinder with radius r mm and height h mm.
The candy center needs to be covered with a uniform coat of chocolate. The uniform coat of chocolate is d mm thick.
You are asked to calcualte the volume and the surface of the chocolate covered candy.
Input
There are multiple test cases. The first line of input contains an integer T(1≤ T≤ 1000) indicating the number of test cases. For each test case:
There are three integers r, h, d in one line. (1≤ r, h, d ≤ 100)
Output
For each case, print the volume and surface area of the candy in one line. The relative error should be less than 10-8.
Sample Input
2 1 1 1 1 3 5
Sample Output
32.907950527415 51.155135338077 1141.046818749128 532.235830206285
解:
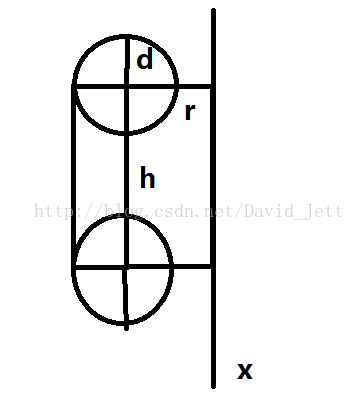
图形示意图。图形就是绕着x轴形成的旋转体。
推导过程:
体积:3部分。
1.除去上下的中间那个圆柱。 V1=pi*(d+r)*(d+r)*h;
2.上面两个小圆柱 V2=2*pi*r*r*d;
3.上下两个,类似圆环的东东。
先算出每一层圆环的面积,然后积分从0到d就是这个类环物的体积。
每一层圆环面积为S=pi*((sqrt(d*d-x*x)+r)^2)-pi*(r*r),=》 S=pi*(d*d-x*x+2*r*sqrt(d*d-x*x))即大圆减小圆。
然后积分从0到d,dx。V3=2*∫(0-d) (S)dx
比较难积的就是根号下d的平方减去x的平方。可以利用公式得∫(√a*a-x*x)dx=x/2*(√a*a-x*x)+a*a/2*arcsin(x/a)+C(C为常数,此处不需要,主要还是看旁边有没有积分表吧)
所以 Volume=V1+V2+V3。
表面积:
也分成3各部分计算。
1.上下两个圆 S1=2*pi*r*r
2.旁边圆柱侧面积 S2=2*pi*(r+d)*h
3.类圆环物的侧面积
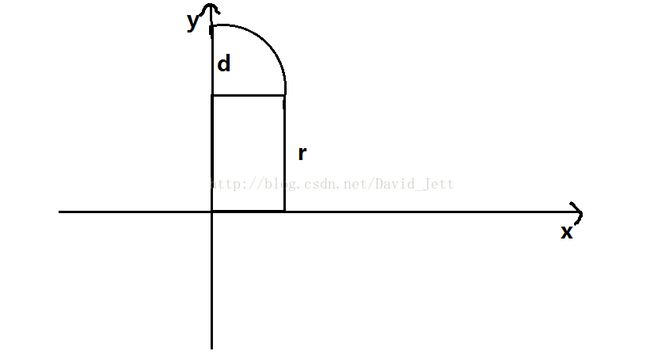
利用上述公式可以这样建图:
x=x ,y=sqrt(d*d-x*x)+r
利用旋转体侧面积代入S3=2*pi∫(0到d)f(x)*sqrt(1+f‘(x)^2)dx即可求得。 会用到∫dx/(sqrt(a*a-x*x))=arcsin(x/a)+C(C此处不需要)
S=S1+S2+2*S3
写得有点乱,见谅。
总结:比赛的时候,方法对了,表面积式子都代对了,就是2*pi这一项忘记分配到后面就错了,看来平稳的心态和整洁的草稿纸还是很重要的!!!
代码:
#include <iostream>
#include <cmath>
#include <iomanip>
#define pi 4*atan(1.0)
using namespace std;
int main()
{
int t,r,h,d;
cin>>t;
while(t--)
{
cin>>r>>h>>d;
cout<<fixed<<setprecision(12)<<2*(2*d*d*d/3.0*pi+r*d*d*pi*pi/2)+pi*((r+d)*(r+d))*(h)+pi*(r*r)*2*d<<" ";
cout<<fixed<<setprecision(12)<<2*(pi*pi*d*r+2*pi*d*d)+2*pi*r*r+2*pi*(r+d)*h<<endl;
}
return 0;
}