递归优化之尾递归

一个函数直接或间接调用自己本身,这种函数即为递归函数。

递归算法能够以一种优雅的思考方式简化问题，但由于递归通常是通过堆栈来实现的，一直背负着效率低的“臭名”。

以计算斐波那契数列为例，程序代码如下

	/**
	 *  采用递归方式计算斐波那契数列
	 */
	public  static long recursiveFib(long n)
	{
		if(n<0)		return -1;
		if(n <= 1)	return n;
		
		return recursiveFib(n-1)+recursiveFib(n-2);
	}

代码看起来很优雅简洁，但其运行效率奇低，运行测试代码

	public static void main(String[] args) {
		final int num = 50;
		long begin = System.currentTimeMillis();
		System.err.println("采用递归算法");
		long result = recursiveFib(num);
		long end = System.currentTimeMillis();
		System.err.println("fib("+num+")=="+result+"，耗时"+(end-begin)+"毫秒");
	}

运行结果如下

仔细思考一下该方法的计算过程，很容易知道问题所在，以计算fib(5)为例，其计算过程如下

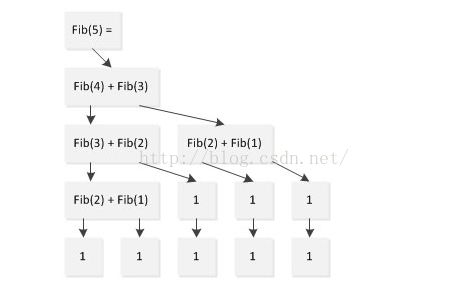
从上图可以看出，子问题的答案被重复计算。只要输入的参数稍微大点（例如100），程序就会因创建过多的堆栈而挂掉。

采用尾递归算法，可以极大地提高运行效率

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归。需要说明的是，只有当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时，这样的递归调用才是尾递归。

采用尾递归方式计算斐波那契数列，代码如下

/**
	 *  采用尾递归方式计算斐波那契数列
	 */
	public  static long tailRecursiveFib(long a,long b,int n)
	{
		if(n <0 ) return -1;
		if(n == 0) return a;
		if(n == 1) return b;
		
		//返回值出现在函数的末尾，且没有包含其他表达式，是尾递归！
		return tailRecursiveFib(b, a+b, n-1);  
	}

尾递归测试代码

	public static void main(String[] args) {
		final int num = 50;
		long begin = System.currentTimeMillis();
		System.err.println("采用尾递归算法");
		long result = tailRecursiveFib(0L,1L,num);
		long end = System.currentTimeMillis();
		System.err.println("fib("+num+")=="+result+"，耗时"+(end-begin)+"毫秒");
	}

代码运行结果如下

单从理论上比较两种算法，可以知道，尾递归至少有两点是比普通递归优秀的

1.尾递归通过迭代的方式，不存在子问题被多次计算的情况

2.尾递归的调用发生在方法的末尾，在计算过程中，完全可以把上一次留在堆栈的状态擦掉，保证程序以O(1)的空间复杂度运行。

遗憾的是，关于第二点，JVM并没有作出优化（运行上述尾递归函数，参数为10000，程序也会挂掉！！）

在函数式编程语言的世界里，充斥着大量的递归调用。在大部分函数式语言环境里，尾递归都是经过优化的。

下面采用Scheme-DrRacket（Lisp的一种方言）来展示尾递归的魅力，代码如下（语法有点奇怪，但不难理解）

(define (fib a b n)
  (cond
    [(< n 0) -1]
    [(= n 0) a]
    [(= n 1) b]
    [else (fib b (+ a b) (- n 1))])
)

示例运行结果如下（计算时间几乎可以忽略不计，请不要惊讶于计算结果如此之长）