Josephus(约瑟夫斯)问题
Josephus问题是下面的这个游戏:有N个人坐成一圈,编号为1至N。从编号为1的人开始传递热马铃薯。M次传递之后,持有热马铃薯的人退出游戏,圈缩小,然后游戏从退出人下面的人开始,继续进行。最终留下来的人获胜。比如:M=0,N=5, 5号获胜,退出顺序为1、2、3、4,5获胜;M=1,N=5, 3获胜,退出顺序为2、4、1、5。
思路一: 直接链表法。 将N个人排成环状队列,依次传递,通过程序说明(亲测无误):
/*********************************************************************************
头文件与命名空间
**********************************************************************************
#include <iostream>
#include <list>
using std::cin;
using std::cout;
using std::endl;
using std::list;
using std::list<int>;
int main()
{
/*********************************************************************************
准备工作
*********************************************************************************/
int person; // 人数
int transmit; // 传递基数(即题中的M)
cout << "GAME: JOSEPHUS" << endl << "Nums of persons: " ;
cin >> person;
cout << "transmit: ";
cin >> transmit;
/********************************************************************************
将N个人装入循环链表
********************************************************************************/
int num = 1; // 人员序号
list<int> list_person;
list<int> :: iterator iter1 = list_person.begin();
while (num <= person)
{
list_person.push_back(num++);
}
/*********************************************************************************
有N个人,会传递N-1次
********************************************************************************/
int N = person-1; // 传递次数
int m_transmit = 0; // 追随传递基数
while (N > 0) // 游戏开始
{
while (m_transmit<transmit && iter1!=list_person.end()) // 马铃薯还没有传递到末尾
{
m_transmit++;
iter1++;
}
if (m_transmit < transmit || iter1 == list_person.end()) // 当传递到末尾一人但是传递基数还没到M,要将马铃薯从头开始继续传
{
iter1 = list_person.begin();
continue;
}
cout << "erase: " << *iter1 << endl;
iter1 = list_person.erase(iter1); // 持有马铃薯的人退出游戏
m_transmit = 0;
N--;
}
if (iter1 == list_person.end()) // 有可能最后一次淘汰完人,链表指针指向this.end()处,所以要让指针回指到开始处
{
iter1 = list_person.begin();
}
cout << "The winner is: " << *iter1 << endl;
return 0;
}
运行结果图: M=1, N=5
思路二:逆推法
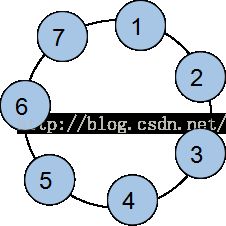
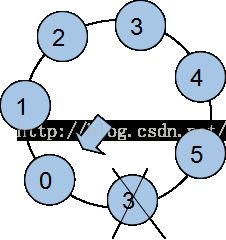
将游戏人数排成环状,如图a,为实验方便可将编号变为从0-N,如图b, 最后得出获胜编号为n,只要n+1就是实际编号
图a 图b
假设N=7,m=3。走过3步之后,3号出队,然后再从4号开始继续查找,实际上从这个时候开始,正是从N-1个元素里开始取元素了。我们可以
将第二轮的元素从4号开始重新以元素0为起始顺序进行查找。
一般的第一个人出队后,第一个出队的人编号必为m%N,剩下的N-1个人组成新的Josephus环,这时候以(m+1)%N开始。假定k=(m+1)%N,
他们组成新的序列,映射关系如下:
k-->0
k+1-->1
k+2-->2
......
k-3-->N-3
k-2-->N-2
k-1是前面一次遍历移除的。
说明对于N-1的环中,任何一个元素index对应到N的环中之间差了k,即(m+1)%N。这里的差不是直接相减差k,而是循环进位的结果。经分析可得出元素在N-1环和N环中对应的映射关系为index(N)=(index(N-1)+m+1)%N,接着移除元素,会发现映射关系index(N-1)=(index(N-2)+m+1)%(N-1);如此往复,会移除到只有一个元素的环,且index(1)=0,再逆着推,得index(2)=(index(1)+m+1)%2。通过归纳,得出数学规律: f(1)=0, f(N)=(f(N-1)+m)%N。 实际结果为f(N)+1。
代码(亲测无误):
#include <iostream>
using std::cin;
using std::cout;
using std::endl;
int person; // N
int transmit; // m
inline void init()
{
cout << "Josephus Game:" << endl << "The Number of Person: ";
cin >> person;
cout << "transmit: ";
cin >> transmit;
}
int main()
{
init();
int index = 0;
int person_trace = 1;
for (; person_trace != person; ++person_trace)
{
index = (index+transmit+1) % (person_trace+1);
}
cout << index+1;
return 0;
}
运行结果: N=7 m=1