神经元模型和网络结构
一:神经元模型
1.单输入神经元
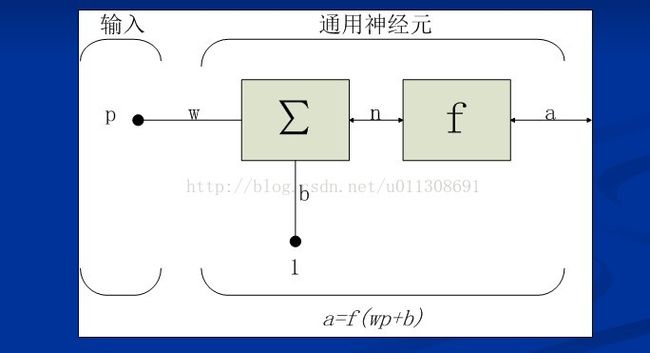
神经元是神经网络操作的基本信息处理单位。一个单输入神经元如下图所示。标量输入p乘上权值w得到wp,再将其送入累加器;另一个输入1乘上偏置值b,再将其送入累加器。偏置值b的作用是根据其为正或负,相应的增加或者降低传输函数的网络输入。累加器输出n通常被称为传输函数f的净输入,当n被送到传输函数f时,在f中产生神经元的标量输出a。
2.传输函数。
上图中的传输函数可以是n的线性或者非线性函数,可以用特定的传输函数满足神经元要解决的问题。下面将讨论三种传输函数:
(1)硬极限传输函数;
(2)线性传输函数;
(3)对数s形传输函数;
目前工程和设计中运用的传输函数有很多,常用的传输函数都在下表中。当然,也可以根据特定的问题定义自己需要的传输函数。
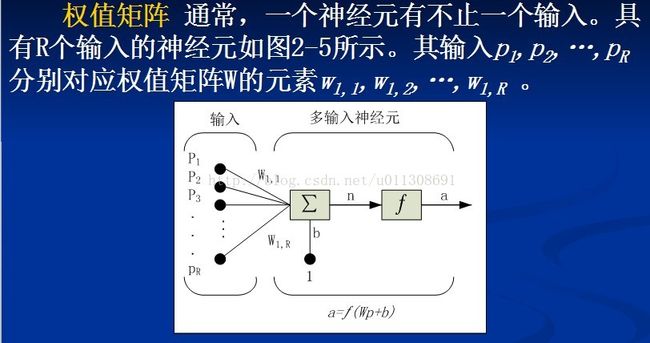
3.多输入神经元
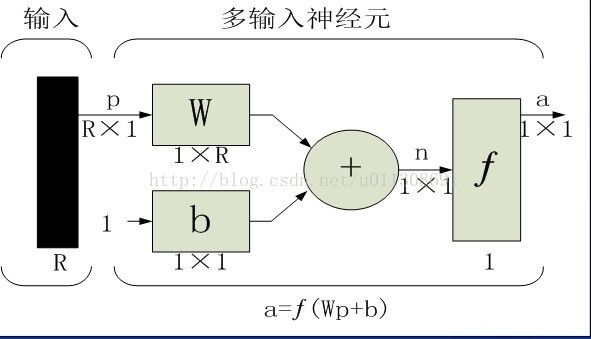
具有R个输入的神经元的简化符号
左边垂直的实心条表示输入向量p,p下面的变量R×1表示p的维数,也即输入是由R个元素组成的一维向量。这些输入被送人权值矩阵W,W有1行R列。
常量1则作为输入与标量偏置值b相乘。传输函数f的净输入是n,它是偏置值b与积Wp的和。在这种情况下,神经元的输出a是一个标量。如果网络有多个
神经元,那么网络输出就可能是一个向量。
请注意,网络的输入是由问题的外部描述决定的。
二:网络结构
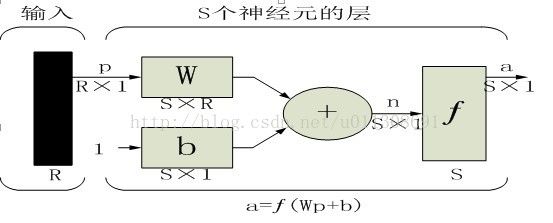
下图是由S个神经元组成的单层网络
该层包括权值矩阵、累加器、偏置值向量b、传输函数框和输出向量a。
输入向量p的每个元素均通过权值矩阵W和每个神经元相连。
输入向量通过如下权矩阵W进入网络:
同样,具有S个神经元、R个输入的单层网络也能用简化的符号表示为如图下所示的形式。
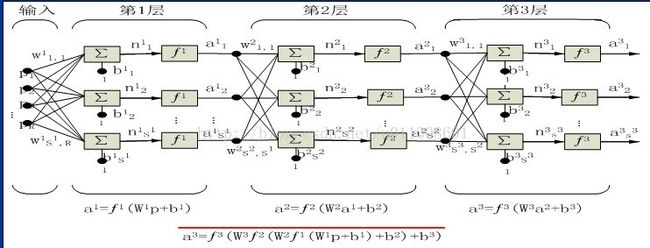
层上标 现在考虑具有几层神经元的网络。每个变量都附加一个上标来表示其所处层次。图下所示的三层网络就使用了这种标记方法。
输入层 隐含层 如果某层的输出是网络的输出,那么称该层为输出层,而其他层叫隐含层。
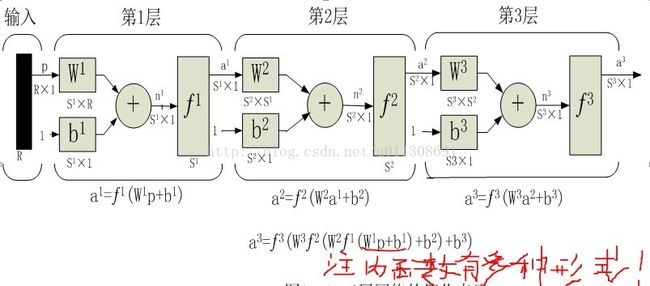
前面讨论的三层网络同样也可以用简化的符号表示,
递归网络
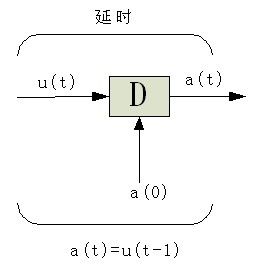
延时 在讨论递归网络前,首先介绍一些简单的构造模块。第一种是延时模块,如下图
积分器 另一种将用于连续时间递归网络的构造模块是积分器,如下图
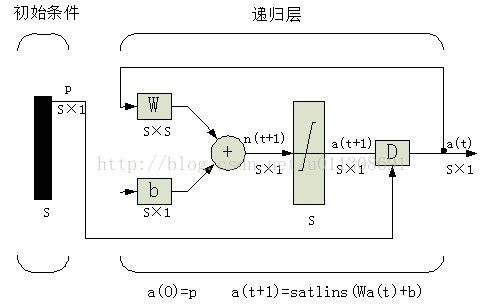
递归网络 一个递归网络是一个带反馈的网络,其部分输出连接到它的输入。图2-13给出了一种类型的离散时间递归网络。
如何选取一种网络结构
应用问题的描述从如下几个方面非常有助于定义网络的结构:
1)网络的输入个数=应用问题的输入数;
2)输出层神经元的数目=应用问题的输出数目;
3)输出层的传输函数选择至少部分依赖与应用问题的输出描述。