算法导论之排序：快速排序、归并排序、计数排序、基数排序、桶排序

问题描述：

输入：一个n个数的序列<a1,a2,a3,a4,a5,……,an>。

输出：输入序列的一个排列<a1',a2',a3',a4',……,an'>。

相关知识：

关键字：排序问题中要排序的值。

卫星数据：与关键字一同存储的值，如map中的key和value。

快速排序：

快速排序在最坏情况下的时间复杂度为θ(n^2)，但是它的期望时间复杂度是θ(nlgn)，而且θ(nlgn)中隐含的常数因子非常小。并且快速排序是原址排序的。

分解：将数组A[p..r]划分为两个子数组A[p..q-1]和A[q+1..r]，使A[p..q-1]中元素都小于等于A[q]，而A[q]小于等于A[q+1..r]中的每一个元素。

解决：通过递归调用快速排序，对子数组A[p..q-1]和A[q+1..r]进行排序。

合并：因为子数组都是原址排序的，所以不需要合并操作。

代码的实现如下：

package algorithms;

import java.util.Random;

public class QuickSort {

	public QuickSort() {
	}

	public static void doQuickSort(int A[], int left, int right) {
		if (left >= right) {
			return;
		}
		int partition = doPartition(A, left, right);
		doQuickSort(A, left, partition - 1);
		doQuickSort(A, partition + 1, right);
		return;
	}

	private static int doPartition(int[] A, int left, int right) {
		int i = left - 1;
		int x = A[right];
		int temp;
		for (int j = left; j < right; j++) {
			if (A[j] <= x) {
				i++;
				if (i != j) {// 线程测试这里if对执行性能的影响
					temp = A[i];
					A[i] = A[j];
					A[j] = temp;
				}
			}
		}
		temp = A[i + 1];
		A[i + 1] = A[right];
		A[right] = temp;
		return i + 1;
	}

	public static void main(String[] args) throws InterruptedException {
		long start = System.currentTimeMillis();
		int[] A = new int[1000];
		Random random = new Random();
		for (int i = 0; i < 1000; i++) {
			A[i] = random.nextInt(1000);
		}
		doQuickSort(A, 0, A.length - 1);
		Thread t = new Thread(new Runnable() {

			@Override
			public void run() {
				System.out.println("this is test thread");

			}
		});
		t.start();
		Thread.sleep(100);
		t.join();
		long end = System.currentTimeMillis();
		System.out.println(end - start);

	}

}

快速排序的随机化：

与始终采用A[r]作为主元素的方法不同，随机抽样从子数组中随机选择一个元素作为主元。

对PARTITION和QUICKSORT的更改比较少，只需要随机生成一个主元就可以，代码如下：

private static int doRandomPartition(int[] A, int left, int right) {
		Random random = new Random();
		int i = left + random.nextInt(right-left);
		int temp = A[right];
		A[right]=A[i];
		A[i]=temp;
		return doPartition(A, left, right);
	}

然后QUICKSORT调用这个doRandomPartition函数。

快速排序的随机化版本的期望运行时间是O(nlgn)。

归并排序：

分解：分解步骤仅仅计算子数组的中间位置，需要常量的时间，因此为θ(1)。

解决：我们递归的求解两个规模均为n/2的子问题，将贡献2T(n/2)的时间。

合并：一个具有n个元素的子数组的MERGE过程需要θ(n)的时间。

可以推出时间复杂度的函数关系为：

		θ(1)				N=1
T(N)=
		2T(N/2)+θ(N)		N>1

根据主方法可以求得归并排序的时间复杂度是θ(nlgn)。实现的代码如下：

package algorithms;

public class MergeSort {

	public MergeSort() {
		// TODO Auto-generated constructor stub
	}
	
	public static void doMergeSortII(int[] A, int m, int n){
		if (m == n) {
			return ;
		}
		int mid = (m + n)/2;
		doMergeSortII(A, m, mid);
		doMergeSortII(A, mid+1, n);
		int index = mid + 1,mark = 0,i = m;
		int[] B = new int[n-m+1];
		while(i <= mid && index <= n) {
			if (A[i] > A[index])
				B[mark++] = A[index++];
			else 
				B[mark++] = A[i++];
		}
		while (i <= mid) {
			B[mark++]= A[i++];
		}
		while (index <= n) {
			B[mark++]= A[index++];
		}
		for (int j = 0; j < B.length; j++) {
			A[j+m]=B[j];
		}
		return ;
	}

	public static void main(String[] args) {
		int[] A = new int[]{0,9,8,7,6,5,4,3,2,1};
		doMergeSortII(A, 0, A.length-1);
		for (int i : A) {
			System.out.print(i + ",");
		}

	}

}

接下来是三种线性时间复杂度的排序算法：计数排序、基数排序、桶排序。这些算法不是通过比较来排序的。

计数排序：

基本思想：对每一个输入元素x，确定小于x的元素的个数。（假设数据都是属于一个小区间的整数）

利用这一信息，可以直接把x放到它在输出数组中的位置上。代码如下：

package algorithms;

import java.util.Random;

public class CountSort {

	public static void main(String[] args) {
		int A[]=new int[100];
		Random random = new Random();
		for (int i = 0; i < A.length; i++) {
			A[i]=random.nextInt(100);
		}
		int B[] = new int[A.length];
		doCountSort(A, B, A.length);
		for (int i : B) {
			System.out.print(i + "->");
		}

	}

	private static void doCountSort(int[] a, int[] b, int k) {
		int c[] = new int[k]; // c的长度受a中最大元素值的影响
		for (int i = 0; i < c.length; i++) {
			c[i] = 0;
		}
		for (int i = 0; i < a.length; i++) {
			c[a[i]] += 1;
		}
		for (int i = 1; i < c.length; i++) {
			c[i] += c[i - 1];
		}
		for (int i = a.length - 1; i >= 0; i--) {
			b[c[a[i]] - 1] = a[i];
			c[a[i]]--;
		}
		return;
		//计数排序用空间换时间
	}

}

计数排序的时间复杂度是θ(n+k)。并且是稳定排序。

基数排序：

从最低位开始进行排序，依次往前进一位。

基数排序的时间复杂度是θ(d*(n+k))。并且是稳定排序。

桶排序：

桶排序假设输入的数据服从均匀分布，平均情况下它的时间代价为O(n)。（假设输入是一个随机的过程产生的，该过程将元素均匀、独立地分布到[0,1]区间上）

桶排序需要一个临时的数组来存放链表（即桶），在实现上我用arraylist来替代了链表的一些操作。代码如下：

package algorithms;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.Random;

public class BuckerSort {

	public static void main(String[] args) {
		Random random = new Random();
		double A[] = new double[100];
		for (int i = 0; i < A.length; i++) {
			A[i] = random.nextInt(100) / 100.0;//自动转型为double
		}
		doBucketSort(A);

		for (double d : A) {
			System.out.println(d);
		}
	}

	private static void doBucketSort(double[] a) {
		node b[] = new node[50];
		for (int i = 0; i < b.length; i++) {
			b[i] = new node();
		}
		for (int i = 0; i < a.length; i++) {
			node temp = new node();
			temp.num = a[i];
			temp.next = b[(int) (50 * a[i])].next;
			b[(int) (50 * a[i])].next = temp;
		}
		int j = 0;
		for (int i = 0; i < b.length; i++) {
			node n = b[i].next;
			ArrayList<node> al = new ArrayList<>();
			while (n != null) {
				al.add(n);
				n = n.next;
			}
			Collections.sort(al, new comparenode());
			for (node node : al) {
				a[j] = node.num;
				j++;
			}
		}

	}

	static class node {
		node next = null;
		double num = 0;
	}

	static class comparenode implements Comparator<node> {

		@Override
		public int compare(node o1, node o2) {
			if (o1.num > o2.num) {
				return 1;
			}
			return -1;
		}

	}
}

桶排序的时间复杂度是 θ(n)。

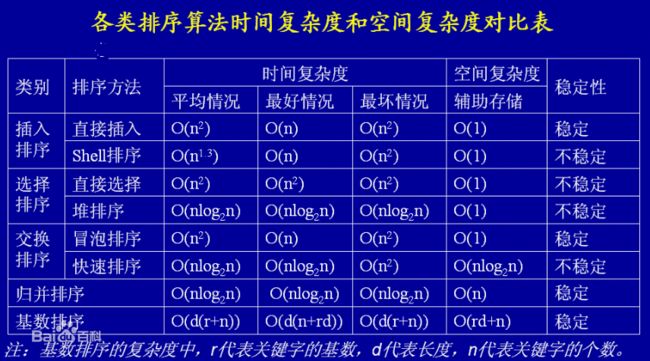
总结：

如下图：

下图来自百度百科