并查集 Ⅲ
[hdu 1198] (http://acm.hdu.edu.cn/showproblem.php?pid=1198)
题目描述:
Farm Irrigation
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7275 Accepted Submission(s): 3119
Problem Description
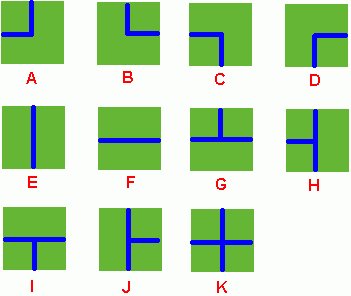
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.
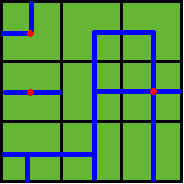
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.
Input
There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of ‘A’ to ‘K’, denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.
Output
For each test case, output in one line the least number of wellsprings needed.
Sample Input
2 2
DK
HF
3 3
ADC
FJK
IHE
-1 -1
Sample Output
2
3
分析:
此题要用并查集来处理,关键是把图形转化抽象为集合不容易想到,一旦能用一个11行4列的数组把每一块地和他们之间的关系表示出来之后,即可以把其转化为集合之间的关系,利用路径压缩和集合合并,把能连通的地放在同一个集合中,最后计算这样的集合有多少个,即为题目所问的需要建几口井。
代码实现和简要解析:
#include <iostream>
#include <stdio.h>
using namespace std;
char a[11][5]={"1010","1001","0110","0101","1100","0011","1011","1110","0111","1101","1111"};
int father[55][55];//用字符型的a数组来记录地上水管的分布情况,0和1分别表示每块地的上下左右分别不通水管和通水管
char map[55][55];//map字符数组用来存储输入的地的情况
int n,m;
int Find(int x)
{
if(father[x/n][x%n]!=x)
father[x/n][x%n]=Find(father[x/n][x%n]);
return father[x/n][x%n];
}
void Union(int x,int y)//合并x和y的集合
{
x=Find(x);
y=Find(y);
if(x!=y)
{
father[y/n][y%n]=x; } } void Judge(int i,int j)//判断map[i][j]和它的左侧和上侧是否连通,如果连通则使其合并
{
if(j>0&&a[map[i][j]-'A'][2]=='1'&&a[map[i][j-1]-'A'][3]=='1')//即为当前位置的左端有水管(为1)和当前位置左侧的右端(为1)有水管,即二者连通
Union(i*n+j,i*n+j-1);
if(i>0&&a[map[i][j]-'A'][0]=='1'&&a[map[i-1][j]-'A'][1]=='1')//当前位置的上端有水管并且当前位置的上侧的下端有水管,即为两者连通
Union(i*n+j,(i-1)*n+j);
}
int main()
{
int count;
while(scanf("%d%d",&m,&n)!=EOF)
{
if(n==-1&&m==-1)
break;
for(int i=0;i<m;i++)
{
scanf("%s",map[i]);
for(int j=0;j<n;j++)
{
father[i][j]=i*n+j;//将父亲节点初始化
}
}
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
Judge(i,j);
}
}
count=0;
for(int i=0;i<m;i++)//查找父亲节点是本身的个数,即形成连通集的个数
{
for(int j=0;j<n;j++)
{
if(father[i][j]==i*n+j)
{
count++;
}
}
}
printf("%d\n",count);
}
return 0;
}
对并查集的理解又深入了一步