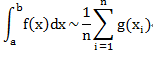受限玻尔兹曼机准备知识——MCMC方法和Gibbs采样

先点明几个叫法

MCMC方法：马尔可夫链-蒙特卡洛方法  (千万别叫成梅特罗波利斯蒙特卡罗方法了)

Metropolis-Hastings采样：梅特罗波利斯-哈斯廷斯采样

Gibbs采样：吉布斯采样

【题外话】：学一个东西，至少要知道英文翻译过来的中文名字叫啥，不然天天叫英文名字，哪天找教程遇到中文名字都不认识，比如BP神经网络，在网上搜搜，有几个把中文叫法说出来了，真是够折腾的，到底是叫反向传播网络，还是反馈神经网络，还是误差反向传递网络，对于稍微有点 强迫症的我是个坑。

还是介绍一下学习MCMC和Gibbs采样比较好的一个资料：随机采样方法与整理和受限玻尔兹曼机（RBM）学习笔记（一）预备知识(资料挺好的，本文就差不多是这两个个资料的精简版，主要围绕啊MCMC和Gibbs讲解)

蒙特卡洛方法

回忆一下前面一个文章蒙特卡洛方法，其中有一步骤就是用来计算积分的，转换成一个函数乘以一个概率密度函数。说过一句话“样本的容量足够大时，可以认为该事件的发生频率即为其概率”。当n足够大的时候，可以得到

也就是g(x)在p(x)分布上的均值。然后就可以用均值近似积分的值

其实不难发现

还是拿那个用一个圆和其外接正方形理解，就相当于，我们做了N次试验，每次试验都是丢一堆点到这个正方形包围区域，然后正方形内的点数(这个地方这样想比较方便：点构成面，那么我们就可以把正方形的面积想象成无数个点)也就是正方形近似的面积了，同理，被丢到圆内的点构成了圆的面积。回到那个用均值计算积分的累加式上，它就相当于我做了n次丢点的实验，所有的点构成了样本f(x)，而1/p(x)就代表了点落在圆内的概率大小。

【注】概率密度函数：表示瞬时值落在某指定范围内的概率，因此是幅值的函数，它随所取范围的幅值而变化。

马尔可夫链蒙特卡洛方法(MCMC方法)

前面已经介绍过关于HMM的相关知识了，主要就是分别用何种方法解决哪三种问题。马尔可夫链(通常我们说的就是一阶的情况)阐述的是事物发生的当前状态只与前面一个状态有关，比如明天天气状态只与今天的天气有关，与前天或者以前的天气状态无关。具体表述就是

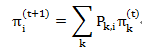代表的是第（t+1）时刻的状态为 i 的概率为它的前一时刻 t 的所有可能状态 k 乘以状态 k 到状态 i 的转移概率。

举个栗子哈~~还是天气的那个以明天的天气为起点，我们想预测后天的天气为晴的概率多大，我们需要知道明天的天气，但是明天天气有很多种可能，由初始概率可以知道明天天气分别为阴、晴、多云等的概率，然后分别乘以阴天到晴天的概率、晴天到晴天的转移概率、多云到晴天的转移概率等，然后相加就可以得到后天晴天的概率。在前面的文章有栗子，有需要可以去看看栗子就可以了。

然后出现了这样一个理论：当我们一直进行状态转移，到达一定次数的时候，这个状态发生的概率就会趋于稳定了，就比如，我们用天气一直预测，今天的比如晴天，我预测明天天气分别为阴、晴、多云的概率，然后用明天可能出现的天气情况预测后天的天气情况，然后我们一直计算，假如计算到达今年12月份最后一天的天气概率，就会发现这个概率跟12月份下旬的每天的天气概率情况差不多，差距很小。用数学的方法表示就是：

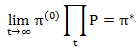代表的就是我们以初始状态的天气概率，不断的乘以这个转移矩阵(乘一次就是转移了一次，乘两次就是转移了两次)，当乘的次数越来越多的时候，概率变化会逐渐趋近与稳定。就像前面MC中说过的，我们不断的采样，最终的状态一定是一个稳定状态，最接近样本分布的状态。

上面这个情况称为马氏链定理：对于各态遍历的马尔可夫链(满足两个条件：非周期性，也就是状态转移不是按照某种规律循环，而是随机转移的；另一个条件是不可约，也就是每一个状态都可有其它任何一种状态转移过来，不可能存在一种状态转移的概率为0)，不管初始的概率如何取值，随着转移次数的增多，随机变量的取值分布最终会收敛于唯一的平稳分布。这个就是MCMC理论的基础。

现在的问题就是这个转移概率矩阵去怎么选择，让我们的初始状态沿着马尔可夫链按照这个转移概率矩阵去转移，最终得到的平稳分布正好是我们需要的概率分布。采样的时候，我们直接按照这个概率转移几次，达到我们需要的概率分布的时候，便去采样就可以了。随之便出现了下一个方法：梅特罗波利斯哈斯廷斯采样。

梅特罗波利斯哈斯廷斯采样

首先有一个概念需要知道叫做细致平稳条件：

如果非周期的马氏转移矩阵P和分布π(x)满足那么就成π(x)是马氏链的平稳分布。式子被称为细致平稳条件。也就是我们从状态 i 转移到状态 j 的时候损失的概率质量，刚好可以用从 j 到 i 状态转移增加的概率质量补回来。

但是这个细致平稳条件我们一般是达不到的。随后就有大牛想到加入了一个变量叫做转移提议分布Q（j；i）表示当前状态 i 提议转移到 j 状态，用它来建议下一步是个什么状态，然后用一个概率去接受它。就跟相亲一样，老爸老妈给你建议某个妹子的概率是多少，但是这还不够，你还得有一个接受她的概率才能和她结婚。

这个就是接受概率。到底接不接受呢？我们产生一个随机的[0,1] 范围的数，如果α 大于这个数就接受，小于就拒绝转移，保持原状态。

然后细指平稳条件就成了下面酱紫

然后推理一步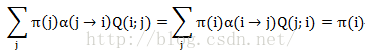，可以轻松发现，π(x)分布下的π(j)状态，经过转移，达到的状态依旧是满足π(x)分布，为π(i)。

所以梅特罗波利斯哈斯廷斯采样的精髓在于(自我感觉哈)，提出了一个转移提议分布，让细致平稳条件成为可能。此时新的转移矩阵为

那么问题又来了，这里面有一个随机数和接受概率的比较，两个东西都比较随机，造成了这种方法的不稳定性，如果接受概率一直灰常小，那么我每次都拒绝了，这状态还咋转移。于是，大牛又来了~~~

吉布斯采样（Gibbs采样）

条件概率的计算公式复习一下先

然后看一个比较有意思的式子推导

可以很清晰的发现，两个状态的相互转移概率其实是相等的，也就是满足细致平稳条件。也就是说，我们固定一个，按照x这个方向去转移状态，到达下一个状态，这个过程是满足细致平稳分布的。

用其它文章的话来说就是

这跟上面的梅特罗波利斯蒙特卡洛方法有什么关系呢？其实关键就在于，Gibbs规定了转移方向，在这个方向是，你的接受概率必须为1，其它方向必须为0，这便消除了随机性的影响。

最后再举一个栗子串一下，还是相亲的栗子。刚开始的时候是满世界找对象，世界上每个妹子在你面前出现的概率叫做初始概率，然后你再世界上行走去每个地方概率为转移概率，然后不断地走，走遍大江南北，世界各地，不断的转移状态，你就会发现，妹子们都是差不多一个样子，没啥区别，除了这种妹子就是那种妹子，这时候，妹子们的状态分布就会趋于一种平稳状态。除非你改变去每个地方的概率，或者世界上突然被外星人抓走了一堆妹子，这时候就会处于另一种稳态。这种就叫做马尔可夫链蒙特卡洛方法。

然后有的人就很聪明了，他想，我到处吓跑干啥，累死了，走遍各地，让妹子的分布达到稳态，这还不得老了。接着父母就开始忙活了，父母帮儿子找媳妇，父母每次给儿子按照某种提议分布去建议儿子娶这个，娶那个，儿子每看到一个妹子就以一定的接受概率去接受它，这种方法就是梅特罗波利斯哈斯廷斯采样。

最后，有人就发现，有些类型的妹子我非常喜欢，有些不喜欢，有些又有点拿捏不定，怎么办？这时候，我不想麻烦了，不喜欢和拿捏不定的，我统统不要，我就要一种风格的妹子，然后看到从样本中找到第一个这样风格的妹子，接下来按照这个风格，不断转移，找这种风格的妹子，当我找到数量足够的妹子(即Gibbs里面的n)，这时候我就得到了我喜欢的风格的妹子们了(期望的样本分布)。

好吧，如果有什么不对的，谢谢大家指正，我会不断完善的~~~~谢谢啦~~~