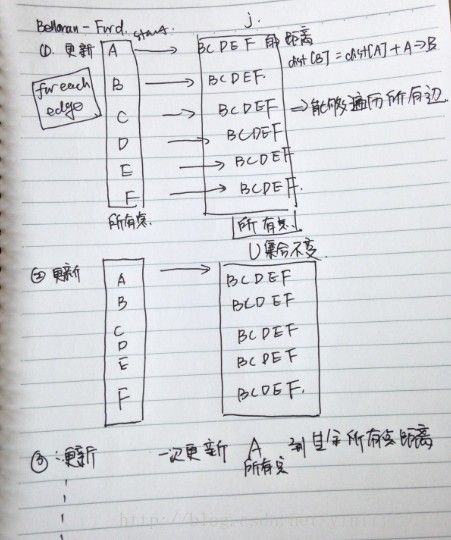
单源最短路径算法之Bellman-Ford算法

一、算法简介

    其实Bellman-Ford算法比Dijkstra算法更加简单，适用面更广，但是算法效率不如Dijkstra.

    Dijkstra算法是处理单源最短路径的有效算法，但它局限于边的权值非负的情况，若图中出现权值为负的边，Dijkstra算法就会失效，求出的最短路径就可能是错的。这时候，就需要使用其他的算法来求解最短路径，Bellman-Ford算法就是其中最常用的一个。该算法由美国数学家理查德•贝尔曼（Richard Bellman, 动态规划的提出者）和小莱斯特•福特（Lester Ford）发明。Bellman-Ford算法的流程如下：

一、Bellman-Ford与Dijkstra对比

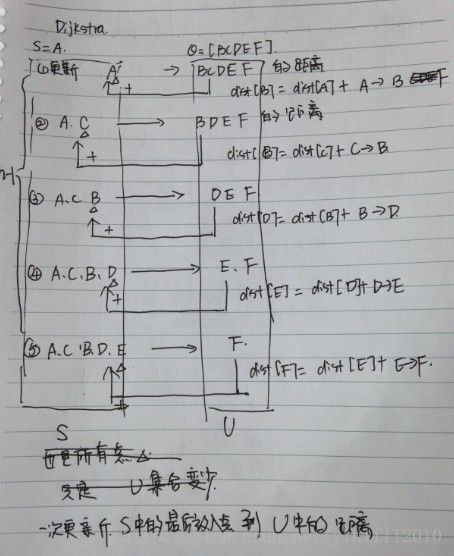
下面是修改前文Dijkstra算法得到的Bellman-Ford算法，可以看出Bellman更简单，但是效率更低

void Bellman_Ford(    
              const int numOfVertex,    /*节点数目*/    
              const int startVertex,    /*源节点*/    
              int (map)[][6],          /*有向图邻接矩阵*/    
              int *distance,            /*各个节点到达源节点的距离*/    
              int *prevVertex           /*各个节点的前一个节点*/    
              )    
{    
   // vector<bool> isInS;                 //是否已经在S集合中     
    //isInS.reserve(0);    
   // isInS.assign(numOfVertex, false);   //初始化，所有的节点都不在S集合中 ， 分配numOfVertex个字节   
        
    //step1  
 /*初始化distance和prevVertex数组*/    
    for(int i =0; i < numOfVertex; ++i)    
    {    
        distance[ i ] = map[ startVertex ][ i ];  //源节点到各个节点的距离，其中INT_MAX代表不可达  
        if(map[ startVertex ][ i ] < INT_MAX)  //如果是可达的  
            prevVertex[ i ] = startVertex;    
        else    
            prevVertex[ i ] = -1;       //表示还不知道前一个节点是什么     
    }    
    prevVertex[ startVertex ] = -1;  //源节点无前一个节点  
        
    /*开始使用贪心思想循环处理不在S集合中的每一个节点*/    
    //isInS[startVertex] = true;          //开始节点放入S集合中     
        
        
 int currentVertex = startVertex;  
        
    for (int i = 1; i < numOfVertex; i ++)      //这里循环从1开始是因为开始节点已经存放在S中了，还有numOfVertex-1个节点要处理     
    {    
        //step2    
        /*在Q中选择u到j的distance最小的一个节点， 如第一步A到C，最后目标到D*/     
       /* int minDistance = INT_MAX;    
        for(int j = 0; j < numOfVertex; ++j)  //  
        {    
            if((isInS[j] == false) && (distance[j] < minDistance))//寻找初始currentVertexA到Q中distance最小的节点 最后为新的currentVertexC    
            {    
                currentVertex = j;    
                minDistance = distance[j];    
            }    
        }    
        isInS[currentVertex] = true;//将这个节点currentVertex放入S集合中  * /   
            
         //step3  
        /*对这个新的currentVertexC做松弛计算，更新distance*/
		for(int start=0;start<numOfVertex;start++)
		{
			for (int j =0; j < numOfVertex; j ++)  
			{
				if (j!= startVertex  && map[start][j] < INT_MAX)  //在Q中，有距离的为c->d,c->e, c->b  
				{    
					int currentdist = distance[ start] + map[ start ][ j ];    
					if (currentdist < distance[ j ])  //distance[j = ]为开始到j的距离  
					{    
						distance[ j ] = currentdist;    
						prevVertex[ j ] = start;    
					}    
				}    
			} 
		}
    } 
	//判断是否存在环
	bool isLoopExist = false;
	for(int start=0;start<numOfVertex&& !isLoopExist;start++)
	{		
		for (int j =0; j < numOfVertex && !isLoopExist; j ++)  
		{    
            if (j!= startVertex  && map[start][j] < INT_MAX)  //在Q中，有距离的为c->d,c->e, c->b  
            {    
                int currentdist = distance[ start] + map[ start ][ j ];    
                if (currentdist < distance[ j ])  //distance[j = ]为开始到j的距离  
                {    
					isLoopExist = true;
                }    
			}    
		} 
	}
			if(!isLoopExist)
		{
			cout<<"no loop"<<endl;
		}
}

三、关于输出路径

1.可以使用栈，正如前文所示，还有可以使用递归输出

void printPath(int des)
{
    if(preVertex[des]!=-1) 
		printPath(preVertex[des]);
    cout<<des<<' ';

}

因为所有递归都可以转换为栈的操作

四、Bellman-Ford算法优化-SPFA

使用队列优先替换Bellman中的start循环，让每一次开始的仅仅是那些最有可能使结果更新的点

void SPFA(    
              const int numOfVertex,    /*节点数目*/    
              const int startVertex,    /*源节点*/    
              int (map)[][6],          /*有向图邻接矩阵*/    
              int *distance,            /*各个节点到达源节点的距离*/    
              int *prevVertex           /*各个节点的前一个节点*/    
              )    
{  
	//队列和判断ｉｎｄｅｘ是否在队列的结构
	queue<int> q;
	bool isInQueue[6];
    //step1  
 /*初始化distance和prevVertex数组*/    
    for(int i =0; i < numOfVertex; ++i)    
    {   
		isInQueue[i] = false;
        distance[ i ] = INT_MAX;  //这个距离必须初始化 为无穷大，否则加入队列的操作不好判断
        if(map[ startVertex ][ i ] < INT_MAX)  //如果是可达的  
            prevVertex[ i ] = startVertex;    
        else    
            prevVertex[ i ] = -1;       //表示还不知道前一个节点是什么     
    }    
    prevVertex[ startVertex ] = -1;  //源节点无前一个节点
	distance[startVertex]=0;

	q.push(startVertex);
	isInQueue[startVertex] = true;
        
    for (int i = 1; i < numOfVertex; i ++)      //这里循环从1开始是因为开始节点已经存放在S中了，还有numOfVertex-1个节点要处理     
    {    
		//for(int start=0;start<numOfVertex;start++)　Ｂｅｌｌｍａ－Ｆｏｒｄ中的使用所有的都循环，先在只循环那些最有可能达到最小解的
		//{
		 while(!q.empty()) 
		 {
			 int start = q.front();
			 cout<<"start"<<start<<endl;
			for (int j =0; j < numOfVertex; j ++)  
			{
				cout<<"start1"<<start<<endl;
				if (j!= startVertex  && map[start][j] < INT_MAX)  //在Q中，有距离的为c->d,c->e, c->b  
				{    
					int currentdist = distance[ start] + map[ start ][ j ];  
					if (currentdist < distance[ j ])  //distance[j = ]为开始到j的距离  
					{   
						distance[ j ] = currentdist;    
						prevVertex[ j ] = start;  
						if(!isInQueue[j])
						{
							q.push(j);
							isInQueue[j]= true;
						}
					}    
				}    
			}
			q.pop();
			isInQueue[start]= false;
		}
    } 
	//判断是否存在环
	bool isLoopExist = false;
	for(int start=0;start<numOfVertex&& !isLoopExist;start++)
	{		
		for (int j =0; j < numOfVertex && !isLoopExist; j ++)  
		{    
            if (j!= startVertex  && map[start][j] < INT_MAX)  //在Q中，有距离的为c->d,c->e, c->b  
            {    
                int currentdist = distance[ start] + map[ start ][ j ];    
                if (currentdist < distance[ j ])  //distance[j = ]为开始到j的距离  
                {    
					isLoopExist = true;
                }    
			}    
		} 
	}
			if(!isLoopExist)
		{
			cout<<"no loop"<<endl;
		}
}