HDU 3976 (高斯消元 KCL方程)

Electric resistance

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 498    Accepted Submission(s): 259

Problem Description

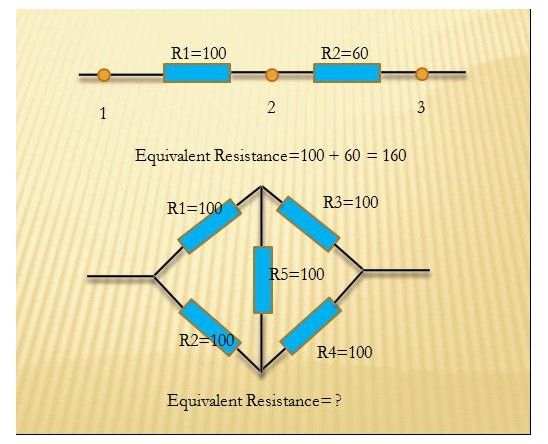
Now give you a circuit who has n nodes (marked from 1 to n) , please tell abcdxyzk the equivalent resistance of the circuit between node 1 and node n. You may assume that the circuit is connected. The equivalent resistance of the circuit between 1 and n is that, if you only consider node 1 as positive pole and node n as cathode , all the circuit could be regard as one resistance . (It's important to analyse complicated circuit ) At most one resistance will between any two nodes.

 

Input

In the first line has one integer T indicates the number of test cases. (T <= 100)

Each test first line contain two number n m(1<n<=50,0<m<=2000), n is the number of nodes, m is the number of resistances.Then follow m lines ,each line contains three integers a b c, which means there is one resistance between node a and node b whose resistance is c. (1 <= a,b<= n, 1<=c<=10^4) You may assume that any two nodes are connected!

 

Output

for each test output one line, print "Case #idx: " first where idx is the case number start from 1, the the equivalent resistance of the circuit between 1 and n. Please output the answer for 2 digital after the decimal point .

 

Sample Input

   
   
   
   

    
    
    
    1 
4 5 
1 2 1 
2 4 4 
1 3 8 
3 4 19 
2 3 12
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case #1: 4.21
   
   
   
   

 

真是个神题啊，给跪了～～深深地感受到了来自电路原理的恶意。

题意是给出电路上的n个点，然后m个电阻，告诉你每个电阻所在的左右两个点，求所有电阻的等效电阻。

根据基尔霍夫定律，流入或流出某一节点的所有之路的电流代数和为0。我们假设这些点是0-n-1并且0这个点的电势为0，那么只需要求出n-1这个点的电势。假设流入1的总电流是1A，那么等效电阻在数值上等于n-1这个点的电势。

然后根据基尔霍夫定律对每一个电阻更新KCL方程，x[i]表示i这个点的电势。

最后注意第一个点的电势是已知的，假设是0。因为我们无法求出每个点的绝对电势。如果忘记这一点KCL方程会跑出很奇怪的答案，因为解没有唯一性。

#include <bits/stdc++.h>
using namespace std;
#define maxn 111
#define eps 1e-9

double a[maxn][maxn], x[maxn];
int n, m;
int equ, var;

int Gauss () {
    int i, j, k, col, max_r;
    for (k = 0, col = 0; k < equ && col < var; k++, col++) {
        max_r = k;
        for (int i = k+1; i < equ; i++) { //找到最大的数所在的行
            if (fabs (a[i][col]) > fabs (a[max_r][col]))
                max_r = i;
        }
        if (k != max_r) { //交换行
            for (int j = col; j <= var; j++) {
                swap (a[k][j], a[max_r][j]);
            }
        }
        for (int i = k+1; i < equ; i++) { //消去
            if (a[i][col]) {
                double tmp = -a[i][col]/a[k][col];
                for (int j = col; j <= var; j++) {
                    a[i][j] += tmp*a[k][j];
                }
            }
        }
    }
    for (int i = equ-1; i >= 0; i--) { //回代
        double tmp = a[i][var];
        for (int j = i+1; j < var; j++) {
            tmp -= x[j]*a[i][j];
        }
        x[i] = tmp/a[i][i];
    }
    return 1;
}

int main () {
    //freopen ("in", "r", stdin);
    int kase = 0, t;
    cin >> t;
    while (t--) {
        cin >> n >> m;
        memset (a, 0, sizeof a);
        equ = n, var = n;
        a[0][var] = 1, a[n-1][var] = -1;
        for (int i = 1; i <= m; i++) {
            int u, v;
            double r;
            cin >> u >> v >>r; if (v < u) swap (u, v);
            u--, v--;
            a[u][u] -= 1.0/r;
            a[u][v] += 1.0/r;
            a[v][v] -= 1.0/r;
            a[v][u] += 1.0/r;
        }
        for (int i = 0; i < n; i++) {
            a[i][0] = 0;
        }
        Gauss ();
        printf ("Case #%d: %.2f\n", ++kase, x[n-1]);
    }
    return 0;
}