《图像局部不变性特征与描述》阅读笔记(1)-- 背景
1. 局部特征概念及性质
局部特征最重要是需要满足可重复性:同一场景在不同视角(几何变形)下,特征能保持自身的稳定(也就是不变性:令f为特征提取函数,t为某种几何变换,对于图像x,应有 f(t(x))=f(x))。此外,定义的局部特征应能在图像上检测到足够多的数量,然后通过阈值进行筛选。
2. 局部特征的发展
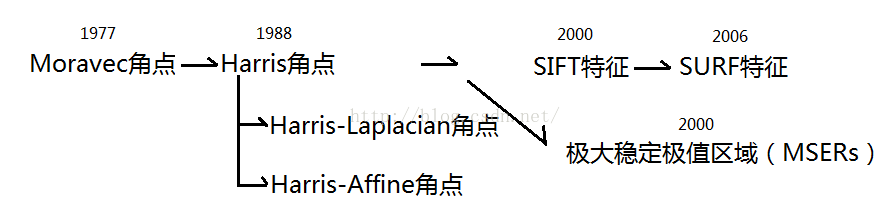
图2-1. 局部特征发展历程
Moravec角点考察当前点与其4-邻域(8-邻域)像素的相似性,只有当4(8)个方向的相似度都小于给定阈值才认为当前点为角点
算法步骤(参考http://blog.csdn.net/lu597203933/article/details/15027711):
1. 对每个点,计算E(u,v)。(u,v)取值为(1,0), (1,1), (0,1), (-1,1),代表4个方向
2. 选取E(u,v)最小的那个值(方向)作为备选(存在一个与原始图相同大小的矩阵M里)
3. 对M中的每个点,计算w窗口内取最大的那个值,如果该值大于阈值,则认为原始图中该坐标的点为特征点;之后M中的这个点平移w窗口大小的位置(与上个窗口不重叠),重复3(3中之所以在窗口内选最大值其实是起到了一定的筛选作用)
可以看到,因为只计算了4个方向(最多8个),因此当同一场景旋转一定角度后,之前能检测到的Moravec角点可能就检测不到了(因为不在这几个方向中)。也就是说,Moravec角点不具备旋转不变性,此外,其对噪声也很敏感。因此现在已经被淘汰。
Harris角点是Moravec角点的改进算法。针对Moravec角点对方向依赖性强,使用微分算子替代了窗口的移动;使用高斯窗口(模拟圆形窗口)替代Moravec的方形窗口,降低对噪声的敏感度;对E(见Moravec公式)变形为二次型,以区分边缘和角点。相对Moravec角点,Harris角点具备旋转不变性,具备平移不变性,但不具备空间尺度不变性(缩放)
Harris-Laplacian角点结合Harris和高斯尺度空间,使角点增加了空间尺度不变性。
Harris-Affine角点具有仿射不变性(仿射变换就是将某向量进行旋转、放缩和平移:x->Ax+b)
SIFT(Scale Invariant Feature Transform)特征利用金字塔和高斯滤波差分来快速求解高斯拉普拉斯空间中的极值点,能快速提取具有仿射不变性的特征点
SURF(Speeded Up Robust Feature)特征是SIFT的改进,通过积分图像和Harr小波进一步提高了检测速度
MSERs(Maximally Stable Extrernal Regions)特征借用分水岭的思路检测灰度最稳定的区域,然后对其进行旋转和尺度的归一化,具有严格的仿射不变性
从局部特征点的发展历程可以看到,局部特征的关注点集中在可重复性(各种不变性)。