bfs 2016.5.2
1、HDU 2612 Find a way
题意:
Y和M去KFC见面,有很多KFC,帮他们找一个KFC使得他们花费的时间总和最小
解题思路:
两次 bfs 分别找出他们到达他们都能到达的所有的KFC的最短时间
然后比较他们花费时间的和找出最小
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 200 + 5;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int dis[maxn][maxn][2];
int dir[][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int n, m;
struct Node {
int x, y;
int Count;
};
void bfs(int i, int j, int y_m);
int main()
{
// freopen("in.txt", "r", stdin);
while (cin>>n>>m) {
memset(dis, 0, sizeof(dis));
for (int i=0; i<n; ++i) {
for (int j=0; j<m; ++j) {
cin>>Map[i][j];
}
}
for (int i=0; i<n; ++i) {
for (int j=0; j<m; ++j) {
if (Map[i][j] == 'Y') {
memset(vis, false, sizeof(vis));
bfs(i, j, 0);
}
if (Map[i][j] == 'M') {
memset(vis, false, sizeof(vis));
bfs(i, j, 1);
}
}
}
int Min = INT_MAX;
for (int i=0; i<n; ++i) {
for (int j=0; j<m; ++j) {
if (Map[i][j] == '@') {
if (dis[i][j][0] > 0) {
int t = dis[i][j][0] + dis[i][j][1];
if (t < Min) {
Min = t;
}
}
}
}
}
cout<<Min*11<<endl;
}
return 0;
}
void bfs(int i, int j, int y_m)
{
Node node;
queue<Node> Queue;
node.x = i;
node.y = j;
node.Count = 0;
Queue.push(node);
vis[i][j] = true;
while (!Queue.empty()) {
int nx = Queue.front().x;
int ny = Queue.front().y;
int nCount = Queue.front().Count;
Queue.pop();
for (int i=0; i<4; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
node.Count = nCount + 1;
if ((node.x>=0) && (node.x<n) && (node.y>=0) && (node.y<m)) {
if (Map[node.x][node.y]!='#' && !vis[node.x][node.y]) {
Queue.push(node);
vis[node.x][node.y] = true;
dis[node.x][node.y][y_m] = node.Count;
}
}
}
}
}
2、POJ 2312 Battle City
题意:
你的坦克每次每次可以进行两种操作,向四周的空地移动或者射击砖墙将它变成空地但是不移动
问到达目的地需要的最少操作次数
解题思路:
关键是要保证队列中的操作次数是递增的
一:
可以将射击砖墙不移动这个操作 改为 把砖墙当作“伪空地”然后移动到这个地方,以后若遇到“伪空地”则变成空地然后直接跳出这一次循环
二、
优先队列
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 300 + 5;
int M, N;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int dir[][4] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
struct Node {
int x, y;
int Count;
};
int bfs(int a, int b);
int main()
{
// freopen("in.txt", "r", stdin);
while (cin>>M>>N && !(M==0&&N==0)) {
memset(vis, false, sizeof(vis));
int x, y;
for (int i=0; i<M; ++i) {
for (int j=0; j<N; ++j) {
cin>>Map[i][j];
if (Map[i][j] == 'Y') {
x = i;
y = j;
}
}
}
int least = bfs(x, y);
cout<<least<<endl;
}
return 0;
}
int bfs(int a, int b)
{
queue<Node> Queue;
Node node;
node.x = a;
node.y = b;
node.Count = 0;
Queue.push(node);
vis[a][b] = 1;
while (!Queue.empty()) {
int nx = Queue.front().x;
int ny = Queue.front().y;
int nCount = Queue.front().Count;
Queue.pop();
if (Map[nx][ny] == 'T') {
return nCount;
}
if (Map[nx][ny] == 'B') {
Map[nx][ny] = 'E';
node.x = nx;
node.y = ny;
node.Count = nCount + 1;
Queue.push(node);
continue;
}
for (int i=0; i<4; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
if (node.x>=0 && node.x<M && node.y>=0 && node.y<N) {
if (!vis[node.x][node.y] && (Map[node.x][node.y] != 'R' && Map[node.x][node.y] != 'S')) {
node.Count = nCount + 1;
vis[node.x][node.y] = 1;
Queue.push(node);
}
}
}
}
return -1;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 300 + 5;
int M, N;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int dir[][4] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
struct Node {
int x, y;
int Count;
bool operator < (const Node &p) const{
return p.Count < Count;
}
};
int bfs(int a, int b);
int main()
{
// freopen("in.txt", "r", stdin);
while (cin>>M>>N && !(M==0&&N==0)) {
memset(vis, false, sizeof(vis));
int x, y;
for (int i=0; i<M; ++i) {
for (int j=0; j<N; ++j) {
cin>>Map[i][j];
if (Map[i][j] == 'Y') {
x = i;
y = j;
}
}
}
int least = bfs(x, y);
cout<<least<<endl;
}
return 0;
}
int bfs(int a, int b)
{
priority_queue<Node> Queue;
Node node;
node.x = a;
node.y = b;
node.Count = 0;
Queue.push(node);
vis[a][b] = 1;
while (!Queue.empty()) {
int nx = Queue.top().x;
int ny = Queue.top().y;
int nCount = Queue.top().Count;
Queue.pop();
if (Map[nx][ny] == 'T') {
return nCount;
}
for (int i=0; i<4; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
if (node.x>=0 && node.x<M && node.y>=0 && node.y<N) {
if (!vis[node.x][node.y] && (Map[node.x][node.y] != 'R' && Map[node.x][node.y] != 'S')) {
if (Map[node.x][node.y] == 'B') {
node.Count = nCount + 2;
} else {
node.Count = nCount + 1;
}
vis[node.x][node.y] = 1;
Queue.push(node);
}
}
}
}
return -1;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 300 + 5;
int M, N;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int dir[][4] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
struct Node {
int x, y;
int Count;
friend bool operator < (const Node &a, const Node &b) {
return b.Count < a.Count;
}
};
int bfs(int a, int b);
int main()
{
// freopen("in.txt", "r", stdin);
while (cin>>M>>N && !(M==0&&N==0)) {
memset(vis, false, sizeof(vis));
int x, y;
for (int i=0; i<M; ++i) {
for (int j=0; j<N; ++j) {
cin>>Map[i][j];
if (Map[i][j] == 'Y') {
x = i;
y = j;
}
}
}
int least = bfs(x, y);
cout<<least<<endl;
}
return 0;
}
int bfs(int a, int b)
{
priority_queue<Node> Queue;
Node node;
node.x = a;
node.y = b;
node.Count = 0;
Queue.push(node);
vis[a][b] = 1;
while (!Queue.empty()) {
int nx = Queue.top().x;
int ny = Queue.top().y;
int nCount = Queue.top().Count;
Queue.pop();
if (Map[nx][ny] == 'T') {
return nCount;
}
for (int i=0; i<4; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
if (node.x>=0 && node.x<M && node.y>=0 && node.y<N) {
if (!vis[node.x][node.y] && (Map[node.x][node.y] != 'R' && Map[node.x][node.y] != 'S')) {
if (Map[node.x][node.y] == 'B') {
node.Count = nCount + 2;
} else {
node.Count = nCount + 1;
}
vis[node.x][node.y] = 1;
Queue.push(node);
}
}
}
}
return -1;
}
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 300 + 5;
int M, N;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int dir[][4] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
struct Node {
int x, y;
int Count;
};
bool operator < (const Node &a, const Node &b) {
return b.Count < a.Count;
}
int bfs(int a, int b);
int main()
{
// freopen("in.txt", "r", stdin);
while (cin>>M>>N && !(M==0&&N==0)) {
memset(vis, false, sizeof(vis));
int x, y;
for (int i=0; i<M; ++i) {
for (int j=0; j<N; ++j) {
cin>>Map[i][j];
if (Map[i][j] == 'Y') {
x = i;
y = j;
}
}
}
int least = bfs(x, y);
cout<<least<<endl;
}
return 0;
}
int bfs(int a, int b)
{
priority_queue<Node> Queue;
Node node;
node.x = a;
node.y = b;
node.Count = 0;
Queue.push(node);
vis[a][b] = 1;
while (!Queue.empty()) {
int nx = Queue.top().x;
int ny = Queue.top().y;
int nCount = Queue.top().Count;
Queue.pop();
if (Map[nx][ny] == 'T') {
return nCount;
}
for (int i=0; i<4; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
if (node.x>=0 && node.x<M && node.y>=0 && node.y<N) {
if (!vis[node.x][node.y] && (Map[node.x][node.y] != 'R' && Map[node.x][node.y] != 'S')) {
if (Map[node.x][node.y] == 'B') {
node.Count = nCount + 2;
} else {
node.Count = nCount + 1;
}
vis[node.x][node.y] = 1;
Queue.push(node);
}
}
}
}
return -1;
}
3、跳马问题
在中国象棋中,棋子活动的场所,叫做"棋盘",在长方形的平面上,绘有九条平行的竖线和十条平行横线相交组成,共九十个交叉点,棋子就摆在这些交叉点上。中间第五、第六两横线之间未画竖线的空白地带,称为"河界",整个棋盘就以"河界"分为相等的两部分;两方将帅坐镇、画有"米"字方格的地方,叫做"九宫"。
中国象棋中,马是威力很大的棋子。马走动的方法是一直一斜,即先横着或直着走一格,然后再斜着走一个对角线,俗称"马走斜"。马一次可走的选择点可以达到四周的八个点,故有"八面威风"之说。
我们约定最左下角点的坐标为(0,0),则最右上角的坐标为(9, 8)。上图中马在坐标(2, 2)处。它走一步可以到达坐标点(1, 0),(0, 1),(0, 3),(1, 4),(3, 4),(4, 3),(4, 1)或(3,0)。
我们约定当前棋盘上只有一个马,给出起点坐标和终点坐标,求从起点到终点,马最少要走几步?
Input
4个整数,前2个数表示起点坐标,后2个数表示终点坐标。
Output
一个整数,表示从起点到终点最少需要走的步数。
Sample Input
2 2 5 2
Sample Output
3
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
struct Node {
int x, y;
int steps;
};
const int maxn = 15;
bool vis[maxn][maxn];
int dir[][2] = {{-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}};
int x1, y1, x2, y2;
int bfs();
int main()
{
// freopen("in.txt", "r", stdin);
memset(vis, false, sizeof(vis));
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
x1 = 9-x1;
x2 = 9-x2;
printf("%d\n", bfs());
return 0;
}
int bfs()
{
Node node;
node.x = x1;
node.y = y1;
node.steps = 0;
vis[x1][y1] = true;
queue<Node> Queue;
Queue.push(node);
while (!Queue.empty()) {
int nx = Queue.front().x;
int ny = Queue.front().y;
int ns = Queue.front().steps;
if (nx == x2 && ny == y2) {
return ns;
}
Queue.pop();
for (int i=0; i<8; ++i) {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
node.steps = ns + 1;
if (0 <= node.x && node.x <= 9 && 0 <= node.y && node.y <= 8 && !vis[node.x][node.y]) {
vis[node.x][node.y] = true;
Queue.push(node);
}
}
}
return 0;
}
4、BJFU OJ 1548 大钉骑马走江湖
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
struct Node {
int x, y;
int step;
};
const int maxn = 100 + 5;
char Map[maxn][maxn];
bool vis[maxn][maxn];
int n, m;
int s_x, s_y, e_x, e_y;
int dir[][2] = {{-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}};
int flag[][2] = {{0, -1}, {-1, 0}, {-1, 0}, {0, 1}, {0, 1}, {1, 0}, {1, 0}, {0, -1}};
int bfs(void);
int main()
{
// freopen("in.txt", "r", stdin);
while (scanf("%d%d", &n, &m) != EOF) {
for (int i=0; i<n; ++i) {
for (int j=0; j<m; ++j) {
cin>>Map[i][j];
if (Map[i][j] == 's') {
s_x = i;
s_y = j;
} else if (Map[i][j] == 'e') {
e_x = i;
e_y = j;
}
}
}
printf("%d\n", bfs());
}
return 0;
}
int bfs(void)
{
memset(vis, false, sizeof(vis));
Node node;
node.x = s_x;
node.y = s_y;
node.step = 0;
vis[s_x][s_y] = true;
queue<Node> Queue;
Queue.push(node);
while (!Queue.empty()) {
int nx = Queue.front().x;
int ny = Queue.front().y;
int nstep = Queue.front().step;
if (nx == e_x && ny == e_y) {
return nstep;
}
Queue.pop();
for (int i=0; i<8; ++i) {
int a = nx + flag[i][0];
int b = ny + flag[i][1];
if (Map[a][b] == '.') {
node.x = nx + dir[i][0];
node.y = ny + dir[i][1];
node.step = nstep + 1;
if (node.x >= 0 && node.x <= n && node.y >=0 && node.y <= m && !vis[node.x][node.y] && Map[node.x][node.y] != '#') {
Queue.push(node);
vis[node.x][node.y] = true;
}
}
}
}
return -1;
}
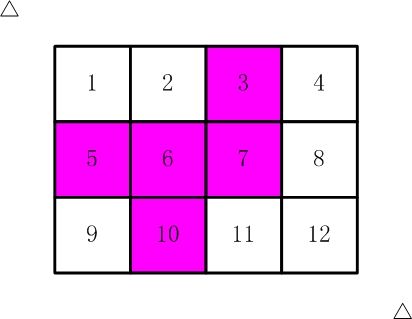
5、蓝桥杯2016省赛C语言B组7题 剪邮票
有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
比如,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
答案:
116
解题思路:
一:
选出5张不同邮票
规律:
(1)
某个邮票的上下左右可以分别用 -4 , +4 ,-1, +1 来表示
但要注意特殊情况,比如4、8、5、9
(2)
每个邮票至少和其它的一个邮票相连
假如将邮票a与邮票b相连的边与邮票b与邮票a相连的边看成是不同的
那么相连的边数应该 ≥ 8
二、
参考http://blog.csdn.net/u014552756/article/details/50946197
在原图中向上为-4,向下为+4,向左为-1,向右为+1,但是遇到4、8、5、9情况不符合
重构一下原图:
向上为-5,向下为+5,向左为-1,向右为+1
然后dfs判联通
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 12 + 5;
int num[maxn];
bool vis[maxn];
bool live[5];
int Count = 0;
int dir[4] = {-4, 4, -1 , 1};
bool check(void);
int main()
{
for (int i=1; i<=8; ++i) {
vis[i] = true;
num[0] = i;
for (int j=i+1; j<=9; ++j) {
vis[j] = true;
num[1] = j;
for (int k=j+1; k<=10; ++k) {
vis[k] = true;
num[2] = k;
for (int x=k+1; x<=11; ++x) {
vis[x] = true;
num[3] = x;
for (int y=x+1; y<=12; ++y) {
vis[y] = true;
num[4] = y;
memset(live, false, sizeof(live));
if (check()) {
++Count;
}
vis[y] = false;
}
vis[x] = false;
}
vis[k] = false;
}
vis[j] = false;
}
vis[i] = false;
}
cout<<Count<<endl;
return 0;
}
bool check(void)
{
int edge = 0;
for (int i=0; i<4; ++i) {
for (int j=0; j<5; ++j) {
if (!((num[j] == 4 || num[j] == 8) && i == 3) && !((num[j] == 5 || num[j] == 9) && i == 2)) {
if (vis[num[j] + dir[i]] == 1) {
edge++;
live[j] = true;
}
}
}
}
if (edge >= 8 && live[0] && live[1] && live[2] && live[3] && live[4]) {
return true;
}
return false;
}
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 12 + 5;
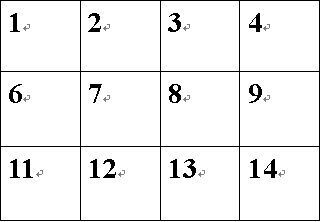
int Map[] = {1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14};
int num[maxn];
bool vis[maxn];
int Count = 0;
int dir[4] = {-5, 5, -1 , 1};
void dfs(int n);
int main()
{
for (int i=0; i<8; ++i) {
num[0] = Map[i];
for (int j=i+1; j<9; ++j) {
num[1] = Map[j];
for (int k=j+1; k<10; ++k) {
num[2] = Map[k];
for (int x=k+1; x<11; ++x) {
num[3] = Map[x];
for (int y=x+1; y<12; ++y) {
num[4] = Map[y];
memset(vis, false, sizeof(vis));
vis[0] = true;
dfs(0);
bool flag = true;
for (int a=0; a<5; ++a) {
if (!vis[a]) {
flag = false;
break;
}
}
if (flag) {
++Count;
}
}
}
}
}
}
cout<<Count<<endl;
return 0;
}
void dfs(int n)
{
for (int i=0; i<4; ++i) {
int t = num[n] + dir[i];
if (1 <= t && t <= 14 && t != 5 && t != 10) {
for (int j=0; j<5; ++j) {
if (!vis[j] && num[j] == t) {
vis[j] = true;
dfs(j);
}
}
}
}
}