2015 Astar Contest - Round 3 题解
1001 数长方形
题目大意
平面内有N条平行于坐标轴的线段,且不会在端点处相交
问共形成多少个矩形
算法思路
枚举4条线段的所有组合,分别作为矩形四条边,判断是否合法
时间复杂度: O(N4)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: A.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <complex>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
typedef complex<int> Point;
#define X real()
#define Y imag()
const int maxn = 25 + 5;
int n;
Point s[maxn], t[maxn];
bool o[maxn];
bool inter(int i, int j)
{
if (s[j].Y >= s[i].Y || t[j].Y <= s[i].Y) return false;
return s[i].X < s[j].X && s[j].X < t[i].X;
}
bool check(int d, int u, int l, int r)
{
if (!inter(d, l)) return false;
if (!inter(d, r)) return false;
if (!inter(u, l)) return false;
if (!inter(u, r)) return false;
return true;
}
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
rep(i,n) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
s[i] = Point(x1, y1);
t[i] = Point(x2, y2);
o[i] = (x1 == x2);
}
int res = 0;
rep(d,n) if (!o[d]) rep(u,n) if (u > d && !o[u]) {
rep(l,n) if (o[l]) rep(r,n) if (r > l && o[r]) {
if (check(d, u, l, r)) ++res;
}
}
printf("Case #%d:\n", ++cas);
printf("%d\n", res);
}
return 0;
}1002 弹吉他
题目大意
给出N个和弦需要按下的弦与品,每个和弦可以选择某种手势
序号大的手指所处的品位不能小于序号小的手指
移动某个手指的代价为曼哈顿距离,问依次弹出这N个和弦的最小代价
算法思路
DP,每个和弦最多有4!种手势
状态f[i][S]表示S对应的手势弹奏第i个和弦后,花费的最小代价
状态转移:f[i][S] = min{f[i-1][S0] + dis(S0, S)}
其中S可以直接存在4维数组中,注意检查手势是否合法
时间复杂度: O(N×4!2)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: B.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cstdlib>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
const int maxn = 5000 + 5;
int n;
Pii p[maxn][4];
int f[maxn][4][4][4][4];
bool check(int k, int y[])
{
rep(i,4) rep(j,4) if (j > i)
if (p[k][y[i]].second > p[k][y[j]].second) return false;
return true;
}
int dis(int i, int x, int y)
{
int dx = p[i][x].first - p[i+1][y].first;
int dy = p[i][x].second - p[i+1][y].second;
return abs(dx) + abs(dy);
}
int solve()
{
int x[4], y[4];
memset(f, 0x3f, sizeof(f));
f[0][0][1][2][3] = 0;
rep(i,n) {
rep(j,4) x[j] = j;
do {
int t = f[i][x[0]][x[1]][x[2]][x[3]];
if (t == inf) continue;
rep(j,4) y[j] = j;
do {
if (!check(i + 1, y)) continue;
int r = t;
rep(j,4) r += dis(i, x[j], y[j]);
int &res = f[i+1][y[0]][y[1]][y[2]][y[3]];
res = min(res, r);
} while (next_permutation(y , y + 4));
} while (next_permutation(x, x + 4));
}
int res = inf;
rep(j,4) x[j] = j;
do {
res = min(res, f[n][x[0]][x[1]][x[2]][x[3]]);
} while (next_permutation(x, x + 4));
return res;
}
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
rep(j,4) p[0][j] = Pii(0, j + 1);
For(i,1,n) rep(j,4)
scanf("%d%d", &p[i][j].first, &p[i][j].second);
printf("Case #%d:\n", ++cas);
printf("%d\n", solve());
}
return 0;
}1003 行路难
题目大意
给出一张有向图,边权为字符串,找出指定起点到终点,字典序最小的路径
如果不存在或长度为无穷,则输出”Tough way!”
算法思路
最短路,对于我的实现方法,需要从终点向起点松弛
因为如果从起点开始,对于某个字符串是另一个串前缀的情况,无法确定保留哪个
为了避免负环对spfa队列的影响,这里使用bellman-ford算法
- 当起点在n-1次松弛后被更新,则答案无限长
- 松弛6n次后起点答案不再变化
下面给出粗略的证明:
由于最短路上最多有n-1条边,所以n-1次松弛后,更新一定引入重边,由此可以构造负环
而如果最短路上不存在负环,则n-1条边构成的字符串最长为6(n-1)
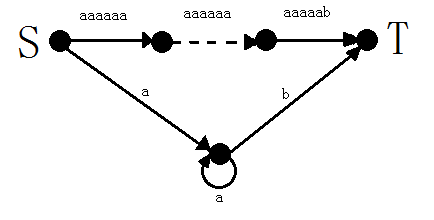
超过6n次松弛后,负环的长度肯定超过6(n-1),如果没有更新过起点,就再也不会更新了
至于为什么至少需要6n,可以参考下图
时间复杂度: O(VE)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: C.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
const int maxn = 50 + 5;
const int maxe = 500 + 5;
int psz;
struct Edge {
int u, v;
string w;
Edge *next;
} epool[maxe];
void add_edge(int u, int v, string w)
{
Edge *p = epool + psz++;
p->u = u; p->v = v; p->w = w;
}
int n, m, s, t;
string dis[maxn];
bool vis[maxn];
string bellman_ford()
{
int clk = 0;
memset(vis, false, sizeof(vis));
dis[t] = ""; vis[t] = true;
while (true) {
bool update = false;
for (Edge *i = epool; i < epool + psz; ++i) if (vis[i->v]) {
int u = i->u, v = i->v;
string tmp = i->w + dis[v];
if (!vis[u] || tmp < dis[u]) {
dis[u] = tmp;
update = vis[u] = true;
if (clk >= n - 1 && u == s) return "Tough way!";
}
}
if (!update || ++clk > n * 6) break;
}
return vis[s]? dis[s]: "Tough way!";
}
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
psz = 0;
scanf("%d%d%d%d", &n, &m, &s, &t);
while (m--) {
int u, v;
char buf[8];
scanf("%d%d%s", &u, &v, buf);
add_edge(u, v, buf);
}
printf("Case #%d:\n", ++cas);
puts(bellman_ford().c_str());
}
return 0;
}1004 蜀道难
题目大意
有N座山均匀分布在圆周上,相邻两座山之间的弧长为R,找出距离最远的两个山顶
其中山顶的距离为两座山的高度和,加上两座山沿圆弧的最短距离
算法思路
维护连续区间最值
将环复制一遍后变成链上的问题,不难发现,离某座山最远的山一定在它的前面的N/2座中
所以向右遍历每座山的同时,维护向前N/2宽度的区间内的最值,加上当前山的高度更新答案
而将当前高度H插入区间时,需要将区间内的值统一加上R
可以记录一个总的增量D,将H - D插入区间,再将D累加R
这样区间内的大小关系不变,而此时的最值只需要加上D,便可得到实际值
下面的代码中,使用了单调队列维护这一最值
时间复杂度: O(N)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: D.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
typedef pair<int, LL> Pil;
const int maxn = 100000 + 5;
int n, r, l;
int h[maxn*2];
struct Queue {
LL d;
deque<Pil> deq;
void clear() { d = 0; deq.clear(); }
void push(int i)
{
while (!deq.empty() && h[i] > deq.back().second + d)
deq.pop_back();
deq.push_back(Pii(i, h[i] - d)); d += r;
}
Pil query()
{
Pil res = deq.front(); res.second += d;
return res;
}
void pop(int i)
{
if (!deq.empty() && deq.front().first == i)
deq.pop_front();
}
} que;
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &r);
l = n / 2;
rep(i,n) scanf("%d", &h[i]), h[n+i] = h[i];
que.clear();
rep(i,l) que.push(i);
LL res = 0; Pii resp;
for (int i = l; i < 2 * n; ++i) {
LL v = que.query().second + h[i];
Pii p = Pii(i % n, que.query().first % n);
if (p.first > p.second) swap(p.first, p.second);
if (v > res) {
res = v; resp = p;
} else if (v == res) {
resp = min(resp, p);
}
que.pop(i - l);
que.push(i);
}
printf("Case #%d:\n", ++cas);
printf("%d %d\n", resp.first + 1, resp.second + 1);
}
return 0;
}1005 最强密码
题目大意
给出一个“密码生成串”
找到一个“最强密码”,不是这个“密码生成串”的子序列,并且长度最短
统计“最强密码”的个数
算法思路
DP
f[i]表示不是“原串以i结尾前缀”的子序列的最短字符串的长度
g[i]是上述字符串的个数
维护i前面每个字符最后出现的位置last[]
若存在未出现的字符,则
f[i] = 1
g[i] = 未出现的字符个数
否则
f[i] = min{f[last[j]]} + 1
g[i] = sum{g[last[j]] | f[[last[j]] + 1 == f[i]}
上式的含义为,i之前,以各个字母结尾的,长度为f[i]-1的密码串个数的累加
时间复杂度: O(26N)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: E.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
const int mod = 1000000007;
const int maxn = 100000 + 5;
int n;
char s[maxn];
int last[26];
int f[maxn], g[maxn];
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
scanf("%s", s);
n = strlen(s);
memset(last, -1, sizeof(last));
For(i,0,n) {
vector<int> vec;
rep(j,26) if (~last[j]) vec.push_back(last[j]);
if (i < n) last[s[i]-'a'] = i;
if (vec.size() < 26) {
f[i] = 1;
g[i] = 26 - vec.size();
} else {
int t = inf;
foreach(it,vec) t = min(t, f[*it]);
f[i] = t + 1;
g[i] = 0;
foreach(it,vec) if (f[*it] == t)
g[i] = (g[i] + g[*it]) % mod;
}
}
printf("Case #%d:\n", ++cas);
printf("%d %d\n", f[n], g[n]);
}
return 0;
}1006 平衡大师
题目大意
对一张N个点的有向图进行删边,使得每个点“入度减出度绝对值”的最大值最小
要求至少保留K条边
算法思路
费用流
先考虑最大流
对于有向图,存在总入度等于总出度这一性质,类比于网络流中的流量平衡
因此,从源点向入度大于出度的点连边,而入度小于出度的点连向汇点
由于要达到最大流,前者尽量向网络中流出,而后者则尽量从网络中流入
至于费用
如果给网络中每条边加上为1的费用,则通过网络的流量需要花费代价
回到本题,可以二分每个点“入度减出度绝对值”的最大值
对于不超过这个值的流量,可以建立一个临时节点,免费将流量流向此处,或从此处获取流量
而对于超出的部分,依然只能走网络中通过,带来的费用相当于需要删除的边
此时二分的判断条件为,删除等量于最大流最小费用的边后,是否还留有至少K条边
时间复杂度: O(logV×kVE)
代码
/** * Copyright © 2015 Authors. All rights reserved. * * FileName: F.cpp * Author: Beiyu Li <[email protected]> * Date: 2015-06-06 */
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <queue>
#include <map>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define For(i,s,t) for (int i = (s); i <= (t); ++i)
#define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
typedef long long LL;
typedef pair<int, int> Pii;
const int inf = 0x3f3f3f3f;
const LL infLL = 0x3f3f3f3f3f3f3f3fLL;
const int maxn = 50 + 5;
const int maxe = 10000 + 5;
class Cost_flow {
int n, psz;
struct Edge {
int u, v, r, c;
Edge *next, *cp;
} epool[maxe], *e[maxn];
int s, t, dist, cost;
int dis[maxn];
bool inq[maxn], vis[maxn];
bool modlable()
{
deque<int> deq;
memset(dis, 0x3f, sizeof(dis));
memset(inq, false, sizeof(inq));
dis[t] = 0; inq[t] = true; deq.push_back(t);
while (!deq.empty()) {
int u = deq.front(); deq.pop_front(); inq[u] = false;
for (Edge *i = e[u]; i; i = i->next) if (i->cp->r) {
int v = i->v;
if (dis[v] <= dis[u] - i->c) continue;
dis[v] = dis[u] - i->c;
if (inq[v]) continue; inq[v] = true;
deq.empty() || dis[v] < dis[deq.front()]?
deq.push_front(v): deq.push_back(v);
}
}
for (int u = 0; u < n; ++u)
for (Edge *i = e[u]; i; i = i->next)
i->c += dis[i->v] - dis[u];
dist += dis[s];
return dis[s] < inf;
}
int aug(int u, int m)
{
if (u == t) return cost += dist * m, m;
int f = 0; vis[u] = true;
for (Edge *i = e[u]; i; i = i->next) {
int v = i->v;
if (i->r && !i->c && !vis[v]) {
int d = aug(v, min(i->r, m));
i->r -= d; i->cp->r += d; m -= d; f += d;
if (!m) break;
}
}
return f;
}
public:
void init(int n)
{
this->n = n; psz = 0;
memset(e, 0, sizeof(e));
}
void add_edge(int u, int v, int w, int c)
{
Edge *i = epool + psz;
i->v = v; i->r = w; i->c = c; i->next = e[u]; e[u] = i;
i->cp = epool + (psz++ ^ 1);
if (psz & 1) add_edge(v, u, 0, -c);
}
int min_cost(int s, int t, int &flow)
{
this->s = s; this->t = t; dist = cost = flow = 0;
while (modlable()) {
int d;
do {
memset(vis, false, sizeof(vis));
flow += (d = aug(s, inf));
} while (d);
}
return cost;
}
} grp;
int n, m, k, tot;
int u[maxe], v[maxe], deg[maxn];
map<string, int> id;
int get_id(string s)
{
if (id.count(s)) return id[s];
return id[s] = tot++;
}
bool check(int c)
{
grp.init(n + 3);
int src = n, trg = n + 1, tmp = n + 2;
rep(i,m) grp.add_edge(u[i], v[i], 1, 1);
rep(i,n) {
if (deg[i] > 0) {
grp.add_edge(src, i, deg[i], 0);
grp.add_edge(i, tmp, c, 0);
}
if (deg[i] < 0) {
grp.add_edge(i, trg, -deg[i], 0);
grp.add_edge(tmp, i, c, 0);
}
}
return m - grp.min_cost(src, trg, tmp) >= k;
}
int main()
{
int T, cas = 0;
scanf("%d", &T);
while (T--) {
scanf("%d%d%d", &n, &m, &k);
tot = 0;
id.clear();
memset(deg, 0, sizeof(deg));
rep(i,m) {
char s[24];
scanf("%s", s);
u[i] = get_id(s);
scanf("%s", s);
v[i] = get_id(s);
++deg[u[i]], --deg[v[i]];
}
int l = 0, r = n;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
printf("Case #%d:\n", ++cas);
printf("%d\n", r);
}
return 0;
}