2014 Asia AnShan Regional Contest D题Galaxy(数学)(hdu5073)
Galaxy
Time Limit: 2000/1000 MS(Java/Others) Memory Limit: 262144/262144 K(Java/Others)
Total Submission(s): 2213 Accepted Submission(s): 534
Special Judge
Problem Description
Good news for us: to release the financial pressure, thegovernment started selling galaxies and we can buy them from now on! The firstone who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as apresent.
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy.There are n stars in Rho Galaxy, and they have the same weight, namely one unitweight, and a negligible volume. They initially lie in a line rotating aroundtheir center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates tooslow. As we know, to increase the angular speed with the same angular momentum,we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula
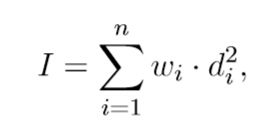
where wi is the weight of star i, di is thedistance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM createssome black holes and white holes so that he can transport stars in a negligibletime. After transportation, the n stars will also rotate around their newcenter of mass. Due to financial pressure, ATM can only transport at most kstars. Since volumes of the stars are negligible, two or more stars can betransported to the same position.
Now, you are supposed to calculate the minimum moment of inertia aftertransportation.
Input
The first linecontains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) andk(0 ≤ k ≤ n), as mentioned above. The next line contains n integersrepresenting the positions of the stars. The absolute values of positions will beno more than 50000.
Output
For each testcase, output one real number in one line representing the minimum moment ofinertia. Your answer will be considered correct if and only if its absolute orrelative error is less than 1e-9.
Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2
Sample Output
0
0.5
题意:n个点在一条直线上,移动k个点使得这n个点到质心的距离平方和最小。
思路:质心是物体(或由多个物体组成的系统)质量分布的中心,因为质量是相等的,所以这n个点的质心就是这n个点坐标和的平均数,x'=(x1+x2+...+xn)/n.
距离平方和s=(x1-x‘)^2+(x2-x')^2+...+(xn-x')^2.
展开得到s=∑xi^2-(∑xi)^2/n.
已经知道怎么求距离平方和了,剩下的就是移动点了。
很明显将k个点放到n-k个点的质心这k个点的距离平方和就不要求了。而且这k个点肯定就是n个点两端的点,所以我们维护一个连续n-k个数的和以及平方和,输出其中的最小值就行了。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<vector>
#include<queue>
#include<set>
#include<cmath>
#define INF 0xfffffff
#define MAX 1000000
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef __int64 ll;
ll a[50005];
int main()
{
int n,k;
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(int i=1; i<=n; i++)
scanf("%I64d",&a[i]);
int m=n-k;
if(m==0)
{
printf("0\n");
continue;
}
sort(a+1,a+n+1);
double s1=0;
double s2=0;
for(int i=1; i<=m; i++)//先移动后面的k个,求出剩下的和以及平方和
{
s1+=a[i];
s2+=a[i]*a[i];
}
double ans=s2-s1*s1/m;
for(int i=1,j=m+1; j<=n; i++,j++)//维护n-k的点个数
{
s1=s1-a[i]+a[j];
s2=s2-a[i]*a[i]+a[j]*a[j];
ans=min(ans,s2-s1*s1/m);
}
printf("%.1f\n",ans);
}
return 0;
}