hdu-2489 Minimal Ratio Tree(DFS+最小生成树)
题目链接:点击打开链接
Minimal Ratio Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 3909 Accepted Submission(s): 1203
Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
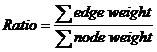
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
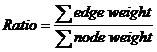
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
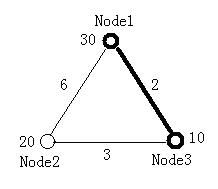
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .
Sample Input
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
Sample Output
1 3 1 2
题意:有n个点。接着输入n个点的权值,再输入图,代表了各条边的权值,题目说明了主对角线全为0,因此不用特别处理i==j的情况。
思路:n只有15, 想到用DFS全遍历,当然,裸DFS会TLE,于是只要加点剪枝就可以了。 31msAC。
这里剪枝的条件是1:第一个数+m<=n为什么呢? 假设n是5,m是3,那么第一个数至多是3吧(3,4,5),大于3就不行了
2:我们可以让序列严格递增,这样可以减少很少遍历,(同样几个数字,不剪枝会改变顺序出现很多次)
于是问题就简单了,题目要求m个点,每次我们遍历出符合条件的m个点时,其实m个点的权值就确定了,那么要让边和/点的权值结果最小,自然就是让边和最小了。
所以此时只要在这m个点求一次最小生成树得到最短长度就能得到一个题目要求的"最小比例树"了,然后再在所有符合条件的结果中取最小的,就是最终答案了~
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define N 20
#define INF 1<<30
#define eps 1e-8
int n,m;
double minn;
int ma[N][N];
int p[N],ans[N];
int f[N],flag[N];
int d[N],flag1[N];
int prim()
{
int ret=0;///最小生成树大小
memset(flag,0,sizeof(flag));
for(int i=1;i<m;i++)
d[i]=ma[f[0]][f[i]];
flag[0]=1;
for(int i=1;i<m;i++)
{
int v=-1;
for(int j=0;j<m;j++)
if(!flag[j]&&(v==-1||(d[v]>d[j])))
v=j;
if(v==-1)
return -1;
ret+=d[v];
flag[v]=1;
for(int j=0;j<m;j++)
if(!flag[j]&&d[j]>ma[f[v]][f[j]])
d[j]=ma[f[v]][f[j]];
}
return ret;
}
void dfs(int k)
{
if(k==m)
{
double sum=0;
for(int i=0;i<m;i++)
sum+=p[f[i]];
double ret=prim();
if(fabs(ret+1)<eps)
return;
if(minn-(ret/sum)>eps)
{
minn=ret/sum;
for(int i=0;i<m;i++)
ans[i]=f[i];
}
return;
}
for(int i=0;i<n;i++)
{
if(k==0&&i+m>n)
return;
if(k>0&&i<f[k-1])
continue;
if(!flag1[i])
{
flag1[i]=1;
f[k]=i;
dfs(k+1);
flag1[i]=0;
}
}
}
int main()
{
while(~scanf("%d %d",&n,&m)&&n)
{
for(int i=0;i<n;i++)
scanf("%d",&p[i]);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&ma[i][j]);
memset(flag1,0,sizeof(flag1));
minn=INF;
dfs(0);
for(int i=0;i<m-1;i++)
printf("%d ",ans[i]+1);
printf("%d\n",ans[m-1]+1);
}
return 0;
}