Codeforces Round #316 (Div. 2) D. Tree Requests(DFS序+BFS+二分)

题目链接：点这里

题意：

给你一棵树(n<=500000)，每个节点上有一个小写字母。

再给你m(m<=500000)个询问 v h，以v节点为根的子树下，深度为h的子节点集合能不能通过排序构成一个会回文串，能就输出Yes.不能就输出No.

= =看了别人的做法再看自己的做法，可能略显奇葩，不过觉得挺好理解的，我们来看下。

题解：

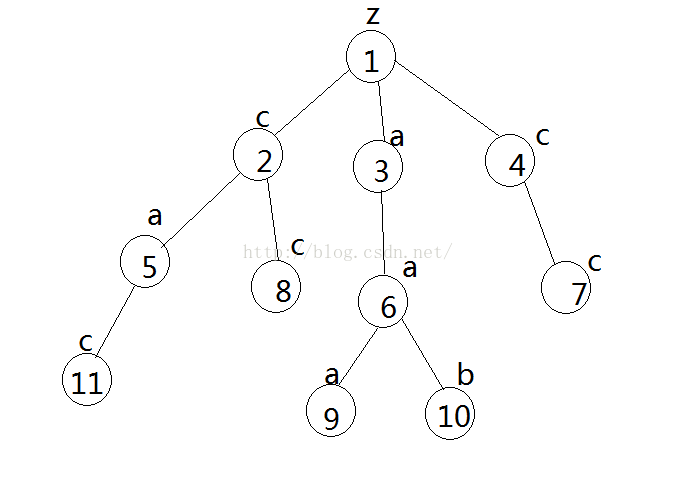
我们来看下例子。

如图：

1、我们首先得到dfs序为

2、我们再得到bfs序为

3、我们知道bfs序中相同深度的节点一定是连续的。

1   2 3 4   5 8 6 7   11 9 10

我们发现在相同深度下的dfs序也是递增的，而且也同深度相邻节点在bfs序上也是连续的。

然后我们可以知道每个节点作为根的子节点所管的区域（dfs序）

例如： 1->[2,7]  3->[6,10]

再结合同一深度的dfs序是递增的，就能知道以v为根深度h的子树下，利用二分在h深度的bfs序可以知道有哪些节点(注意边界)。

再利用前缀和加位运算就能得到答案。

详情看代码。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<sstream>
#include<algorithm>
#include<vector>
#include<bitset>
#include<set>
#include<queue>
#include<stack>
#include<map>
#include<cstdlib>
#include<cmath>
#define PI 2*asin(1.0)
#define LL long long
#define pb push_back
#define pa pair<int,int>
#define clr(a,b) memset(a,b,sizeof(a))
#define lson lr<<1,l,mid
#define rson lr<<1|1,mid+1,r
#define bug(x) printf("%d++++++++++++++++++++%d\n",x,x)
#define key_value ch[ch[root][1]][0]
const int  MOD = 1000000007;
const int N = 5e5 + 15;
const int maxn = 5e6+ 14;
const int letter = 130;
const int INF = 1e9;
const double pi=acos(-1.0);
const double eps=1e-8;
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int tot,n,m,head[N],deep[N],dfn[N],tottime;
int ll[N],rr[N],vs[N],vp[N];
int bfsll[N],bfsrr[N];
LL ans[N];
char a[N];
struct edges{
    int to,next;
}e[N];
void addedges(int u,int v){
    e[tot].to=v,e[tot].next=head[u],head[u]=tot++;
}
void dfs(int x,int f){
    deep[x]=f;
    ll[x]=++tottime;
    dfn[tottime]=x;
    for(int i=head[x];i!=-1;i=e[i].next){
        dfs(e[i].to,f+1);
    }
    rr[x]=tottime;
}
void bfs(){
    int to,x;
    queue<int>q;
    while(!q.empty()) q.pop();
    q.push(1);
    int num=0;
    while(!q.empty()){

        x=q.front();
        q.pop();
        vs[++num]=x;
        if(bfsll[deep[x]]==0) bfsrr[deep[x]]=bfsll[deep[x]]=num;
        else bfsrr[deep[x]]=num;
        for(int i=head[x];i!=-1;i=e[i].next) q.push(e[i].to);
    }
    for(int i=1;i<=n;i++) vp[i]=a[vs[i]],vs[i]=ll[vs[i]];
}
int main(){
    clr(head,-1),tot=0;
    int x,y;
    cin>>n>>m;
    for(int i=2;i<=n;i++){
        scanf("%d",&x);
        addedges(x,i);
    }
    scanf("%s",a+1);
    for(int i=1;i<=n;i++) a[i]=a[i]-'a';
    dfs(1,1);
    bfs();
    for(int i=1;i<=n;i++){
        ans[i]=ans[i-1]^(1<<vp[i]);
    }
    int ls,rs,lp,rp,llp,rrp,sum;
    while(m--){
        scanf("%d%d",&x,&y);
        ls=bfsll[y],rs=bfsrr[y];
        lp=ll[x],rp=rr[x];
            if(lp<=vs[ls]) llp=ls;
            else {
                int l=ls,r=rs,mid;
                int ans=ls-1;
                while(l<=r){
                    mid=(l+r)>>1;
                    if(vs[mid]>=lp) ans=mid,r=mid-1;
                    else l=mid+1;
                }
                llp=ans;
            }
            if(vs[rs]<=rp) rrp=rs;
            else {
                int l=ls,r=rs,mid;
                int ans=rs+1;
                while(l<=r){
                    mid=(l+r)>>1;
                    if(vs[mid]<=rp) ans=mid,l=mid+1;
                    else r=mid-1;
                }
                rrp=ans;
            }
            if(llp>rrp||llp<ls||llp>rs||rrp<ls||rrp>rs){
                puts("Yes");
                continue;
            }
            int ps=ans[rrp]^ans[llp-1];
            sum=0;
            while(ps){
                sum += (ps%2);
                ps/=2;
            }
            int len=rrp-llp+1;
            if(sum>1) puts("No");
            else puts("Yes");
    }
    return 0;
}