双调旅程(bitonic tour)问题
J.L. Bentley 建议通过只考虑双调旅程(bitonic tour)来简化TSP问题。,这种旅程即为从最左点开始,严格地从左到右直至最右点,然后严格地从右到左直至出发点。
双线性DP。
将一个人从最左端走到最右端,然后从最右端走到最左端等价成两个人同时从最左端不重复的走过中间的点并且到最右端。
我们不妨设这两个人为A和B,且总是假定走在前面的人是A。
再设函数dp(i, j)表示A走到i的位置,B走到j的位置,并且所有i,j之前的位置都被不重复的走过的最短距离之和。
由此得到递推公式:
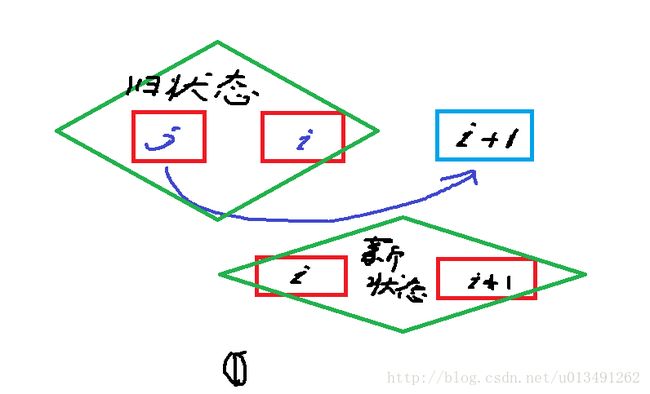
dp[i+1][i] = min(dp[i+1][i], dp[i][j] + distance(j, i+1));
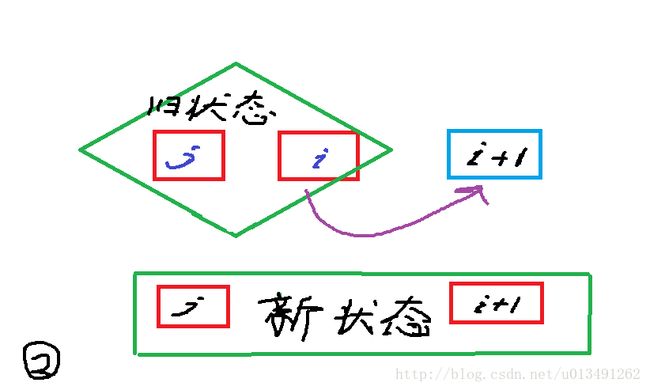
dp[i+1][j] = min(dp[i+1][j], dp[i][j] + distance(i, i+1));
由于最右节点必然是终点,所以走的快的人必然到达了n点,最终的距离就是枚举i,dp[n][i] + distance(i, n)中最小的。
http://poj.org/problem?id=2677
j < i , j 跳到i+1 。
j < i , i往右跳到 i+1。
const int Max_N = 208 ;
double dist[Max_N][Max_N] ;
double dp[Max_N][Max_N] ;
struct Point{
double x ;
double y ;
void read(){
scanf("%lf%lf" ,&x ,&y) ;
}
double Dist(Point &A){
return sqrt((x-A.x) * (x-A.x) + (y-A.y)*(y-A.y)) ;
}
}p[Max_N] ;
int N ;
double DP(){
int i , j ;
double ans = 1e10 ;
for(i = 2 ; i <= N ; i++){
for(j = i ; j <= N ; j++){
dist[i][j] = dist[j][i] = p[i].Dist(p[j]) ;
dp[i][j] = dp[j][i] = 1e10 ;
}
}
dp[2][1] = dist[2][1] ;
for(i = 1 ; i < N ; i++){
for(j = 1 ; j < i ; j++){
dp[i+1][i] = min(dp[i+1][i] , dp[i][j] + dist[j][i+1]) ;
dp[i+1][j] = min(dp[i+1][j] , dp[i][j] + dist[i][i+1]) ;
}
}
for(i = 1 ; i < N ; i++)
ans = min(ans , dp[N][i] + dist[i][N]) ;
return ans ;
}
int main(){
int i ;
while(cin>>N){
for(i = 1 ; i <= N ; i++)
p[i].read() ;
printf("%.2lf\n" ,DP()) ;
}
return 0 ;
}
ZOJ 2096
这个题目是Bitonic Tour的一个变种,将欧几里德平面的点变成了坐标轴上的点,因此距离函数dist由笛卡尔距离变成了坐标轴距离。
另外规则上也有一些变动,只需从左到走到最右,然后反过来从最右把左边所有没走过的走一下。
言下之意就是说起点不是固定的。我们不妨假设点的标号为1~n,这里我们虚拟一个起点0,
dist[0][i] = 0 ;
const int Max_N = 108 ;
int x[Max_N] ;
int dist[Max_N][Max_N] ;
int dp[Max_N][Max_N] ;
int N ;
inline int Abs(int x){
return x > 0 ? x : -x ;
}
int DP(){
int i , j ;
int ans = 1<<30 ;
for(i = 2 ; i <= N ; i++){
for(j = 2 ; j <= N ; j++){
dist[i][j] = dist[j][i] = Abs(x[i] - x[j]) ;
dp[i][j] = dp[j][i] = 1<<30 ;
}
}
for(i = 2 ; i <= N ; i++){
dist[1][i] = dist[i][1] = 0 ;
dp[1][i] = dp[i][1] = 1<<30 ;
}
dp[1][1] = 0 ;
dp[2][1] = dist[2][1] ;
for(i = 2 ; i < N ; i++){
for(j = 1 ; j < i ; j++){
dp[i+1][i] = min(dp[i+1][i] , dp[i][j] + dist[j][i+1]) ;
dp[i+1][j] = min(dp[i+1][j] , dp[i][j] + dist[i][i+1]) ;
}
}
for(i = 1 ; i < N ; i++)
ans = min(ans , dp[N][i] + dist[i][N]) ;
return ans ;
}
int main(){
int i ;
while(cin>>N && N){
N++ ;
for(i = 2 ; i <= N ; i++)
scanf("%d" ,&x[i]) ;
printf("%d\n" ,DP()) ;
}
return 0 ;
}
有很多从磁盘读取数据的需求,包括顺序读取、随机读取。为了提高效率,需要人为安排磁盘读取。然而,在现实中,这种做法很复杂。我们考虑一个相对简单的场景。
磁盘有许多轨道,每个轨道有许多扇区,用于存储数据。当我们想在特定扇区来读取数据时,磁头需要跳转到特定的轨道、具体扇区进行读取操作。为了简单,我们假设磁头可以在某个轨道顺时针或逆时针匀速旋转,旋转一周的时间是360个单位时间。磁头也可以随意移动到某个轨道进行读取,每跳转到一个相邻轨道的时间为400个单位时间,跳转前后磁头所在扇区位置不变。一次读取数据的时间为10个单位时间,读取前后磁头所在的扇区位置不变。磁头同时只能做一件事:跳转轨道,旋转或读取。
现在,需要在磁盘读取一组数据,假设每个轨道至多有一个读取请求,这个读取的扇区是轨道上分布在 0到359内的一个整数点扇区,即轨道的某个360等分点。磁头的起始点在0轨道0扇区,此时没有数据读取。在完成所有读取后,磁头需要回到0轨道0扇区的始点位置。请问完成给定的读取所需的最小时间。
Input
输入的第一行包含一个整数M(0<M<=100),表示测试数据的组数。
对于每组测试数据,第一行包含一个整数N(0<N<=1000),表示要读取的数据的数量。之后每行包含两个整数T和S(0<T<=1000,0<= S<360),表示每个数据的磁道和扇区,磁道是按升序排列,并且没有重复。
Output
对于每组测试数据,输出一个整数,表示完成全部读取所需的时间。
Sample Input
3
1
1 10
3
1 20
3 30
5 10
2
1 10
2 11
Sample Output
830
4090
1642
Source
2014年百度之星程序设计大赛 - 资格赛
const int maxn = 1008 ;
int x[maxn] , y[maxn] ;
int dp[maxn][maxn] ;
int N ;
int dist[maxn][maxn] ;
int getdist(int a , int b){
int t = (y[a] >= y[b])? (y[a] - y[b]) : (y[b] - y[a]) ;
return min(t , 360-t) ;
}
int DP(){
int i , j , ans = 100000000 ;
for(i = 1 ; i <= N ; i++){
for(j = i ; j <= N ; j++){
dist[i][j] = dist[j][i] = getdist(i , j) ;
dp[i][j] = dp[j][i] = 100000000 ;
}
}
dp[2][1] = dist[2][1] ;
for(i = 2 ; i < N ; i++){
for(j = 1 ; j < i ; j++){
dp[i+1][i] = min(dp[i+1][i] , dp[i][j] + dist[j][i+1]) ;
dp[i+1][j] = min(dp[i+1][j] , dp[i][j] + dist[i][i+1]) ;
}
}
for(i = 1 ; i < N ; i++)
ans = min(ans , dp[N][i] + dist[i][N]) ;
return ans ;
}
int main(){
int t , i , row , col , n , s ;
cin>>t ;
while(t--){
scanf("%d" ,&n) ;
N = n+1 ;
x[1] = y[1] = 0 ;
for(i = 2 ; i <= N ; i++){
scanf("%d%d" ,&x[i] , &y[i]) ;
}
s = x[N]*2*400 + 10*n ;
s += DP() ;
cout<< s << endl ;
}
return 0 ;
}