poj2513 Colored Sticks (欧拉通路+Trie树+并查集)
Description
Input
Output
Sample Input
blue red red violet cyan blue blue magenta magenta cyan
Sample Output
Possible
Hint
这道题的思路就是:判断是否是欧拉通路
那么怎么判断呢?
大家要知道欧拉通路的特点 1. 只有两个或者0个度为奇数的点 2.为一个集合
对于1我们可以用一个数组存贮顶点的度 对于2我们可以使用并查集 关键就在于我们如何把单词换成我们熟悉的整型变量来存贮
在这里有一种方法就是使用数据结构 Trie树 在博文的最下面有对Trie树的说明 在Trie树中每个单词的结尾附上ID 每次插入单词的时候如果
已经存在这个单词 直接返回ID 不存在的话 创建新节点 返回ID
并查集我就不说了。。判断集合个数 判断环个数 。。。现在还不学啊
附上ac代码:
#include <stdio.h>
struct Trie
{
int id;
Trie *word[26];
Trie()
{
id=0;
for(int i=0;i<26;i++)
word[i]=NULL;
}
};
int ID=1;
int degree[500000+10];
int fa[500000+10];
int find(int x)
{
if(fa[x]!=x) fa[x]=find(fa[x]);
return fa[x];
}
void init()
{
for(int i=0;i<250000+10;i++)
fa[i]=i;
}
int find_ID(Trie *root,char *str)
{
//判断这个单词是否存在于Trie树中
bool exit=true;
for(str;*str;str++)
{
if(!root->word[*str-'a'])
{
exit=false;
root->word[*str-'a']=new Trie();
}
root=root->word[*str-'a'];
}
//如果这个单词不存在 创建新的ID
if(!exit)
root->id=ID++;
return root->id;
}
int main()
{
char a[15],b[15];
init();
Trie *root=new Trie();
while(~scanf("%s %s",a,b))
{
int x=find_ID(root,a);
int y=find_ID(root,b);
int xx=find(x);
int yy=find(y);
if(xx!=yy)
fa[xx]=yy;
degree[x]++;
degree[y]++;
}
//度为奇数的顶点个数
int odd=0;
//是否为一个集合
int circle=0;
for(int i=1;i<ID;i++)
{
if(degree[i]%2==1)
odd++;
if(fa[i]==i)
circle++;
}
if(!(odd==0||odd==2)||circle>1)
{
puts("Impossible");
}
else
{
puts("Possible");
}
return 0;
}
知识拓展
提示一:Trie树的建立
小Hi于是在纸上画了一会,递给小Ho,道:“你看这棵树和这个词典有什么关系?”
小Ho盯着手里的纸想了一会道:“我知道了!对于从树的根节点走到每一个黑色节点所经过的路径,如果将路径上的字母都连起来的话,就都对应着词典中的一个单词呢!”
小Hi说道:“那你知道如何根据一个词典构建这样一棵树么?”
“不造!”
“想你也不知道,我来告诉你吧~”小Hi摆出一副老师的样子,说道:“你先这么想,如果我已经有了这样的一个词典和对应的一棵树,我要添加一个新的单词apart,我应该怎么做?”
“让我想想……”小Ho又开始苦思冥想:“首先我要先看看已经能走到哪一步了对吧?比如我从1号节点走"a"这一条边就可以走到2号节点,然后从2号节点走"p"这一条边可以走到3号节点,然后……就没路可走了!这时候我就需要添加一条从3号节点出发且标记为"p"的边才可以接着往下走……最后就是这样了!然后我把最后到达的这个结点标记为黑色就可以了。”
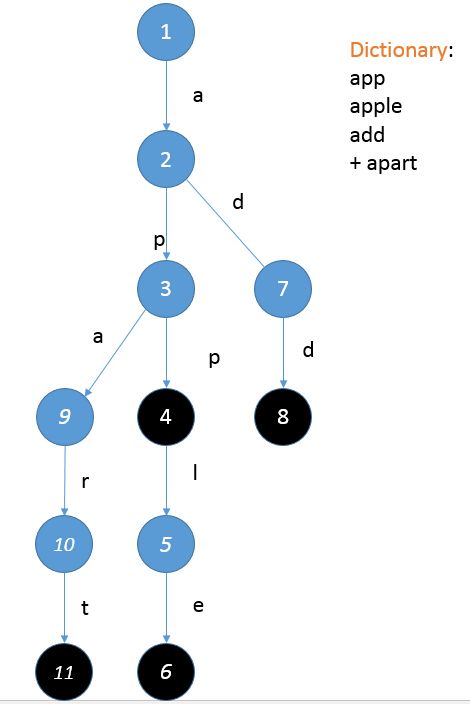
小Hi说道:“真聪明~那你不妨再算算如果是一个有10W个单词的词典,每个单词的长度不超过10的话,这棵树会有多大?”
小Ho于是掏出笔来,一边画一遍念叨:“假设我已经将前三个单词构成了这样一棵树,那么我要添加一个新的单词的时候,最坏情况是这个单词和之前的三个单词都没有公共前缀,那么这个新的单词的长度如果是5的话,我就至少要添加5个结点到树中才能够继续表示这个词典!”
“而如果每次都是最坏情况的话,这棵树最多也就100W个结点这么大!更何况最坏情况是不可能次次都发生的!毕竟字母表也才26个字母呢!”小Ho继续说道。
“嗯~这样我们是不是就可以用(单词个数*单词长度)个结点来表示一个词典了呢?小Hi问道。
“是的呢!”小Ho道:“但是这样一棵树又有什么用呢?”
“可别小看了它,它就是传说中的Trie树哦~至于他有什么用,一会你就知道了!”小Hi笑嘻嘻的回答道。
提示二:如何使用Trie树
“这个结点……是从根节点先走"a"然后走"p"到达的结点呢!哦~~我知道了,以这个结点为根的子树里所有标记结点都是以"ap"为前缀的单词呢!而且所有以"ap"为前缀的单词都在以这个节点为根的子树里~”小Ho惊喜道。
“是的呢~那你对怎么解决我的问题有想法了么?”小Hi追问道。
“唔...那就是每次拿到你的字符串之后,我在树上找到其对应的那个结点,然后统计这个节点中有多少个标记节点?”小Ho不是很确定的答道:“但是这样...似乎在最坏情况,也就是你每次给个字符串都很短的时候,我还是要扫描这棵树的很大一部分呢?也就是说虽然平均时间复杂度降低了,但是最坏情况时间复杂度还是很高的样子!”
小Hi笑嘻嘻道:”没想到你自己看出来了呢~我还以为又要教训你了!~那你有什么好的解决方法么?”
“没呢!小Hi你就别卖关子了,赶紧告诉我吧!”被折磨的够呛的小Ho开始求饶。
“好吧!就帮你这一回~”
提示三:在建立Trie树时同时进行统计!
Trie树 ,又称字典树或者前缀树,单词查找树,是一种树形结构。每个节点在书中的位置决定了它代表的字符串。
Trie可以看成是确定有限状态自动机的一种特例 它接受所有字典中出现的单词。根节点是起始态,所有粗线的节点都是接受态。
算法:
在Trie中插入 查找 删除一个字符串的操作相似。加入要插入的字符串为S,长度为m 我们以插入为例
(1)从根节点开始 从前向后依次读入S的每个字符c
(2)如果当前节点没有一条指向孩子的边为c 那么新建这样一条边和一个孩子节点
(3)沿着c这条边走到下一层的节点
(4)如果还有下一个字符 回到(1) 否则标记当前节点 结束。
Trie 就好像维护了一个字典 可以再这个字典里插入删除字符串 ,也可以查询一个字符串是否在字典中 Tir的插入查找删除复杂度都是O(m)的 其中m为待插入串的长度
用途:
1.Trie可以用来给字符串排序 把这些字符串都插入Trie之后 先序遍历即可
2.Trie的节点上可以存贮额外的信息 比如做词频统计 只需要每个节点上记录一个整数 每次插入时 将节点的计数器+1(也就是这道题)
3.Trie上支持查找最长公共前缀的字符串。
4.在一些应用中实现字符串的自动补全功能