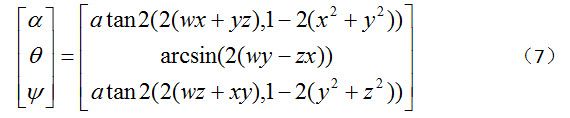四元数
对于四元数的概念也许大家不太熟悉,这里介绍下四元数概念,四元数、矩阵和欧拉角之间的关系,四元数球面插值的概念。这还是从当年写的本科毕业论文中摘录下来的,相当的没有技术含量。四元数的代码实现,见下载页面。
一. 四元数
1.1 四元数的概念
四元数是由爱尔兰数学家威廉•卢云•哈密顿在1843年发现的数学概念,在图形学中有重要的应用。在3D程序中,通常用四元数来计算3D物体的旋转角度,与矩阵相比,四元数更加高效,占用的储存空间更小,此外也更便于插值。 可以把四元数看做一个标量和一个3D向量的组合。实部w表示标量,虚部表示向量标记为V或三个单独的分量(x,y,z),则四元数可以记为[ w, V]或[ w,(x,y,z)]。正规化四元数可以表示为: 在三维中,可以用四元数表示绕着某个轴的旋转,如下公式所示:
在三维中,可以用四元数表示绕着某个轴的旋转,如下公式所示: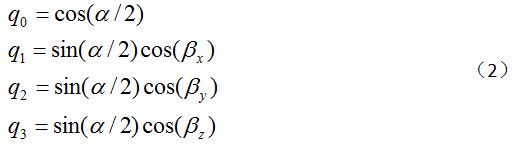
α表示旋转的角度,cos(βx), cos(βy) 和cos(βz)表示定位旋转轴的方向余弦
根据欧拉旋转定理,任何两个坐标系的相对定向,可以由一组四个数字来设定;其中三个数字是方向余弦,用来设定特征矢量(固定轴);第四个数字是绕着固定轴旋转的角值。这样四个数字的一组称为四元数。上面这段话阐述了四元数的原理:三维空间内所有的旋转都可以用四个数来表示。在通过四元数方法来计算旋转,已经替代了方向余弦方法,这是因为它能减少所需的工作,和它能减小舍入误差。在电脑图形学里,四元数与四元数之间,简易执行插值的能力是很有价值的。
1.2 旋转矩阵
旋转矩阵(Rotation Matrix)与一个向量相乘,会改变向量的方向但不改变大小的效果。旋转可分为主动旋转与被动旋转。主动旋转是指将向量逆时针围绕旋转轴所做出的旋转。被动旋转是对坐标轴本身进行的逆时针旋转,它相当于主动旋转的逆操作。在三维空间中,旋转矩阵有一个等于单位1的实特征值。只用三个实数就可以指定一个 3 维旋转矩阵。生成旋转矩阵的一种简单方式是把它作为三个基本旋转的序列复合。关于右手笛卡尔坐标系的 x-, y- 和 z-轴的旋转分别叫做 roll, pitch 和 yaw 旋转。因为这些旋转被表达为关于一个轴的旋转,它们的生成元很容易表达。
1.2 欧拉角
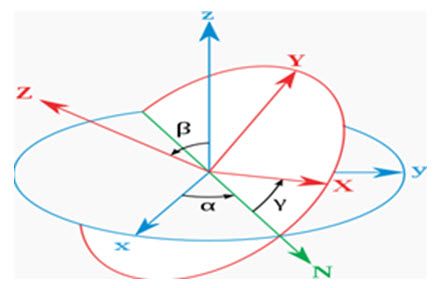
图1 欧拉角表示
设定 xyz-轴为参考系的参考轴,称 xy-平面与 XY-平面的相交为交点线,用英文字母(N)代表。zxz 顺规的欧拉角可以静态地这样定义:(1)a 是 x-轴与交点线的夹角;(2)B是 z-轴与Z-轴的夹角;(3)r 是交点线与X-轴的夹角。 欧拉角来描述刚体在三维欧几里得空间的取向,如图1所示。对于任何一个参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定。换句话说,任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的。而坐标系则固定于刚体,随着刚体的旋转而旋转。 设定刚体取向的旋转矩阵[R]是由三个基本旋转矩阵合成的,单独分开作用,每个矩阵各自代表绕着其转动轴的旋转。但是,当它们照次序相乘,最里面的(最右的) 矩阵代表绕着 z 轴的旋转,最外面的(最左的) 矩阵代表绕着 Z 轴的旋转,在中间的矩阵代表绕着交点线的旋转。
1.3 旋转矩阵、欧拉角和四元数之间的转化关系
旋转矩阵、欧拉角、四元数都可以表示三维空间模型的旋转,三者间也可以相互转化。正规化四元数q0+iq1+jq2+kq3可以用矩阵形式表示:(第1行1列的q2应该改成q3)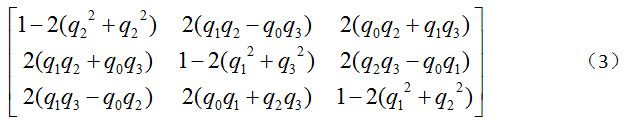 欧拉角也可转化成矩阵形式,欧拉角φ, θ, ψ表示的顺时针旋转可以用下面的矩阵形式表示:
欧拉角也可转化成矩阵形式,欧拉角φ, θ, ψ表示的顺时针旋转可以用下面的矩阵形式表示: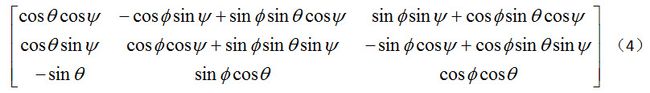 通过组合欧拉旋转(欧拉角分别是, θ, ψ)的四元数表达示,可以得到欧拉角到四元数的转化关系,如下面的公式所示:
通过组合欧拉旋转(欧拉角分别是, θ, ψ)的四元数表达示,可以得到欧拉角到四元数的转化关系,如下面的公式所示: 同时可以得到,四元数到欧拉角的转换关系,如下面的公式所示:
同时可以得到,四元数到欧拉角的转换关系,如下面的公式所示: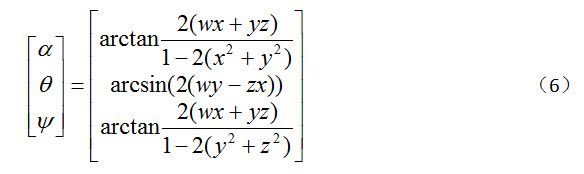
arctan和arcsin的结果是[-π/2,π/2],这并不能覆盖所有朝向,因此需要用atan2来代替arctan,从而产生所有可能的朝向,得到新的公式如下面所示:
1.4 线性插值与球面插值
在二维空间对向量进行线性插值,如图2所示,从而在向量间取得线性平滑的插值。得到等式P(t)=P0+(P1-P0)*t , 0 <= t <=1,通常还要将它标准化,转化为P(t)=P(t)/|P(t)|,这种方式的缺点便是在以 |P0| 为半径的圆的曲线轨迹上不是恒速变化的。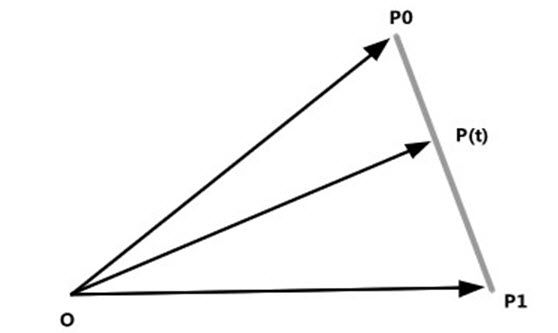
图2线性插值
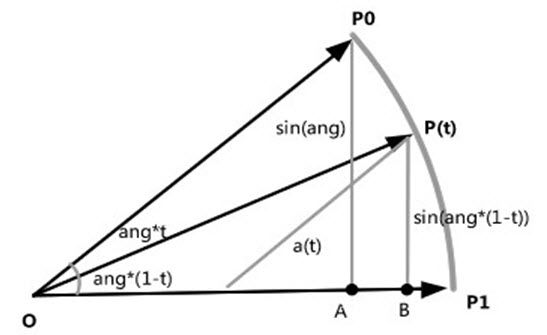
四元数在球面插值(Spherical Linear Interpolation)中仍只用于描述旋转,它是关于单位四元数构成的球表面上的操作,并且这一插值过程适用于在由三维向量升维构成的单位四元数中进行,所以基本上一次的插值过程可以降维到三维空间解释。其次,当向量仅发生旋转时,要求其起点向量到终点向量位于同一个二维空间,所以,球面插值本质上是处于二维空间的弧形插值。并且我们总是使用单位四元数来描述角度插值,因此在二维空间,被插值向量的长度是单位长度的,起始和终止向量以及由其长度为半径构成的圆中向量所夹的弧形便是我们观察的插值轨迹。 如图3球面插值所示,将 P(t) 分解为 P0 以及 P1 向量上的两个分量,根据平行四边形法则,我们首先观察在 P0 上的分量的长度 a(t),为了得到这个长度,作了 P0 末端到 A 以及 P(t) 末端到 B 的辅助线,根据相似三角形,各个边,得到比例关系a(t)/|P0|=sin(ang*(1-f))|P(t)|/(sin(ang)*|P0|),如果使用标准化的向量,简化为:a(t)=sin(ang*(1-f))/sin(ang)。使用同样的手段来计算另一个分量 b(t)=sin(ang*f)/sin(ang),最后得到这样的一组公式:P(t)=a(t)*P0+b(t)*P1。
图3 球面插值
二. 参考
【1】 http://en.wikipedia.org/wiki/Euler_angles
【2】 http://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
【3】 http://en.wikipedia.org/wiki/Quaternion