【线段树】hdu1828 & poj1177

补题解开始……

题目：

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter. 

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 



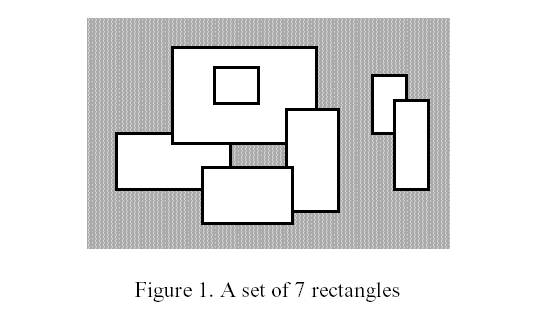
The corresponding boundary is the whole set of line segments drawn in Figure 2. 



The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate. 

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

   
   
   
   

    
    
    
    7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    228
   
   
   
   

 

还是扫描线法……

不过算面积并和算周长并是有区别的…………

算面积的时候重复的线段不用管，但是在计算周长的时候，重叠的线段会导致有错的

所以排序以后要用unique把重复的去掉才行

另外在扫描的过程中当前块的周长是等于

abs(tree[1].cnt - last) + (line[i + 1].x - line[i].x) * 2 * tree[1].num;

（画个图就理解了）

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
const long MAXN = 100010;
struct ty1
{
    int c, num;
    int cnt, lf, rf, lb, rb;
}tree[MAXN*3];     
struct ty
{
    int x, y1, y2;
    int f;
}line[MAXN];
int y[MAXN];
bool cmp(ty a, ty b)
{
    return a.x < b.x;
}     
void calc(int p, int l, int r)
{
    if(tree[p].c > 0)
    {
    	tree[p].num = 1;
        tree[p].cnt = tree[p].rf - tree[p].lf;
        tree[p].lb = tree[p].rb = 1;
        return;
    }    
    if(l + 1 == r)  {tree[p].cnt = tree[p].num = 0; tree[p].lb = tree[p].rb = 0;}
    else{
    	tree[p].cnt = tree[p * 2].cnt + tree[p * 2  + 1].cnt;
    	tree[p].num = tree[p * 2].num + tree[p * 2  + 1].num;
    	tree[p].lb = tree[p * 2].lb;
        tree[p].rb = tree[p * 2 + 1].rb;
    	if (tree[p * 2].rb && tree[p * 2 + 1].lb) tree[p].num--;
    }
}     
void build(int p,int l,int r)
{
    tree[p].cnt = tree[p].c = tree[p].num = 0;
    tree[p].lb = tree[p].rb = 0;
    tree[p].lf = y[l];
    tree[p].rf = y[r];
    if(l + 1 == r)  return;
    int mid = (l + r) >> 1;
    build(p * 2, l, mid);
    build(p * 2 + 1 ,mid, r);
}   
void change(int p, int l, int r, ty line)
{
	if(line.y1 == tree[p].lf && line.y2 == tree[p].rf)
    {
        tree[p].c += line.f;
        calc(p, l, r);
        return;
    }   
    int mid =(l + r) / 2; 
    if(line.y2 <= tree[p * 2].rf)  change(p * 2, l, mid, line);
    else if(line.y1 >= tree[p * 2 + 1].lf)  change(p * 2 + 1, mid, r, line);
    else{
    	ty tmp = line;
    	tmp.y2 = tree[p * 2].rf;
        change(p * 2, l, mid, tmp);
        tmp = line;
        tmp.y1 = tree[p * 2 + 1].lf;
        change(p * 2 + 1, mid, r, tmp);
    }
    calc(p, l, r);
}
int main()
{
    int n, m, t = 0;
    int x1, y1, x2, y2;
    while(scanf("%d",&n)!=EOF && n != 0)
    {
        m = 0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
            line[m].x = x1;
            line[m].y1 = y1;
            line[m].y2 = y2;
            line[m].f = 1;
            y[m] = y1;
            m++;
            line[m].x = x2;
            line[m].y1 = y1;
            line[m].y2 = y2;
            line[m].f = -1;
            y[m] = y2;
            m++;
        } 
		sort(line, line + m, cmp);
        sort(y, y + m);  
        int tmp = unique(y, y + m) - y;
        build(1, 0, tmp - 1);  
   
        int sum = 0, last = 0;
        for(int i = 0; i < m - 1; i++)
        {
        	change(1, 0, tmp - 1, line[i]);    
		    sum += abs(tree[1].cnt - last);	
		    sum += (line[i + 1].x - line[i].x) * 2 * tree[1].num;
		    //cout << abs(tree[1].cnt - last)	<< ' '<< tree[1].num << endl; 
			last = tree[1].cnt;     
        }    
        change(1, 0, tmp - 1, line[m - 1]);
        sum += abs(tree[1].cnt - last);
        printf("%d\n", sum);
    }    
    return 0;
}