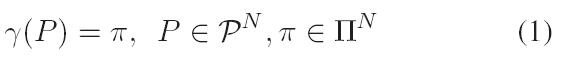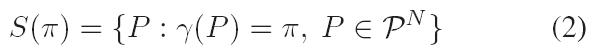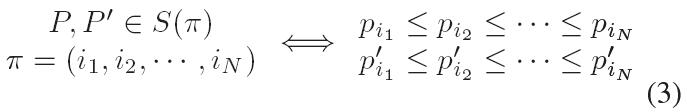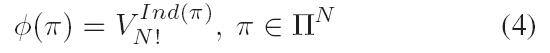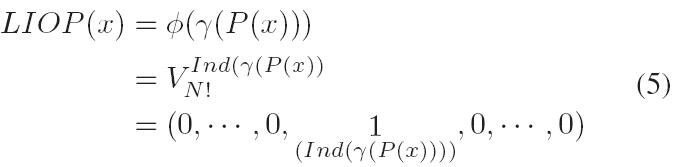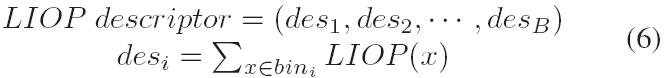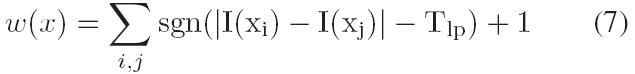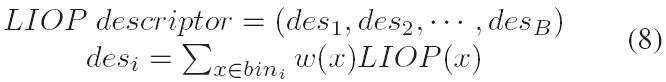【译文】Local Intensity Order Pattern for Feature Description
在上一篇文章【特征检测】LIOP特征描述算法中讲到了LIOP描述符，下面我将原文翻译如下，如有出入请以原文为准。
————————————————————————————————————————————————————————————————————————————————
译文：http://zhwang.me/publication/liop/index.html
局部强度顺序模型的特征描述
(Local Intensity Order Pattern for Feature Description)
摘要：
本文提出一种新的基于强度顺序的特征描述方法。具体来说，提出了一种局部强度顺序模型(LIOP)，对每个像素点的局部顺序信息进行编码，而整体顺序信息则是累加划分到每个子区域各自的LIOP值来得到。为了使局部块(local patch)的描述符具有很高辨识度，将采用本文提出的LIOP方法来提取局部和整体强度信息。研究表明，本文提出的描述符不仅具有单调强度变化不变性和旋转不变性，而且还对诸如视角变化、图像模糊和JEPG压缩等许多几何变换和光学变换具有较强的鲁棒性。通过对牛津大学提供的标准数据集(Oxford dataset)以及另外4组复杂光照变化图像的实验。结果表明，本文提出的描述符比现有最好的描述符性能上有重大的提升。
1 引言
图像局部特征广泛的应用于计算机视觉，比如目标识别 [13] ，纹理识别 [12] ，宽基线匹配 [24] ，图像检索 [18] ，全景图像拼接 [3] 。基本思路是，首先检测出感兴趣的点或区域，然后计算每个的不变性的特征描述符。一旦计算出特征描述符，就可以一些相似性度量方法如欧氏距离，来自动建立两幅不同图像之间特征的对应关系。许多 关于协变变换 ( 如：仿射变换 )， 这一类 检测感兴趣点或区域的方法被提出 。举例来说， Harris 角点 [10] 和 DoG (高斯差分) [13] 的兴趣点检测，还有 Harris-affine [15] ， Hessian-affin e[17] ， MSER (最大稳定极值区) [14] ， IBR (基于强度的区域)和 EBR (基于边缘的区域) [24] 等属于仿射协变区域检测。
关于特征描述符，在各种文献中也提出了许多方法。最广泛的是基于直方图的方法。例如，SIFT(尺度不变特征变换)[13]，GLOH(梯度位置-方向直方图)[16]以及DAISY[23]创建的梯度方向和位置直方图，旋转图像[12]创建的像素位置和强度直方图，还有形状上下文[2]创建的边缘点位置直方图等。这类基于直方图获得的描述符往往比其他方法得到的描述符具有更好的性能，比如基于滤波器[5,20]，基于导数[21]以及基于当下(moment-based descriptor)[6]等描述符。然而，虽然上面所提到的方法针对许多形变和扭曲具有完全或不完全的鲁棒性，但是它们不能处理更为复杂的照度变化，包括伽马校正，小镜面反射，曝光时间变化等。最近，为了解决复杂照度变化的问题，一些研究者提出使用(像素)强度顺序而不是原始(像素)强度作为特征描述符。Gupta和Mittal[8]提出一种新的特征描述，它是计算从检测区域选取的两个点之间翻转顺序之和的加权。Tang[22]创建2维直方图来计算序列分布及空间分布的编码。Heikkila[11]提出CS-LBP描述符，结合了SIFT描述符的强度和LBP[19]的纹理。Goswami[7]提出另一种基于LBP的方法，计算了环形区域上相邻两个像素的顺序信息。Gupta[9]提出一种更鲁棒的方法，它包含两个部分：强度相关性直方图和CS-LTP编码直方图。以上这些方法都对照度变化取得了良好的性能。
在本文中，我们提出一种基于强度顺序的特征描述新方法。该方法的基本原理是，当存在照度变化时，像素强度的相对顺序不会发生改变。为了有效的利用顺序信息，我们提出局部强度顺序模型(LIOP)，来对局部顺序信息进行编码，而整体顺序信息则是累加划分到每个子区域各自的LIOP值来得到。由于区域划分和LIOP计算是基于相对强度的，因此该描述符天生具有旋转不变性和单调的强度变化不变性。实验结果表明，对其他几何变换和光学变换如视角变化，图像模糊和JPEG压缩等也有一定的鲁棒性。
本文余下部分组织如下：第2节给出本文提出的方法的细节描述，第3节进行实验评估，第4节总结。
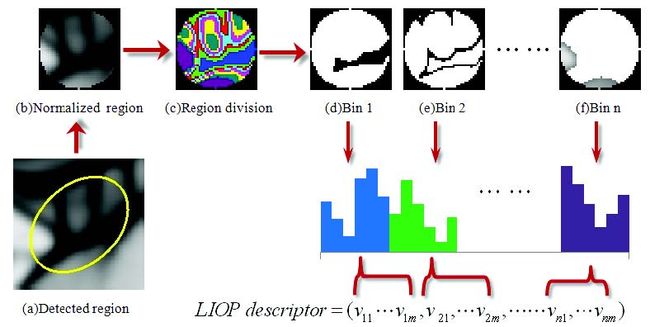
图1 本文方法流程
2 本文方法
本文对顺序信息使用一种新的方法来构造描述符。首先，整体强度顺序划分局部块为子块称为ordinal bins。然后，每个点的LIOP定义为相邻采样点的强度关系；LIOP描述符通过累加每个在ordinal bin的点的LIOP编码而被构造；最后，将它们连接起来。本文方法流程图见图1。
2.1 预处理，特征检测和归一化
首先，使用sigma为δp的高斯滤波器对图像进行平滑滤波，因为顺序关系对噪声敏感。其次，使用仿射协变区域检测器(如Harris-affine或Hessian-affine)来检测特征点的位置及估算其附近区域的仿射形状。再次，由于检测到的区域往往是不同大小和不同形状，将该区域归一化到一个固定直径的圆形区域中，以方便特征描述的统一处理。最后，再次使用sigma为δn的高斯滤波器来消除由于归一化步骤中插值操作带来的噪声。在本文中，将经过上述处理感兴趣区域称作局部块(local patch)。值得注意的是，与其他方法如文献[13,11,22,9]不同，本文方法没有根据局部一致性方向(如LOWE[13]建议的分配梯度方向)来旋转局部块，以实现旋转不变性。本文提出的描述符在旋转上是独立(不受限制)的，使其内在的就具有旋转不变性。有关细节的阐述，在下一节被提及。
2.2 区域划分
为了提高辨识度，使用基于直方图的方法将局部块划分成子块，通过创建每个子块的直方图来构造各自的描述符，然后将它们的描述符串联起来。此前，大多数的区域划分方法是基于空间位置的。例如，SIFT将空间位置量化到4x4的方格，GLOH使用划分为3个bins的径向及8个方向角度的对数坐标位置网格。这些方法的不足是需要估算每个局部块的局部一致性的方向，并且构造相对方位的描述符以实现旋转不变性。因此，这种描述符的性能严重依赖于精确的局部一致性方向的估算，这往往对噪声和畸变并不具有很好的鲁棒性[4,25]。为了避免估算局部一致性方向，将旋转图像[12]局部块划分成5个环状。然而，因为这仅仅在半径方向量化了空间位置，这使得其描述符的辨识度低于网格状的区域划分方法。
2.3 局部强度顺序模型描述符
用于特征描述的局部信息因方法而异。比如，旋转图像创建强度分布直方图，SIFT和GLOH创建梯度方向直方图。更近来说，基于局部二进制模式[19]的方法被提出，并比SIFT具有更高的性能。CS-LBP[11]创建具有中心对称的局部二进制模式直方图，CS-LTP[9]创建具有中心对称的三进制模式直方图。因为CS-LBP和CS-LTP仅仅比较中心对称的相邻采样点的强度，而并没有有效的利用中心对称的相邻采样点的强度关系。另外，还需要估算相邻采样点相对于局部一致性的方向，以实现旋转不变性，这使得方向的估算易出错误。为了克服这些问题，本文提出一种新局部强度顺序模型(LIOP)方法进行特征描述。该方法通过使用相邻采样点的强度顺序，从而有效的利用了局部信息。更重要的是，采用了旋转不变的采样方式避免了局部一致性方向的估算。因此，具有更高的辨识度。
2.3.1 LIOP的定义
在正式定义LIOP之前，先介绍一些映射函数或映射表。令
是N为矢量的集合，
是整数
所有可能的排列组合，映射
定义为一个P中N个元素的顺序组成的矢量
的一种排列组合
在排列组合表中的对应顺序。更具体的说，映射函数
将矢量P中的N个元素按照非降序排列
，使用下标列表
作为排列。为了避免出现歧义，定义
当且仅当
。从数学上讲，映射函数
定义为：
此处，
且
。
因此在
中共有N!(N的阶乘)种排列组合，映射函数
将
划分成N!个partitions(子集)，每个partitions对应唯一一种排列。对于排列组合
，
中与其对应的partitions为：
根据定义，存在以下等价关系：
也就是说，具有相同partitions的N维矢量，其对应的N个元素也具有相同的顺序关系，反之亦然。
中的集合可以根据与其一一对应的排列组合方式在
中的索引值进行编码。图2(d)表示了N=4的索引表。特征映射函数
定义为将排列
映射为N!维的特征矢量
，该矢量除了第i个位置为1外，其余元素都为0。
的数学定义为：
此处，
是
在索引表中的索引值，
。
根据以上的定义，令P(x)是一个N维的矢量，该矢量由局部块中x点的N邻域采样点的强度组成，则其LIOP可以定义为：
，且
记作第i个采样点
的强度。因此，总共有N!个不同的LIOP矢量，局部块被划分为N!个partitions，每个partitions用一个LIOP来表示。
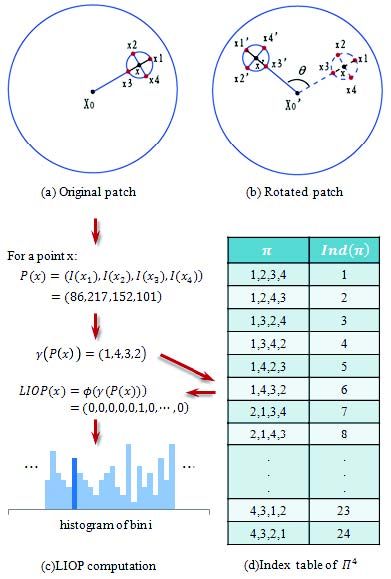
x点的N邻域采样均匀分布在以x为中心，R为半径的圆上。为了获得旋转不变性的采样，第一个点是沿着局部块的中心与点x的连线(径向)方向。因此在圆上会得到两个径向方向的点，其中离局部块中心最远的那个点当做采样的起始点(第1个点)。然后，剩余N-1个采样点则沿逆时针方向在圆上均匀采样。图2(a),(b)列举了一个N=4的旋转不变采样。可以看到，局部块点x与旋转后的局部块对应的点x’，它们4邻域的采样点分别是(x1,x2,x3,x4)，(x1’,x2’,x3’,x4’)。
2.3.2 构造描述符
在构造描述符时，分别累加每个ordinal bin内个点的LIOP，然后将它们连接起来。在图2中显示了构造LIOP描述符的过程。从数学上讲，局部块的LIOP描述符计算如下：
这里B是ordinal bin的个数，最终LIOP描述符是N! x B维的。
值得注意的是，LIOP描述符同时具有强度单调变化不变性和图像旋转不变性。建设x记作局部块中的一个点，x’记作点x经过强度单调变化和图像旋转后点，
和
分别是它们的N维矢量。因为我们采用了一个旋转不变的采样策略，则它们的强度顺序
和
具有相同的强度单调变化，根据公式3的等价关系，P(x)和P(x’)在
中的也对应相同的partition。换句话说，
。因此，根据公式5可以得到
。正如之前的讨论，基于区域划分的强度顺序是具有强度单调变化不变性和图像旋转不变性的。因此，点x和点x’属于同一个ordinal bin，这使得LIOP描述符不会发生改变。
由于高斯噪声的不同，相似强度比不相似的强度顺序更不稳定(也就是说像素值插值越小的越容易收到噪声影响)，具有不相似的邻域采样点个数越多的就会越稳定可靠，应该赋予更大的权值。本文提出一种权值函数来提高LIOP描述符的鲁棒性，定义如下：
这里sgn()表示符号函数，Tlp是预设的阈值。这种权值函数的措施是通过计算点x的邻域采样点不相似强度的个数来实现的。因此，描述符就变成了：
实验表明，这种权值方案比赋予相同权值或高斯权值的方法具有更好的性能(见图5)。
3.实验
3.1 数据集和评价标准
本文使用牛津数据集[1]来评价描述符。该数据集包含了结构和纹理场景不同的几何形变和光学变化。这六种不同的变化是：视角变化，尺度变化，图像旋转，图像模糊，照度变化及JPEG压缩。为了研究更多关于描述符在复杂光照变化的性能表现的细节，本文获取两组额外的图像’desktop’和’corridor’，它们都具有更为剧烈的照度变化(见图3)。本文通过对第二幅图像’desktop’的平方根和平方操作来 合成了两幅图像 。这种由非线性变化产生的单调强度变化。 图4 是两幅合成图像。
此处，
表示真实匹配的数目。
3.2 参数选择
本文方法中存在6个参数：1)区域检测之前的平滑参数δp. 2)区域归一化后的平滑参数δn. 3) ordinal bins的数量B. 4)邻域采样点个数N. 5)采样半径R. 6)权值函数的阈值Tlp。 使用Oxford数据集中的两幅图像(‘graf’和’wall’)来考察参数的影响。我们简单的尝试将所有这些参数组合起来，比较它们的匹配性能。由于篇幅有限，在图6中，仅仅给出了在1st和4th改变N(3和4)与B(4,6和8)的结果。可以看出，N=4比N=3得到更好的效果，B=8,6比B=4取得更好的效果。为了使得到的维度更小，本文选取B=6。因此，本文提出的LIOP描述符的维度为4! x 6=144。所有的参数选取如下表所示，并且在后序实验中保持不变。
同时，本文也比较了三种权重函数的性能：均匀权重，高斯权重，本文权重(公式7)。从图5中可以看出，本文提出的权值函数效果最好。
3.3 性能评价
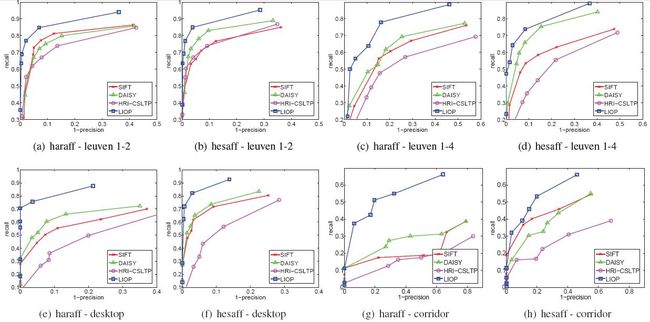
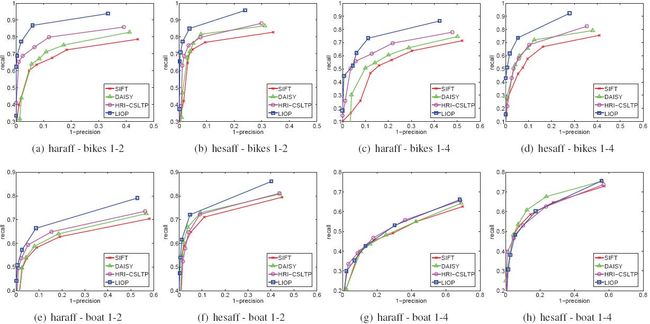
实验使用五种流行的仿射协变区域： Harris-affine(haraff) ， Hessian-affine(hesaff) ， MSER ， EBR 和 IBR 。根据结果，在不同的仿射区域，描述符的排名几乎保持不变 [16] 。由于篇幅限制，这里只给出 haraff 与 hesaff 区域，因为这二者比其他方法能够检测出更多的感兴趣区域。 Hesaff 检测类斑点结构而 haraff 检测类角点结构，二者都输出不同大小的椭圆区域。正如2.1的描述，这些椭圆区域被归一化到 固定大小 的圆形区域。正如文章 [16] ，为了公平的比较，使用相同直径( 41 个像素)。本文将LIOP描述符与SIFT[13]，DAISY[23]及HRI-CSLTP[9]进行对比，由于SIFT和DAISY是相当著名的高水准的描述符，而HRI-CSLTP是最近才提出的与类似于本文方法的基于顺序的方法。在实验中(Intel Core2 Quad CPU 2.83GHz)，构造特征描述符的平均时间是：2.1msfor SIFT，3.8msfor DAISY，5.3msfor HRI-CSLTP，5.5msfor LIOP。评价结果如图7，图8所示。对于Oxford数据集，本文只给出了两组图像(1st VS 2nd及1st VS 4th)对于每一种情况的结果，因为它们分别代表了小的和大的图像变化。
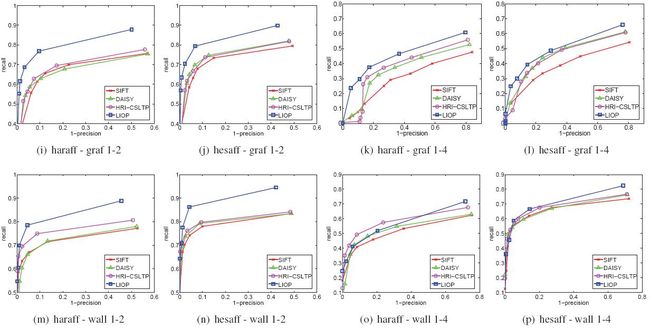
对于光照变化(见图7)，LIOP描述符比其他所有用于测试的描述符表现都好。由于是用来一种新的强度顺序，显著的提高了光照变化的性能。对于其他图像变化(见图8)，LIOP描述符在所有测试情况下也比SIFT好，在大多数测试情况下除了hesaff-boat1-4(图8(h))和haraff-wall1-4(图8(o))之外比DAISY和HRI-CSLTP。可以观察到，本文提出的LIOP描述符获得了高辨识度的同时也对许多图像保持鲁棒性。
4 结论
本文提出一种新的基于局部强度顺序模式(LIOP)的特征描述符。对比此前提出的基于强度顺序的描述符，LIOP在采样策略，比较规则和编码方式上有相当的不同。更具体的说，采用了一种旋转不变性的采样方式，并通过考虑所有采样点强度顺序的关系，全面的探究了局部强度的关系。同时，提出一种基于排列组合的编码方案来压缩特征矢量的维度，使得LIOP更适合于构造局部描述符。通过分别累加每个ordinal bin内每个点的LIOP，构造出完全基于相对强度的关系的描述符，使其具有图像旋转和单调强度不变性。实验结果表明，在各种各样的图像变化中，LIOP描述符比目前最高水准的描述符更为出色。
5 致谢
本项目受国家科学基金支持(60835003,61075038)。
参考文献
[1] http://www.robots.ox.ac.uk/~vgg/research/affine
[2] S. Belongie, J. Malik, and J. Puzicha. Shape matching and object recognition using shape contexts. PAMI, 24:509–522, 2002.
[3] M. Brown and D. G. Lowe. Automatic panoramic image stitching using invariant features. IJCV, 74:59–73, 2007.
[4] B. Fan, F. C. Wu, and Z. Y. Hu. Aggregating gradient distributions into intensity orders: A novel local image descriptor. In Proc. CVPR, pages 2377–2384, 2011.
[5] W. T. Freeman and E. H. Adelson. The design and use of steerable filters. PAMI, 13:891–906, 1991.
[6] L. J. V. Gool, T. Moons, and D. Ungureanu. Affine/ photometric invariants for planar intensity patterns. In Proc. ECCV, pages 642–651, 1996.
[7] B. Goswami, C. H. Chan, J. Kittler, and B. Christmas. Local ordinal contrast pattern histograms for spatiotemporal, lipbased speaker authentication. In Biometrics: Theory Applications and Systems (BTAS), pages 1–6, 2010.
[8] R. Gupta and A. Mittal. Smd: A locally stable monotonic change invariant feature descriptor. In Proc. ECCV, pages 265–277, 2008.
[9] R. Gupta, H. Patil, and A. Mittal. Robust order-based methods for feature description. In Proc. CVPR, pages 334 –341, 2010.
[10] C. Harris and M. Stephens. A combined corner and edge detection. In Proc. Alvey Vision Conference, pages 147–151, 1988.
[11] M. Heikkil¨a, M. Pietik¨ainen, and C. Schmid. Description of interest regions with local binary patterns. Pattern Recognition, 42:425–436, 2009.
[12] S. Lazebnik, C. Schmid, and J. Ponce. A sparse texture representation using local affine regions. PAMI, 27(8):1265 – 1278, 2005.
[13] D. G. Lowe. Distinctive image features from scale-invariant keypoints. IJCV, 60:91–110, 2004.
[14] J. Matas, O. Chum, U. Martin, and T. Pajdla. Robust wide baseline stereo from maximally stable extremal regions. In Proc. BMVC, volume 1, pages 384–393, 2002.
[15] K. Mikolajczyk and C. Schmid. Scale & affine invariant interest point detectors. IJCV, 60:63–86, 2004.
[16] K. Mikolajczyk and C. Schmid. A performance evaluation of local descriptors. PAMI, 27(10):1615 –1630, 2005.
[17] K. Mikolajczyk, T. Tuytelaars, C. Schmid, A. Zisserman, J. Matas, F. Schaffalitzky, T. Kadir, and L. V. Gool. A comparison of affine region detectors. IJCV, 65:43–72, 2005.
[18] D. Nister and H. Stewenius. Scalable recognition with a vocabulary tree. In Proc. CVPR, volume 2, pages 2161 – 2168, 2006.
[19] T. Ojala, M. Pietikainen, and T. Maenpaa. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. PAMI, 24:971–987, 2002.
[20] F. Schaffalitzky and A. Zisserman. Multi-view matching for unordered image sets, or ”how do i organize my holiday snaps?”. In Proc. ECCV, pages 414–431, 2002.
[21] C. Schmid and R. Mohr. Local grayvalue invariants for image retrieval. PAMI, 19:530–535, 1997.
[22] F. Tang, S. H. Lim, N. Chang, and H. Tao. A novel feature descriptor invariant to complex brightness changes. In Proc. CVPR, pages 2631 –2638, 2009.
[23] E. Tola, V. Lepetit, and P. Fua. Daisy: An efficient dense descriptor applied to wide-baseline stereo. PAMI, 32:815– 830, 2010.
[24] T. Tuytelaars and L. Van Gool. Matching widely separated views based on affine invariant regions. IJCV, 59:61–85, 2004.
[25] S. Winder and M. Brown. Learning local image descriptors. In Proc. CVPR, pages 1–8, 2007.
————————————————————————————————————————————————————————————————————————————————————
声明：
①本文翻译纯属兴趣，望思维共享，若有引用不当的地方，请联系博主；
②禁止任何商业行为。