树

普通树

树的实现:将每个节点的所有儿子都放在树节点的链表中.下面是典型的声明

typedef struct TreeNode *PtrToNode;
struct TreeNode
{
    ElementType Element;
    PtrToNode FirstChild;
    PtrToNode nextSibling;
}

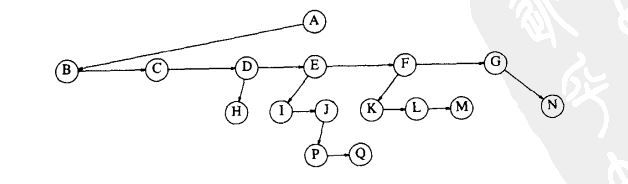
图中向下的箭头是指向FirstChild(第一个儿子)的指针.从左到右的箭头是指向NextSibling(下一兄弟)的指针.因为空指针太多.所以没有把它们画出.节点E有一个指针指向兄弟(F),另一个指针指向儿子(I),而有的节点这两种指针都没有.
树有很多应用.流行的用法之一是包括UNIX, VAX/VMS和DOS在内的许多常用操作系统中的目录结构.

二叉树

二叉树是一棵树,其中每个节点都不能有多于两个的儿子.

二叉树查找树

二叉树的一个重要的应用是它们在查找中的使用.
性质:对于树中的每个节点X,它的左子树中所有关键字值小于X的关键字值,而它的右子树中所有关键字值大于X的关键字值.

AVL树

一颗AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树.当向AVL树种插入一个节点时，可能会破坏AVL树的平衡，这时我们需要通过单旋转或双旋转来保持树的平衡

伸展树(splay tree)

它能在O(log n)内完成插入、查找和删除操作.splay tree是一种自调整形式的二叉查找树，了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法， 在每次查找之后对树进行重构，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

B-tree

多路搜索树，并不是二叉的。使用B-tree结构可以显著减少定位记录时所经历的中间过程，从而加快存取速度。按照翻译，B 通常认为是Balance的简称。这个数据结构一般用于数据库的索引，综合效率较高。
对于一棵m阶B-tree，每个结点至多可以拥有m个子结点。各结点的关键字和可以拥有的子结点数都有限制，规定m阶B-tree中，根结点至少有2个子结点，除非根结点为叶子节点，相应的，根结点中关键字的个数为1~m-1；非根结点至少有[m/2]（[]，向上取整）个子结点，相应的，关键字个数为[m/2]-1~m-1。
B-tree中，每个结点包含：
1、本结点所含关键字的个数；
2、指向父结点的指针；
3、关键字；
4、指向子结点的指针；

二叉查找树ADT

public class BinarySearchTree {
    // 树的根结点
    private TreeNode root = null;

    // 遍历结点列表
    private List<TreeNode> nodelist = new ArrayList<TreeNode>();

    //二叉查找树类
    private class TreeNode {

        private int key;
        private TreeNode leftChild;
        private TreeNode rightChild;
        private TreeNode parent;

        public TreeNode(int key, TreeNode leftChild, TreeNode rightChild,
                        TreeNode parent) {
            this.key = key;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
            this.parent = parent;
        }

        public int getKey() {
            return key;
        }

        public String toString() {
            String leftkey = (leftChild == null ? "" : String
                    .valueOf(leftChild.key));
            String rightkey = (rightChild == null ? "" : String
                    .valueOf(rightChild.key));
            return "(" + leftkey + " , " + key + " , " + rightkey + ")";
        }

    }
    /** * search: 在二叉查找树中查询给定关键字 * * @param key * 给定关键字 * @return 匹配给定关键字的树结点 */
    public TreeNode search(int key) {
        TreeNode pNode = root;
        while (pNode != null && pNode.key != key) {
            if (key < pNode.key) {
                pNode = pNode.leftChild;
            } else {
                pNode = pNode.rightChild;
            }
        }
        return pNode;
    }

    /** * insert: 将给定关键字插入到二叉查找树中 * * @param key * 给定关键字 */
    public void insert(int key) {
        TreeNode parentNode = null;
        TreeNode newNode = new TreeNode(key, null, null, null);
        TreeNode pNode = root;
        if (root == null) {
            root = newNode;
            return;
        }
        while (pNode != null) { //找到父节点
            parentNode = pNode;
            if (key < pNode.key) {
                pNode = pNode.leftChild;
            } else if (key > pNode.key) {
                pNode = pNode.rightChild;
            } else {
                // 树中已存在匹配给定关键字的结点，则什么都不做直接返回
                return;
            }
        }
        if (key < parentNode.key) {
            parentNode.leftChild = newNode;
            newNode.parent = parentNode;
        } else {
            parentNode.rightChild = newNode;
            newNode.parent = parentNode;
        }

    }

    /** * insert: 从二叉查找树中删除匹配给定关键字相应的树结点 * * @param key * 给定关键字 */
    public void delete(int key) throws Exception {
        TreeNode pNode = search(key);
        if (pNode == null) {
            throw new Exception("树中不存在要删除的关键字!");
        }
        delete(pNode);
    }

    /** * delete: 从二叉查找树中删除给定的结点. * * @param pNode * 要删除的结点 * * 前置条件： 给定结点在二叉查找树中已经存在 * @throws Exception */
    private void delete(TreeNode pNode) throws Exception {
        if (pNode == null) {
            return;
        }
        if (pNode.leftChild == null && pNode.rightChild == null) { // 该结点既无左孩子结点，也无右孩子结点
            TreeNode parentNode = pNode.parent;
            if (pNode == parentNode.leftChild) {
                parentNode.leftChild = null;
            } else {
                parentNode.rightChild = null;
            }
            return;
        }
        if (pNode.leftChild == null && pNode.rightChild != null) { // 该结点左孩子结点为空，右孩子结点非空
            TreeNode parentNode = pNode.parent;
            if (pNode == parentNode.leftChild) {
                parentNode.leftChild = pNode.rightChild;
                pNode.rightChild.parent = parentNode;
            } else {
                parentNode.rightChild = pNode.rightChild;
                pNode.rightChild.parent = parentNode;
            }
            return;
        }
        if (pNode.leftChild != null && pNode.rightChild == null) { // 该结点左孩子结点非空，右孩子结点为空
            TreeNode parentNode = pNode.parent;
            if (pNode == parentNode.leftChild) {
                parentNode.leftChild = pNode.leftChild;
                pNode.rightChild.parent = parentNode;
            } else {
                parentNode.rightChild = pNode.leftChild;
                pNode.rightChild.parent = parentNode;
            }
            return;
        }
        // 该结点左右孩子结点均非空，则删除该结点的后继结点，并用该后继结点取代该结点
        TreeNode successorNode = successor(pNode);
        delete(successorNode);
        pNode.key = successorNode.key;
    }

    /** * successor: 获取给定结点在中序遍历顺序下的后继结点 * * @param node * 给定树中的结点 * @return 若该结点存在中序遍历顺序下的后继结点，则返回其后继结点；否则返回 null * @throws Exception */
    public TreeNode successor(TreeNode node) throws Exception {
        if (node == null) {
            return null;
        }

        // 若该结点的右子树不为空，则其后继结点就是右子树中的最小关键字结点
        if (node.rightChild != null) {
            return minElemNode(node.rightChild);
        }
        // 若该结点右子树为空 (中序遍历下的后继结点)
        TreeNode parentNode = node.parent;
        while (parentNode != null && node == parentNode.rightChild) {
            node = parentNode;
            parentNode = parentNode.parent;
        }
        if (node.rightChild == null && node.leftChild != null)
        {
            return node.leftChild;
        }
        return parentNode;
    }
    /** * minElemNode: 获取二叉查找树中的最小关键字结点 * * @return 二叉查找树的最小关键字结点 * @throws Exception * 若树为空，则抛出异常 */
    public TreeNode minElemNode(TreeNode node) throws Exception {
        if (node == null) {
            throw new Exception("树为空！");
        }
        TreeNode pNode = node;
        while (pNode.leftChild != null) {
            pNode = pNode.leftChild;
        }
        return pNode;
    }

    /** * maxElemNode: 获取二叉查找树中的最大关键字结点 * * @return 二叉查找树的最大关键字结点 * @throws Exception * 若树为空，则抛出异常 */
    public TreeNode maxElemNode(TreeNode node) throws Exception {
        if (node == null) {
            throw new Exception("树为空！");
        }
        TreeNode pNode = node;
        while (pNode.rightChild != null) {
            pNode = pNode.rightChild;
        }
        return pNode;
    }


    public boolean isEmpty() {
        if (root == null) {
            return true;
        } else {
            return false;
        }
    }

    /** * precessor: 获取给定结点在中序遍历顺序下的前趋结点 * * @param node * 给定树中的结点 * @return 若该结点存在中序遍历顺序下的前趋结点，则返回其前趋结点；否则返回 null * @throws Exception */
    public TreeNode precessor(TreeNode node) throws Exception {
        if (node == null) {
            return null;
        }

        // 若该结点的左子树不为空，则其前趋结点就是左子树中的最大关键字结点
        if (node.leftChild != null) {
            return maxElemNode(node.leftChild);
        }
        // 若该结点左子树为空
        TreeNode parentNode = node.parent;
        while (parentNode != null && node == parentNode.leftChild) {
            node = parentNode;
            parentNode = parentNode.parent;
        }
        return parentNode;
    }

    /** * inOrderTraverse: 对给定二叉查找树进行中序遍历 * * @param root * 给定二叉查找树的根结点 */
    private void inOrderTraverse(TreeNode root) {
        if (root != null) {
            nodelist.add(root);
            inOrderTraverse(root.leftChild);
            inOrderTraverse(root.rightChild);

        }
    }

    public TreeNode getRoot() {
        return root;
    }




    public static void main(String[] args) {
        BinarySearchTree bst = new BinarySearchTree();
        System.out.println("查找树是否为空？ " + (bst.isEmpty() ? "是" : "否"));
        int[] keys = new int[] { 15, 6, 18, 3, 7, 13, 20, 2, 9, 4 };
        for (int key : keys) {
            bst.insert(key);
        }
        System.out.println("查找树是否为空？ " + (bst.isEmpty() ? "是" : "否"));
        bst.inOrderTraverse(bst.getRoot());
        System.out.println(bst.getRoot().getKey());
        if(bst.nodelist != null)
        {
            for (TreeNode value : bst.nodelist)
            {
                System.out.println(value.getKey());
            }
        }

    }
}