BZOJ 2002 弹飞绵羊 Link-Cut-Tree(LCT)

题目大意：

某天，Lostmonkey发明了一种超级弹力装置，为了在他的绵羊朋友面前显摆，他邀请小绵羊一起玩个游戏。游戏一开始，Lostmonkey在地上沿着一条直线摆上n个装置，每个装置设定初始弹力系数ki，当绵羊达到第i个装置时，它会往后弹ki步，达到第i+ki个装置，若不存在第i+ki个装置，则绵羊被弹飞。绵羊想知道当它从第i个装置起步时，被弹几次后会被弹飞。为了使得游戏更有趣，Lostmonkey可以修改某个弹力装置的弹力系数，任何时候弹力系数均为正整数。

LCT模板题。

首先这个序列从右往左捋一下肯定是一棵树。错了不对，是一颗森林。

而第二个操作可以随时改变这棵森林的结构

于是这道题很明显是动态树结构中的Link-Cut-Tree。

关于LCT的概念网上有很多 这里只列出一个关键点

就是如何找到链顶的父节点

其实虽然这个算法的实现方式是对每一条重链(想不出名字来了，就沿用轻重链剖分的名字吧)维护一棵Splay，但实质上每一棵树内所有的Splay树都是连在一起的。

听不懂？没事，我说过的话我自己也听不懂

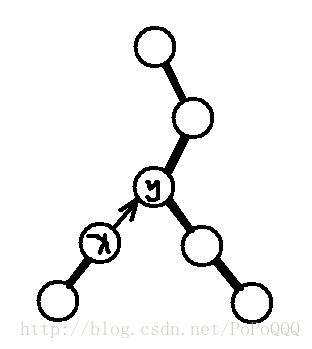
拿图来说话

其中加粗的边是重链

这里x所在重链和y所在重链存在的Splay树是相连的，x的父节点指向y，而y的子节点并不指向x

即x->fa=y,y->ls=null(或者其它节点)

这样就区分了这两条重链，也保证在Splay的时候由于x->fa->ls!=x，就不会影响到y所在的Splay树，同时也使x所在重链的任意节点Splay后，fa必然指向y

。。。再也不翘语文课了

总之贴代码 实在不懂可以拿这道题的代码调试一下 十分简单明了

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 200100
using namespace std;
int n,m;
struct abcd{
	abcd *ls,*rs,*fa;
	int siz;
	inline void Maintain() {  siz=ls->siz+rs->siz+1;  }
	abcd();
};
abcd *null=new abcd,tree[M];
abcd :: abcd()
{
	ls=rs=fa=null;
	siz=1;
}
void Zig(abcd*x)
{
	abcd*y=x->fa;
	abcd*z=y->fa;
	y->ls=x->rs;
	x->rs->fa=y;
	x->rs=y;
	y->fa=x;
	y->Maintain();
	x->Maintain();
	if (z->ls==y)
		z->ls=x;
	else if(z->rs==y)
		z->rs=x;
	x->fa=z;
}
void Zag(abcd*x)
{
	abcd*y=x->fa;
	abcd*z=y->fa;
	y->rs=x->ls;
	x->ls->fa=y;
	x->ls=y;
	y->fa=x;
	y->Maintain();
	x->Maintain();
	if (z->ls==y)
		z->ls=x;
	else if(z->rs==y)
		z->rs=x;
	x->fa=z;
}
void Splay(abcd*x)
{
	abcd *y,*z;
	for (;x->fa->ls==x||x->fa->rs==x;)
	{
		y=x->fa,z=y->fa;
		if (y->ls==x)
		{
			if (z->ls==y)
				Zig(y);
			Zig(x);
		}
		else
		{
			if (z->rs==y)
				Zag(y);
			Zag(x);
		}
	}
}
void Access(abcd *x)
{
	abcd *y=null;
	while(x!=null)
	{
		Splay(x);
		x->rs=y;
		x->Maintain();
		y=x;
		x=x->fa;
	}
}
void Link(abcd *x,abcd *y)
{
	Access(x);
	Splay(x);
	x->ls->fa=null;
	x->ls=null;
	x->fa=y;
	x->Maintain();
}
int main()
{
	null->ls=null->rs=null->fa=null;
	null->siz=0;
	int i,p,x,y;
	abcd *root;
	cin>>n;
	for (i=1;i<=n;i++)
	{
		scanf("%d",&x);
		if(i+x<=n)
			tree[i].fa=&tree[i+x];
	}
	cin>>m;
	for (i=1;i<=m;i++)
	{
		scanf("%d",&p);
		if(p==1)
		{
			scanf("%d",&x);x++;
			Access(&tree[x]);
			Splay(&tree[x]);
			printf("%d\n",tree[x].siz);
		}
		else
		{
			scanf("%d%d",&x,&y);x++;
			if(x+y<=n)
				root=&tree[x+y];
			else
				root=null;
			Link(&tree[x],root);
		}
	}
}