POJ 2396 Budget（无源汇网络有上下界的可行流-Dinic）

Description
有一个n*m的方阵，里面的数字未知，但是我们知道如下约束条件：
每一行的数字的和
每一列的数字的和
某些格子有特殊的大小约束，用大于号，小于号和等于号表示
问：是否存在用正数填充这个方阵的方案，满足所有的约束，若有，输出之，否则输出IMPOSSIBLE
Input
第一行为一个整数T表示用例组数，每组用例第一行为两个整数n和m表示行列数，第二行n个整数表示每行数字的和，第三行m个整数表示每列数字的和，然后是一个整数cnt表示限制数，之后cnt行每行一个限制a b op d，当a，b均不为0时表示a行b列的数与d的关系(op取=,<,>），当a或b为0时表示b列或a行整列或整行均与d有op的关系
Output
对于每组用例，如果存在用正数填充这个方阵的方案则输出，否则输出IMPOSSIBLE,每组输出后跟一空行
Sample Input
2

2 3
8 10
5 6 7
4
0 2 > 2
2 1 = 3
2 3 > 2
2 3 < 5

2 2
4 5
6 7
1
1 1 > 10
Sample Output
2 3 3
3 3 4

IMPOSSIBLE

Solution
求无源汇的网络有上下界的可行流
由于下界是一条弧上的流必需要满足的确定值。下面引入必要弧的概念：必要弧是一定要流满的弧。必要弧的构造，将容量下界的限制分离开了，从而构造了一个没有下界的网络G’：

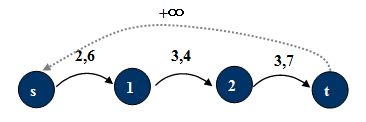
1． 将原弧(u,v)分离出一条必要弧：（红色表示）
2． 原弧：
由于必要弧的有一定要满的限制，将必要弧“拉”出来集中考虑：

添加附加源x, 附加汇y。想像一条不限上界的(y, x)，用必要弧将它们“串”起来，即对于有向必要弧(u, v)，添加(u, y)，(x, v)，容量为必要弧容量。这样就建立了一个等价的网络。

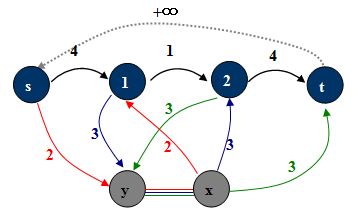
一个无源汇网络的可行流的方案一定是必要弧是满的。若去掉(y, x)后，附加源x到附加汇y的最大流，能使得x的出弧或者y的入弧都满，充要于原图有可行流。

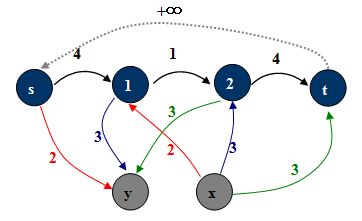
算法：
1. 按上述方法构造新网络(分离必要弧，附加源汇)
2. 求附加源x到附加汇y的最大流
3. 若x的出弧或y的入弧都满，则有解，将必要弧合并回原图；否则，无解
该题将每一行和每一列都看作一个点，然后根据输入的约束条件建图，附加源点到每个点的容量为该点入流的所有边的下界和，每个点到附加汇点的容量为该点出流的所有边的下界和，而分别统计这两个值比较麻烦，所以此处记录入流与出流差值tre，若tre>0则从附加源点向此点建容量为tre的边，否则从此点向附加汇点建容量为-tre的边，具体过程见代码注释
Code

#include<iostream> 
#include<cstdio> 
#include<cstring> 
using namespace std;  
#define maxn 555 
#define maxm 55555 
#define INF 0x3f3f3f3f 
struct node
{  
    int u,v,f,next;  
}edge[maxm];  
int head[maxn],p,lev[maxn],cur[maxn],que[maxm];
int tre[maxn],up[maxn][50],low[maxn][50];  
void init(int n,int m)//初始化 
{  
    p=0;
    memset(head,-1,sizeof(head));
    memset(tre,0,sizeof(tre));  
    for(int i=0;i<=n;i++) 
        for(int j=0;j<=m;j++)  
        {
            up[i][j]=INF;
            low[i][j]=0; 
        }
}  
bool bfs(int s,int t)
{  
    int qin=0,qout=0,u,i,v;  
    memset(lev,0,sizeof(lev));  
    lev[s]=1;
    que[qin++]=s;  
    while(qout!=qin)
    {  
        u=que[qout++];  
        for(i=head[u];i!=-1;i=edge[i].next)
        {  
            if(edge[i].f>0&&lev[v=edge[i].v]==0)
            {  
                lev[v]=lev[u]+1;
                que[qin++]=v;  
                if(v==t) 
                    return 1;  
            }  
        }  
    }  
    return lev[t];  
}  
int dinic(int s,int t)//求最大流 
{  
    int qin,u,i,k,f;  
    int flow=0;  
    while(bfs(s,t))
    {  
        memcpy(cur,head,sizeof(head));  
        u=s,qin=0;  
        while(1)
        {  
            if(u==t)
            {  
                for(k=0,f=INF;k<qin;k++)  
                    if(edge[que[k]].f<f)  
                        f=edge[que[i=k]].f;  
                for(k=0;k<qin;k++)  
                {
                    edge[que[k]].f-=f;
                    edge[que[k]^1].f+=f;  
                }
                flow+=f;
                u=edge[que[qin=i]].u;  
            }  
            for(i=cur[u];cur[u]!=-1;i=cur[u]=edge[cur[u]].next)  
                if(edge[i].f>0&&lev[u]+1==lev[edge[i].v]) 
                    break;  
            if(cur[u]!=-1)  
            {
                que[qin++]=cur[u];
                u=edge[cur[u]].v;  
            }
            else
            {  
                if(qin==0) 
                    break;  
                lev[u]=-1,u=edge[que[--qin]].u;  
            }  
        }  
    }  
    return flow;  
}  
void add(int u,int v,int f)//建边 
{  
    edge[p].u=u;
    edge[p].v=v;
    edge[p].f=f;
    edge[p].next=head[u];
    head[u]=p++;  
    edge[p].u=v;
    edge[p].v=u;
    edge[p].f=0;
    edge[p].next=head[v];
    head[v]=p++;  
}  
bool built(int n,int m)
{  
    for(int i=1;i<=n;i++)  
        for(int j=1;j<=m;j++)  
        {
            if(low[i][j]>up[i][j])//存在上界小于下界的点则必然不存在可行流 
                return 0;  
            tre[i]-=low[i][j];//i点tre值减去边i->j的容量下界 
            tre[j+n]+=low[i][j];//j+n点tre值加上边i->j的容量下界 
            add(i,j+n,up[i][j]-low[i][j]);//i点到j点建容量为上下界差值的边 
        }
    return 1;  
}  
void limitflow(int s,int t,int n,int m)
{  
    int i,j,x,y;  
    x=t+1;//附加源点t+1 
    y=t+2;//附加汇点t+2 
    for(i=0;i<=t;i++)//每个点都向附加源汇点建边 
    //(包括源汇点,因为源汇点相当于容量上下界相同的点,将其与附加源汇点建边后就不用再分别向各行各列表示的点建边了)
    {  
        if(tre[i]>0)//tre值为正则表示应在附加源点和该点间建边 
            add(x,i,tre[i]);  
        else if(tre[i]<0)//tre值为负责表示应在该点与附加汇点间建边 
            add(i,y,-tre[i]);  
    }  
    add(t,s,INF);//汇点向源点建容量为无穷的边 
    dinic(x,y);//求出附加原点到附加汇点的最大流 
    for(i=head[x];i!=-1;i=edge[i].next)
        if(edge[i].f)//残余网络中仍然存在容量不为0的边说明附加源点的出流(附加汇点的入流)不满,不存在可行流 
        {  
            printf("IMPOSSIBLE\n\n"); 
            return ;  
        }  
    for(i=head[t];i!=-1;i=edge[i].next)  
        if(edge[i].v==s) 
            break;  
    if(i<0)//不存在到源点的边则不存在可行流 
    {  
        printf("IMPOSSIBLE\n\n"); 
        return;  
    }  
    for(i=1;i<=n;i++)//输出可行方案 
    {  
        for(j=1;j<m;j++)  
            printf("%d ",edge[((i-1)*m+j)*2-1].f+low[i][j]);  
        printf("%d\n",edge[i*m*2-1].f+low[i][j]);  
    }  
    printf("\n");  
}  
int main()
{  
    int T;
    scanf("%d",&T);  
    while(T--)
    {  
        int n,m,u;
        scanf("%d%d",&n,&m);  
        int s=0;//源点为0 
        int t=n+m+1;//汇点为n+m+1 
        int sum1=0;//累加所有行数字和 
        int sum2=0;//累加所有列数字和 
        init(n,m);//初始化 
        for(int i=1;i<=n;i++)//将每行看作一个点,编号从1~n 
        {
            scanf("%d",&u);
            tre[s]-=u;//源点tre值减去该行的数字和 
            tre[i]+=u;//此行所表示的点的tre值加上该行的数字和 
            sum1+=u;
        }
        for(int i=n+1;i<=n+m;i++)//将每列看作一个点,编号从n+1~n+m 
        {
            scanf("%d",&u);
            tre[i]-=u;//此列所表示的点的tre值减去该列的数字和 
            tre[t]+=u;//汇点tre值加上该列的数字和 
            sum2+=u;  
        }
        int cnt;
        scanf("%d",&cnt);  
        while(cnt--)
        {  
            int u,v,d;
            char c[5];
            scanf("%d%d%s%d",&u,&v,c,&d);  
            int l1=u,r1=u;
            int l2=v,r2=v;  
            if(u==0)//u=0表示该行均被此关系约束 
                l1=1,r1=n;  
            if(v==0)//v=0表示该列均被此关系约束 
                l2=1,r2=m;  
            for(int i=l1;i<=r1;i++)//更新每个点的上下界 
                for(int j=l2;j<=r2;j++)
                {  
                    if(c[0]=='=')
                        low[i][j]=max(d,low[i][j]),up[i][j]=min(d,up[i][j]);  
                    else if(c[0]=='>')
                        low[i][j]=max(d+1,low[i][j]);  
                    else if(c[0]=='<')
                        up[i][j]=min(d-1,up[i][j]);  
                }  
        }  
        if(sum1==sum2&&built(n,m)) 
            limitflow(s,t,n,m);  
        else printf("IMPOSSIBLE\n\n");//所有行数字和与所有列数字和不等或者存在上界小于下界的点则一定不存在可行流 
    }  
    return 0;  
}