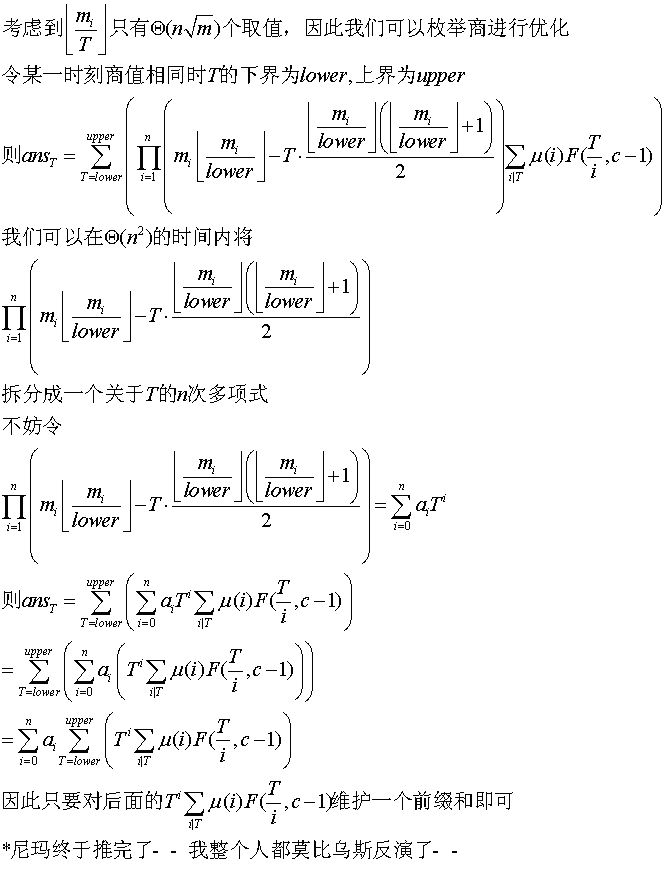
BZOJ 3434 Wc2014 时空穿梭 莫比乌斯反演

题目大意：给定一个n维空间，需要在这n维空间内选取c个共线的点，要求这c个点每维坐标均单调递增，第i维坐标是整数且在[1,mi]

为了表述方便令||代表中间东西的方案数 顺便设第i维坐标为ai 但是这样不简洁因此用x表示第1维坐标，y表示第二维坐标，θ表示第n维坐标

貌似我的方法SB了？不管了总之自己能推出来真是太好了- -

尼玛BZOJ渣评测机卡常数- - 明明UOJ5s就全过了的说- -

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define M 100100
#define MOD 10007
using namespace std;
int mu[M],prime[M],tot;
bool not_prime[M];
int f[M][20],mu_f[M][20],sum[M][20][12];
//f[i][j]表示和为i,长度为j的正整数排列的个数
//mu_f[T][j]表示c-1=j时Σ[i|T]mu[i]F[T/i]的值
//sum[T][j][k]表示c-1=j时T^k*Σ[i|T]mu[i]F[T/i]的前缀和
int n,c,min_m,m[12],a[12];
void Linear_Shaker()
{
	int i,j;
	mu[1]=1;
	for(i=2;i<=100000;i++)
	{
		if(!not_prime[i])
		{
			prime[++tot]=i;
			mu[i]=-1;
		}
		for(j=1;prime[j]*i<=100000;j++)
		{
			not_prime[prime[j]*i]=1;
			if(i%prime[j]==0)
			{
				mu[prime[j]*i]=0;
				break;
			}
			mu[prime[j]*i]=-mu[i];
		}
	}
}
void Pretreatment()
{
	int i,j,k;

	Linear_Shaker();

	for(i=1;i<=100000;i++)
	{
		f[i][1]=1;
		for(j=2;j<=i&&j<=19;j++)
			f[i][j]=(f[i-1][j]+f[i-1][j-1])%MOD;
	}

	for(i=1;i<=100000;i++)
		for(j=1;j<=19;j++)
			for(k=100000/i;k;k--)
				(mu_f[k*i][j]+=mu[i]*f[k][j])%=MOD;

	for(i=1;i<=100000;i++)
		for(j=1;j<=19;j++)
		{
			int temp=1;
			for(k=0;k<=11;k++,temp*=i,temp%=MOD)
				(sum[i][j][k]=sum[i-1][j][k]+mu_f[i][j]*temp%MOD)%=MOD;
		}
}
void Get_A(int lower)
{
	int i,j;
	memset(a,0,sizeof a);
	a[0]=1;
	for(i=1;i<=n;i++)
	{
		int d=m[i]/lower;
		int k=-((long long)d*(d+1)>>1)%MOD;
		int b=((long long)m[i]*d)%MOD;
		for(j=n;j;j--)
			(a[j]=k*a[j-1]+b*a[j])%=MOD;
		(a[0]*=b)%=MOD;
	}
}
int main()
{
	int T,i,j,last;
	Pretreatment();
	for(cin>>T;T;T--)
	{
		scanf("%d%d",&n,&c);
		min_m=0x3f3f3f3f;
		for(i=1;i<=n;i++)
		{
			scanf("%d",&m[i]);
			min_m=min(min_m,m[i]);
		}
		int ans=0;
		for(i=1;i<=min_m;i=last+1)
		{
			last=0x3f3f3f3f;
			for(j=1;j<=n;j++)
				last=min(last,m[j]/(m[j]/i) );
			Get_A(i);
			for(j=0;j<=n;j++)
				(ans+=a[j]*(sum[last][c-1][j]-sum[i-1][c-1][j])%MOD)%=MOD;
		}
		printf("%d\n",(ans+MOD)%MOD);
	}
	return 0;
}