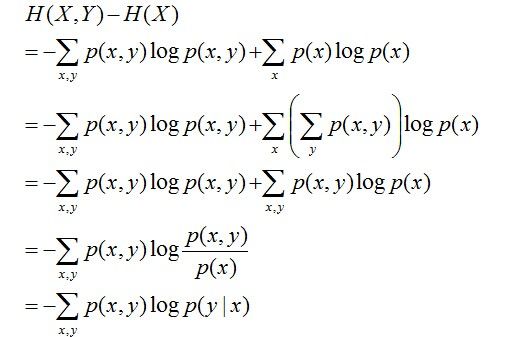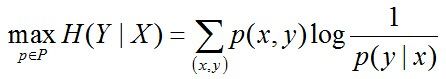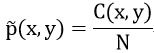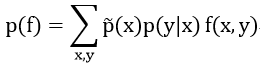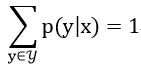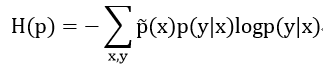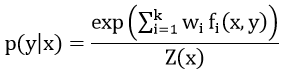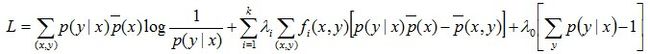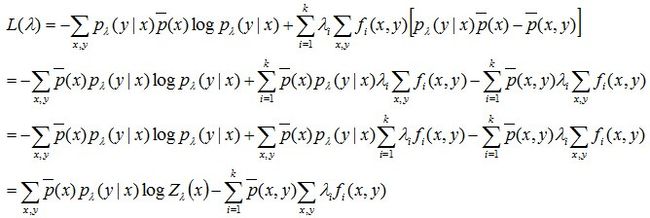基于最大熵模型的中文分词
字标注问题
先看一个句子：我是一名程序员。将所有字分为4类，S表示单字，B表示词首，M表示词中，E表示词尾。
如果我们知道上述句子中每个字的类别，即:
我/S 是/S 一/B 名/E 程/B 序/M 员/E 。/S
那么我们就可以知道这个句子的分词结果：我 是 一名 程序员 。
从这里可以看出，分词问题转化成了一个分类问题，即对每个字分类。
“熵”最初是热力学中的一个概念，上世纪40年代，香农首先在信息论中引入了信息熵的概念。信息熵用来表示不确定度的度量，不确定度越大，熵值越大。极限情况，当一个随机变量均匀分布时，熵值最大；完全确定时，熵值为0。如果没有外界干扰，随机变量总是趋向于无序，在经过足够时间的稳定演化，它应该能够达到的最大程度的熵。
最大熵模型的核心思想就是：为了估计随机变量的状态，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。这样也就等价于最大化熵，认为在所有可能的概率模型（分布）的集合中，熵最大的模型是最好的模型。
熵
熵公式如下
容易得到熵始终大于0的。
联合熵：两个随机变量X，Y的联合分布，可以形成联合熵Joint Entropy，用H(X,Y)表示。
条件熵：在随机变量X发生的前提下，随机变量Y发生所新带来的熵定义为Y的条件熵，用H(Y|X)表示，用来衡量在已知随机变量X的条件下随机变量Y的不确定性。
H(Y|X) = H(X,Y) – H(X)，整个式子表示(X,Y)发生所包含的熵减去X单独发生包含的熵。至于怎么得来的请看推导：
这个式子的实际含义就是加入x的标记后，相当于引入了一定的知识，那么就会减小y的不确定性，也就是减小了熵。
最大熵模型
最大熵模型的一般表达式
定义特征函数
x为上下文信息，而并非仅仅是目标词
y代表标签
特征考虑一个例子：记者王大勇，假设已经分过词，当前词为王大勇，前接词为记者。可以定义一条特征为：
下面两个期望要分清，这是算法的关键
定义特征函数f的经验期望如下：
示样本(x,y)在所有样本库中出现的概率，如果认为训练样本是真实情况的很好的近似，可以用训练语料D={(x_1 y_1 ),(x_2 y_2 )…(x_N y_N)}中出现的经验概率表示：
C(x,y)代表样本库中(x,y)出现的次数，N为样本库的样本数。
定义特征函数f的模型期望为：
同上，也用x在训练语料里出现的经验概率表示，也就是数数然后归一化。
最大熵模型的约束就是使得任意特征fi的经验期望和模型期望相等
根据概率公式的定义，我们还有另外一个约束：
所以我们就得到了一个有约束条件的最优化问题：
max：
subject to：
里面p(y|x)相当于自变量，我们需要得到的就是条件熵H(p)最大的模型p。
通过拉格朗日乘子法，求解
的极大值。
对p求偏导，并令偏导数等于0，得到取极值的条件
用λ和μ表示p，再利用消去μ，得到只含有λ的式子
则p用λ表示为
z(x)为归一化因子
z(x)=
化简得到只关于λ的式子
这样我们极大化L(λ)，求得λ的具体数值后模型也就确定了。这个问题的解法比较多，一般用GIS、IIS、LBFGS等方法。
import sys,math
def load_train_samples(fname):
'''
load training samples of (x,y) pairs
'''
fin = open(fname)
x = []; y = []
y_cate = {}
for sline in fin:
sline = sline.strip()
elem_lst = sline.split(' ')
x_i = []
for i in range(len(elem_lst)):
if i == 0:
y.append(elem_lst[i]) #first elem is class yi
y_cate[elem_lst[i]] = 1 #record y category
else:
x_i.append(elem_lst[i]) #follow elems are context xi
x.append(x_i)
fin.close()
return x, y, y_cate
class FeatureParam:
'''
definition of feature, feature function and its parameter
'''
def __init__(self, template_id, x_i, y_i):
self.w = 0.0 #initial parameter as 0
self.template_id = template_id #pre:=-1, cur:=0
self.cont_value = x_i[template_id+1]
self.cate_value = y_i
def feature_function(self, template_id, x_i, y_i):
if self.template_id == template_id and y_i == self.cate_value \
and x_i[template_id+1] == self.cont_value:
return 1
else:
return 0
#add feature when initializing
def add_features(features, feature_dict, template_id, x_i, y_i):
feat = FeatureParam(template_id, x_i, y_i)
feature_tuple = (feat.template_id, feat.cont_value, feat.cate_value)
if feature_tuple not in feature_dict:
features.append(feat)
feature_dict[feature_tuple] = 1
def init_feature_func_and_param(x,y):
'''
initial features from training samples
'''
features = []
feature_dict ={}
for i in range(len(x)):
x_i = x[i]
add_features(features, feature_dict, -1, x_i, y[i]) #feature of pre+label
add_features(features, feature_dict, 0, x_i, y[i]) #feature of cur+label
return features
def estimated_expect_feature_value(x, y, fparam):
'''
calculate the expect value of the feature in training samples
'''
esti_efi = 0.0
for i in range(len(x)):
x_i = x[i]
esti_efi += (fparam.feature_function(-1, x[i], y[i]) + fparam.feature_function(0, x[i], y[i]))
if esti_efi == 0.0:
esti_efi = 0.0000001
esti_efi /= 1.0*len(x) #time p(x,y)
return esti_efi
#calculate the common express of exp(SIGMA[para_i*feature_i])
def calculate_common_exp_value(x_i, y_i, features):
weight_sum = 0.0
for fparam in features:
weight_sum += fparam.w * (fparam.feature_function(-1, x_i, y_i) +\
fparam.feature_function(0, x_i, y_i))
return math.exp(weight_sum)
def model_expect_feature_value(x, y_cate, fparam, features, exp_record):
'''
calculate the expect value of the feature in model
'''
model_efi = 0.0
idx = 0
for x_i in x:
#print x_i
z = 0.0
efi = 0.0
for y_i in y_cate:
#print y_i,
if idx < len(exp_record):
exp_pf = exp_record[idx]
else:
exp_pf = calculate_common_exp_value(x_i, y_i, features)
exp_record.append(exp_pf)
z += exp_pf #normalizer
#print "z=%f"%z,
efi += exp_pf * (fparam.feature_function(-1, x_i, y_i) \
+ fparam.feature_function(0, x_i, y_i))
#print "efi=%f"%efi
idx += 1
efi /= z
model_efi += efi #SIGMA(p(y|x)*f(x,y))
model_efi /= len(x) #time p(x)
if model_efi == 0.0:
model_efi = 0.0000001
return model_efi
def update_param(x, y, y_cate, features, m):
'''
updata parameter in one iteration
'''
converged = True
exp_record = [] #record exp(SIGMA[para_i*feature_i]) value in each iteration
w_updated = [] #new parameter after updating
for fparam in features:
esti_efi = estimated_expect_feature_value(x, y, fparam)
model_efi = model_expect_feature_value(x, y_cate, fparam, features, exp_record)
delta_i = math.log(esti_efi/model_efi) / m
w_updated.append(fparam.w + delta_i)
'''
#Debug info display
'''
sys.stdout.write("feat(%d,%s,%s,%0.4f) esti_efi=%0.4f model_efi=%0.4f delta=%0.4f\n" % \
(fparam.template_id, fparam.cont_value, fparam.cate_value, \
fparam.w, esti_efi, model_efi, delta_i))
if abs(delta_i/(fparam.w+0.0000001)) >= 0.01: #check convergence
converged = False
for w in w_updated:
sys.stdout.write("%0.4f " % w)
print ''
for i in range(len(features)):
features[i].w = w_updated[i]
return converged
#calculate the normalizer of Z
def calculate_normalizer(x_i, y_cate, features):
z=0.0
for y_i in y_cate:
z += calculate_common_exp_value(x_i, y_i, features)
return z
def log_likelihood(x, y, features):
'''
calculate log likelihood value
'''
log_like = 0.0
for i in range(len(x)):
x_i = x[i]
y_i = y[i]
log_like += math.log(calculate_common_exp_value(x_i, y_i, features))
log_like -= math.log(calculate_normalizer(x_i, y, features))
log_like /= len(x)
return log_like
def max_ent_train(x, y, y_cate):
'''
training process by evaluating each parameters for every feature
'''
features = init_feature_func_and_param(x,y)
print "features_num=%d"%len(features)
m = 0.0
for i in range(len(x)):
for feat in features:
m += (feat.feature_function(-1, x[i], y[i])
+feat.feature_function(0, x[i], y[i]))
print "M=%0.2f"%m
iter_num = 0
while True:
print "============================= iteration_%d=============================="%iter_num
converged = update_param(x, y, y_cate, features, m)
log_like = log_likelihood(x, y, features)
print "log_likelihood=%0.12f"%log_like
if converged:
break
iter_num += 1
if iter_num > 10000:
break
print "finish training ..."
if __name__ == "__main__":
x,y,y_cate = load_train_samples("./test.txt")
max_ent_train(x, y, y_cate)