hdu 1542 Atlantis(线段树 面积并+扫描线)

http://acm.hdu.edu.cn/showproblem.php?pid=1542

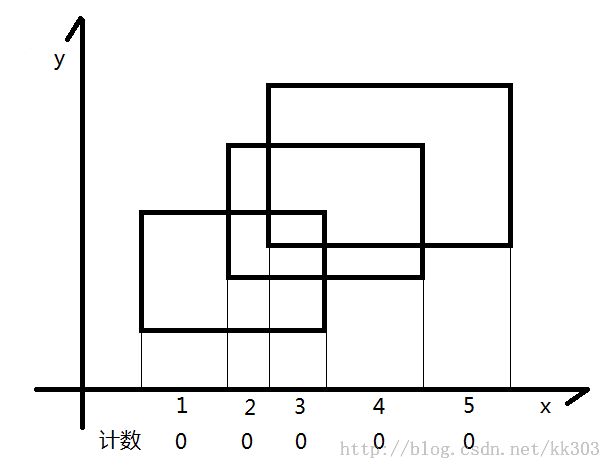
题意：给n个矩形的左下角和右上角的顶点坐标，求n个矩形的面积并。

思路：

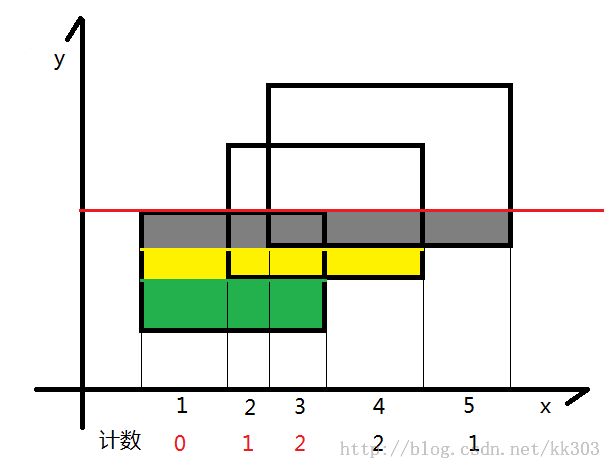
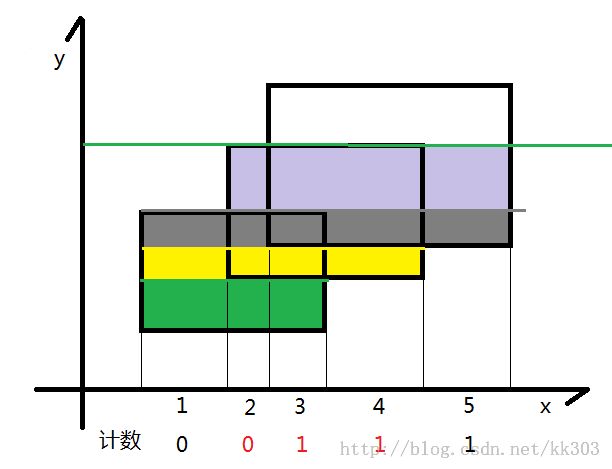
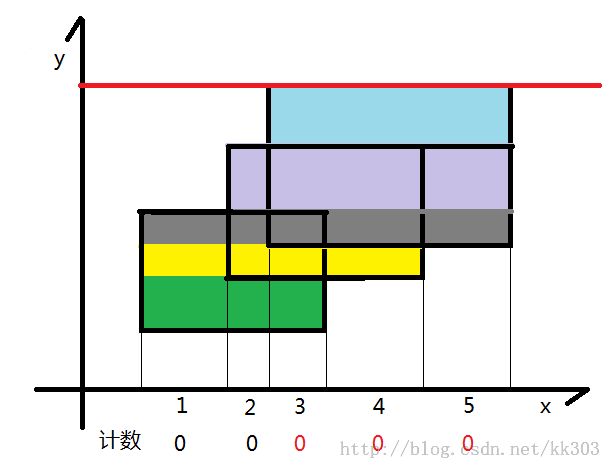
首先离散化，因为矩形端点坐标非常大。如果从下向上扫描，离散横坐标，如果从右向左扫描，离散纵坐标。这里，离散横坐标，从下向上扫描。

离散时，先对横坐标排序，去重，最后每个下标对应一个横坐标。

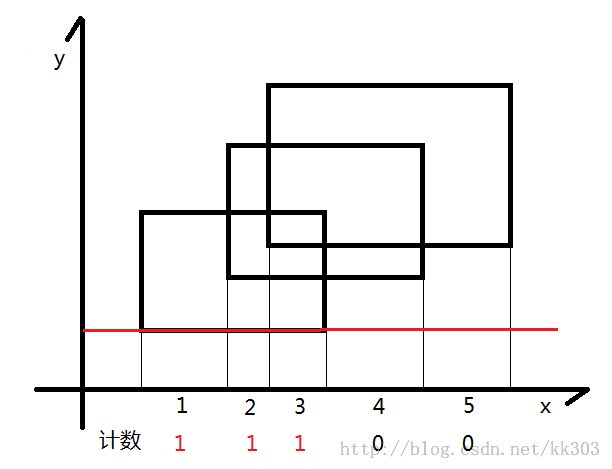
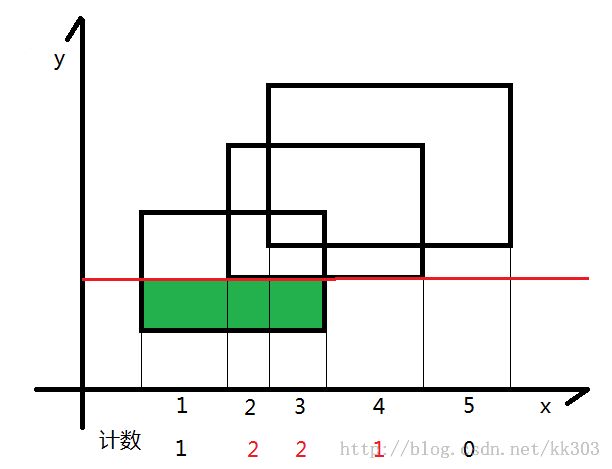
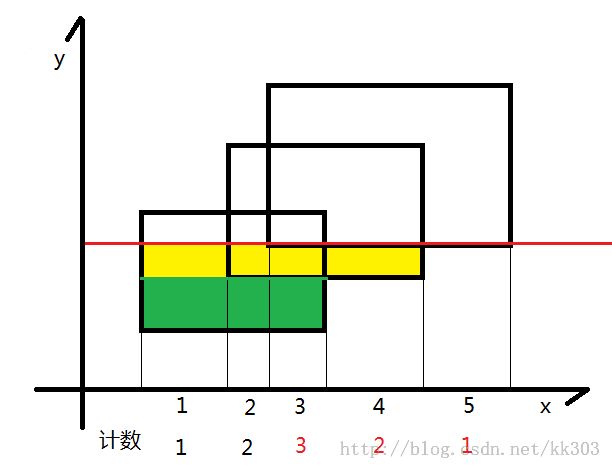
顺序扫描seg[]中的边，每扫描一条边，先找到该边对应离散后的左右端点（l,r）然后更新线段[l,r],如果该边是下边，那么对应的线段树区间+1，否则-1。若区间cnt > 0 ,说明该区间完全被覆盖，其长度可以直接算出。若区间cnt == 0,说明没有完全覆盖，由其左右儿子的区间覆盖长度和算出，区间cnt 不会出现负值，因为每次扫描都是从矩形的下边开始，扫描下边的时候cnt+1。每扫描一条边seg[i]，都要计算加上或删除这条边后（即更新后）总区间被覆盖的长度，用该长度乘seg[i+1].h-seg[i].h。最后累加。

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

const int maxn = 120;

struct node
{
    double l,r,h;
    int f;
    bool operator < (const struct node & tmp) const
    {
        return h < tmp.h;//按h从小到大排序
    }
}seg[maxn*2];

struct line
{
    int l,r;//线段左右端点
    int cnt;//该节点被覆盖的情况。正值完全覆盖，0不完全覆盖
    double len;//该节点被覆盖的长度
}tree[maxn*8];
double x[2*maxn];

void build(int v, int l, int r)
{
    tree[v].l = l;
    tree[v].r = r;
    tree[v].cnt = 0;
    tree[v].len = 0;
    if(l == r)
        return;
    int mid = (l+r)>>1;
    build(v*2,l,mid);
    build(v*2+1,mid+1,r);
}

int binsearch(double key,int k)//二分查找横坐标对应离散后的编号
{
    int low = 1;
    int high = k;
    while(low <= high)
    {
        int mid = (low+high)>>1;
        if(x[mid] == key)
            return mid;
        if(key < x[mid])
            high = mid-1;
        else low = mid+1;
    }
    return -1;
}

void getlen(int v)
{
    if(tree[v].cnt)//该节点完全覆盖，
    {
        tree[v].len = x[ tree[v].r+1 ] - x[ tree[v].l ];
        return;
    }

    if(tree[v].l == tree[v].r)//不是一条线段
    {
        tree[v].len = 0;
        return;
    }

    tree[v].len = tree[v*2].len + tree[v*2+1].len;
}

void update(int v, int l, int r, int f)
{
    if(tree[v].l == l && tree[v].r == r)
    {
        tree[v].cnt += f;
        getlen(v);
        return;
    }
    int mid = (tree[v].l + tree[v].r)>>1;
    if(r <= mid)
        update(v*2,l,r,f);
    else if(l > mid)
        update(v*2+1,l,r,f);
    else
    {
        update(v*2,l,mid,f);
        update(v*2+1,mid+1,r,f);
    }
    getlen(v);
}

int main()
{
    int n;
    double a,b,c,d;
    int item = 1;
    while(~scanf("%d",&n)&&n)
    {
        int num = 1;
        for(int i = 1; i <= n; i++)
        {
            scanf("%lf %lf %lf %lf",&a,&b,&c,&d);
            seg[num].l = a;
            seg[num].r = c;
            seg[num].h = b;
            seg[num].f = 1;
            x[num++] = a;

            seg[num].l = a;
            seg[num].r = c;
            seg[num].h = d;
            seg[num].f = -1;
            x[num++] = c;
        }

        sort(seg+1,seg+num);
        sort(x+1,x+num);

        int k = 1;
        for(int i = 2; i < num; i++)
        {
            if(x[i] != x[i-1])		//去重
                x[++k] = x[i];
        }
	
        build(1,1,k);
        double ans = 0;
        for(int i = 1; i < num; i++)
        {
            int l = binsearch(seg[i].l,k);
            int r = binsearch(seg[i].r,k)-1;

            update(1,l,r,seg[i].f);
            ans += (seg[i+1].h - seg[i].h)*tree[1].len;
        }
        printf("Test case #%d\n",item++);
        printf("Total explored area: %.2lf\n\n",ans);
    }
    return 0;
}

以下是转载：

 扫描线..可以看成一根平行于x轴的直线..至y=0开始往上扫..直到扫出最后一条平行于x轴的边..但是真正在做的时候..不需要完全模拟这个过程..扫描线的做法是从最下面的边开始扫到最上面的边.

   线段树: 本题用于动态维护扫描线在往上走时..x哪些区域是有合法面积的..

   几个图说明扫描线扫描..线段树维护的过程..:

初始状态

扫到最下边的线,点更新1~3为1

扫到第二根线,此时将计数器不为0的长度*上线两根线的长度,得到绿色的面积,加到答案中去.随后更新计数

同上,将黄色的面积加到答案中去

同上,将灰色的面积加到答案中去

同上,将紫色的面积加到答案中去

同上,将蓝色的面积加到答案中去