【计算几何壮丽而荡漾】稍微谈谈凸包。

（本文部分转载）原文地址：http://blog.csdn.net/hqd_acm/article/details/6218420

凸包(Convex Hull)：给一堆点， 框起来的凸起来的多边形的最大的连线，就叫凸包（个人理解定义）

问题
给定平面上的二维点集，求解其凸包。

过程：

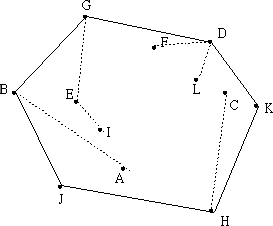
1. 在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。（最卡(0.0)的点)...坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据向量的内积公式求出向量的模即可。以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上，接着加入C。假设线段<K, C>也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K, D>才会在凸包上，所以将线段<K, C>排除，C点不可能是凸包。

3. 即当加入一点时，必须考虑到前面的线段是否会出现在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为p_{n + 1}，上一点为p_n，再上一点为p_{n - 1}。顺时针扫描时，如果向量<p_{n - 1}, p_n>与<p_n, p_{n + 1}>的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

在上图中，加入K点时，由于线段<H,K>相对于<H,C>为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K, D>相对<H, K>为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍例完成，即得到凸包。

模板代码，在网上代码的基础上。经过了本人的规范化，值得收藏。

#include<iostream>
　　#include<algorithm>
　　using namespace std;
　　struct point
　　{
　　int x;
　　int y;
　　}p[30005],res[30005]; //p标记图中所有的点，res标记凸包上的点
　　int cmp(point p1,point p2)
　　{
　　return p1.y<p2.y||(p1.y==p2.y&&p1.x<p2.x);
　　}
　　bool ral(point p1,point p2,point p3) //用叉乘判断点的位置
　　{
　　if((p2.x-p1.x)*(p3.y-p1.y)>(p3.x-p1.x)*(p2.y-p1.y)) return true;
　　return false;
　　}
　　int main()
　　{
　　int n,i,j;
　　while(scanf("%d",&n)!=EOF) //一共有n个点
　　{
　　for(i=0;i<n;i++)
　　scanf("%d%d",&p[i].x,&p[i].y);
　　if(n==1)
　　{
　　printf("%d %d",&p[0].x,&p[0].y);
　　continue;
　　}
　　if(n==2)
　　{
　　printf("%d %d\n",&p[0].x,&p[0].y);
　　printf("%d %d\n",&p[1].x,&p[1].y);
　　continue;
　　}
　　sort(p,p+n,cmp);
　　res[0]=p[0];
　　res[1]=p[1];
　　int top=1;
　　for(i=2;i<n;i++)
　　{
　　while(top&&!ral(res[top],res[top-1],p[i]))
　　top--;
　　res[++top]=p[i];
　　}
　　int len=top;
　　res[++top]=p[n-2];
　　for(i=n-3;i>=0;i--)
　　{
　　while(top!=len&&!ral(res[top],res[top-1],p[i]))
　　top--;
　　res[++top]=p[i];
　　}
　　for(i=0;i<top;i++)
　　printf("%d %d\n",res[i].x,res[i].y); //输出凸包上的点
　　}
　　}