二分图匹配

二分图：设G=(V,{R})是一个无向图。如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。

匹配：给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

最大匹配：匹配中边数最多的匹配。

完全匹配（完备匹配）：如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

最小覆盖：最小覆盖要求用最少的点（X集合或Y集合的都行）让每条边都至少和其中一个点关联。结论：最小覆盖 = 最大匹配。

最小路径覆盖：给出一个有向图G=（V，E），设 P 是 G 的一个简单路径的集合，若 G 中每个顶点都在 P 中的路径上，则称 P 为图 G 的一个路径覆盖。G 的最小路径覆盖是 G 的所有路径覆盖中所含路径条数最小的覆盖。把所有节点 u 拆分为两个：X 结点 ux 和 Y 结点 uy，如果 G 中存在有向边 u->v，则在二分图中引 ux->uy ，若最大匹配数为 m ，结点数位 n ，则最小路径覆盖数位 n-m 。   

最大独立集：在N个点的图G中选出m个点，使这M个点两两之间没有边，求m最大值。如果图G满足二分图条件，则可以用二分图匹配来做：最大独立集数 = N - 最大匹配数。

带权图的最佳匹配：给出一个带权二分图，求权值最大的匹配。KM 算法。

算法：二分图的最大匹配有 2 种实现，网络流和匈牙利算法。

     匈牙利算法是求解最大匹配的有效算法，该算法用到了增广路的定义(也称增广轨或交错轨)：若边集合P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

由增广路径的定义可以推出下述三个结论：

    1. P的路径长度必定为奇数，第一条边和最后一条边都不属于M。

       2.  P经过“取反操作”（即非M中的边变为M中的边，原来M中的边去掉）可以得到一个更大的匹配M’。

       3.  M为G的最大匹配当且仅当不存在相对于M的增广路径。

从而可以得到求解最大匹配的匈牙利算法：

        (1)置M为空

        (2)找出一条增广路径P，通过“取反操作”获得更大的匹配M’代替M

        (3)重复(2)操作直到找不出增广路径为止

根据该算法，可以选择深搜或者广搜实现，下面给出易于实现的深度优先搜索（DFS）实现。

匈牙利算法：

模板如下：

#include <cstdio>
#include <cstring>
#define MAXN 102

int n, m, match;
bool map[MAXN][MAXN];
int mat[MAXN];
bool used[MAXN];

bool CrossPath(int k) {
    for (int j=1; j<=m; j++) {
        if (!used[j] && map[k][j]) {
            used[j]=true;
            if (mat[j]==0 || CrossPath(mat[j])) {
                mat[j]=k;
                return true;
            }
        }
    }
    return false;
}

void hungary() {
    memset(mat, 0, sizeof(mat));
    for (int i=1; i<=n; i++) {
        memset(used, false, sizeof(used));
        if (CrossPath(i))
            match++;
    }
}

int main() {
    int a, b, nEdges;
    scanf("%d %d", &n, &m);   //set A: n个元素；set B: m个元素
    scanf("%d", &nEdges);
    while (nEdges--) {
        scanf("%d %d", &a, &b);
        map[a][b] = true;
    }
    match = 0;
    hungary();
    printf("%d\n", match);
    return 0;
}

以下转载自：http://hi.baidu.com/__%D2%E5__/blog/item/e9a05dc34c98f63de4dd3b90.html

带权二分图的最优匹配 Kuhn-Munkres算法

    分工问题如下：某公司有工作人员x1,x2,...,xn,他们去做工作y1,y2,...,yn,每人适合做其中的一项或几项工作，每个人做不同的工作的效益不一样，我们需要制定一个分工方案，使公司的总效益最大，这就是所谓最佳分配问题， 它们数学模型如下：

 数学模型：
    G是加权完全二分图，V(G)的二分图划分为X，Y；X={x1,...,xn},Y={y1,y2,...yn},w(xiyi)>=0是工作人员xi做yi工作时的效益，求权最大的完备匹配，这种完备匹配称为最佳匹配。
这个问题好象比较的棘手，用穷举法的话举也举死了，效率很低。本节给出一种有效算法，为此，先引入一个定义和一个定理。

定义1   映射 l : V(G)->R，满足：任意x∈X,任意y∈Y,成立
             l(x)+l(y) >= w(xy),
则称l(v)是二分图G的可行顶标；令
             El = {xy|xy∈E(G),l(x)+l(y)=w(xy)},
称以El为边集的G之生成子图为相等子图，记为Gl
可行顶标是存在的，例如
           l(x) = max w(xy),x∈X;
           l(y) = 0, y∈Y.

定理1 ：Gl的完备匹配即为G的最佳匹配。
证：设M*是Gl的一个完备匹配，因Gl是G的生成子图，故M*也是G的完备匹配。M*中的边之端点集合含G的每个顶点恰一次，所以
          W(M*)=Σw(e)=Σl(v) (e∈M*,v∈V(G)).
另一方面，若M是G中任意一个完备匹配，则
          W(M)=Σw(e)<=Σl(v) (e∈M,v∈V(G)),
所以
          W(M*)>=W(M)，
即M*是最佳匹配，证毕。

定理1告知，欲求二分图的最佳匹配，只需用匈牙利算法求取其相等子图的完备匹配；问题是，当Gl中无完备匹配时怎么办？Kuhn和Munkras给出修改顶标的一个算法，使新的相等子图的最大匹配逐渐扩大，最后出现相等子图的完备匹配。

Kuhn-Munkras算法：
        (0) 选定初始的可行顶标l,确定Gl,在Gl中选取一个匹配M。
        (1) X中顶皆被M许配，止，M即为最佳匹配；否则，取Gl中未被M许配的顶u,令S={u},T为空。
        (2) 若N(S)真包含T，转(3)；若N(S)=T，取
                 al=min(l(x)+l(y)-w(xy)}(x∈S,y∈T),
                 l(v)-al,v∈S;
                 l(v)= l(v)+al,v∈T;
                 l(v),其它。
                 l=l,Gl=Gl。
         (3) 选N(S)-T中一顶y,若y已被M许配，且yz∈M,则S=S∪{z},T=T∪{y},转(2)；否则，取Gl中一个M的可增广轨P(u,y),令M=M⊙E(P)，转(1)。

上面的算法看得有点莫名，改那个可行顶标怎么改改就好了？还是得看盾例子
例1   已知K5,5的权矩阵为
           y1 y2 y3 y4 y5
     x1   3  5   5   4   1
     x2   2  2   0   2   2
     x3   2  4   4   1   0
     x4   0  1   1   0   0
     x5   1  2   1   3   3

求最佳匹配，其中K5,5的顶划分为X={xi},Y={yi},i=1,2,3,4,5.
解：(1)取可行顶标l(v)为

l(yi)=0,i=1,2,3,4,5；

l(x1)=max(3,5,5,4,1}=5,l(x2)=max{2,2,0,2,2}=2,l(x3)=max(2,4,4,1,0}=4,l(x4)=max{0,1,1,0,0}=1,l(x5)=max{1,2,1,3,3}=3.
(2) Gl及其上之匹配见图7.12。
这个图中ο(G-x2)=3,由Tutte定理知无完备匹配。需要修改顶标。(3) u=x4,得S={x4,x3,x1},T={y3,y2},N(S)=T,于是
       al=min(l(x)+l(y)-w(xy)}=1. (x∈S,y∈T)
       x1,x2,x3,x4,x5的顶标分别修改成4,2,3,0,3；y1,y2,y3,y4,y5的顶标分别修改成0,1,1,0,0。
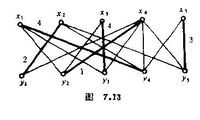
(4) 用修改后的顶标l得Gl及其上面的一个完备匹配如图7.13。图中粗实线给出了一个最佳匹配，其最大权是2+4+1+4+3=14。

我们看出：al>0；修改后的顶标仍是可行顶标；Gl中仍含Gl中的匹配M；Gl中至少会出现不属于M的一条边，所以会造成M的逐渐增广。 得到可行顶标后求最大匹配：

书上这部分没讲，实际上是这样的，对于上面这个例子来说，通过Kuhn-Munkres得到了顶标l(x)={4,2,3,0,3},l(y)={0,1,1,0,0},那么，对于所有的l(xi)+l(yj) = w(i,j)，在二分图G设置存在边w(i,j)。再用匈牙利算法求出最大匹配，再把匹配中的每一边的权值加起来就是最后的结果了。

KM算法模板：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define MAXN 305
#define INF 99999999

int w[MAXN][MAXN];
int lx[MAXN], ly[MAXN];
bool sx[MAXN], sy[MAXN];
int pre[MAXN], slack;
int n, m;

bool CrossPath(int u) {
    sx[u] = true;
    for(int i = 0; i < m; i++) {
        if(sy[i]) continue;
        int tmp = lx[u] + ly[i] - w[u][i];
        if(!tmp) {
            sy[i] = true;
            if(pre[i] == -1 || CrossPath(pre[i])) {
                pre[i] = u;
                return true;
            }
        } else if(slack > tmp) slack = tmp;
    }
    return false;
}

int KM() {
    int i, j, k, res;
    memset(pre, -1, sizeof(pre));
    memset(ly, 0, sizeof(ly));
    for(i = 0; i < n; i++)
        for(lx[i]=-INF, j = 0; j < m; j++)
            lx[i] = max(lx[i], w[i][j]);
    for(k = 0; k < n; k++) {
        while(1) {
            slack = INF;
            memset(sx, false, sizeof(sx));
            memset(sy, false, sizeof(sy));
            if(CrossPath(k)) break;
            for(i = 0; i < n; i++)
                if(sx[i]) lx[i] -= slack;
            for(i = 0; i < m; i++)
                if(sy[i]) ly[i] += slack;
        }
    }
    res = 0;
    for(i = 0; i < m; i++)
        res += w[pre[i]][i];
    return res;
}

int main() {
    int i, j, ans;
    while(scanf("%d", &n) != EOF) {
        m = n;
        for(i = 0; i < n; i++)
            for(j = 0; j < m; j++)
                scanf("%d", &w[i][j]);
        ans = KM();
        printf("%d\n", ans);
    }
    return 0;
}