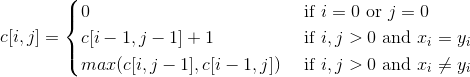《算法导论》笔记 第15章 15.4 最长公共子序列

【笔记】

【练习】

15.4-1 确定<1,0,0,1,0,1,0,1>和<0,1,0,1,1,0,1,1,0>的一个LCS。

1 0 0 1 1 0

15.4-2 说明如何通过表c和原始序列X=<x1,x2,...,xm>与Y=<y1,y1,...,yn>，在O(m+n)时间内重构一个LCS。

void printLcs2(int c[maxn][maxn], char x[], char y[],int i,int j) {
    if (i == 0 || j == 0) return;
    if (x[i] == y[j]) {
        printLcs2(c,x,y,i-1,j-1);
        cout<<x[i]<<" ";
    }
    else if (c[i-1][j]>=c[i][j-1]) { printLcs2(c,x,y,i-1,j); }
    else { printLcs2(c,x,y,i,j-1); }
}

15.4-3 请给出一个LCS-LENGTH的运行时间为O(mn)的备忘录版本。

int lcsLength2(char sx[], char sy[], int c[maxn][maxn], int b[maxn][maxn], int i,int j) {
    if (c[i][j] != -1) return c[i][j];
    if (sx[i] == sy[j]) {
        c[i][j] = lcsLength2(sx,sy,c,b,i-1,j-1) + 1;
        b[i][j] = LEFTUP;
    }
    else {
        int l=lcsLength2(sx,sy,c,b,i-1,j);
        int r=lcsLength2(sx,sy,c,b,i,j-1);
        if ( l >= r ) {
            c[i][j] = l;
            b[i][j] = UP;
        }
        else {
            c[i][j] = r;
            b[i][j] = LEFT;
        }
    }
    return c[i][j];
}

15.4-4 说明如何仅用表c中的2·min(m,n)项以及O(1)的额外空间来计算一个LCS的长度。然后说明如何用min(m,n)项以及O(1)的额外空间来做到这一点。

15.4-5 请给出一个O(n^2)时间的算法，使之能找出一个n个数的序列中最长的单调递增子序列。

*15.4-6 请给出一个O(nlgn)时间的算法，使之能找出一个n个数的序列中最长的单调递增子序列。

void LIS(int a[],int f[],int n) {
    vector<int>d;
    int r;
    for (int i=0;i<n;i++) {
        r=lower_bound(d.begin(),d.end(),a[i])-d.begin();
        if (r == d.size()) d.push_back(a[i]);
        else d[r]=a[i];
        f[i]=r+1;
    }
}