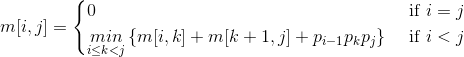《算法导论》笔记 第15章 15.2 矩阵链乘法

【笔记】

给定n个矩阵构成的一个链<A1,A2,...,An>，其中i=1,2,...,n，矩阵Ai的维数为p(i-1)*p(i)，对乘积A1A2...An以一种最小化标量乘法次数的方式加括号。

计算全部括号的重数：

递归解：

【练习】

15.2-1 对维数为序列<5,10,3,12,5,50,6>的各矩阵，找出其矩阵链乘积的一个最优加全部括号。

15.2-2 请给出一个递归算法MATRIX-CHAIN-MULTIPLY(A,s,i,j)，使之在给出矩阵序列<A1,A2,...,An>，和由MATRIX-CHAIN-ORDER计算出的表s，以及下标i和j后，能得出一个最优的矩阵链乘法。

15.2-3 使用替换法证明递归公式的解为Ω(2^n)。

15.2-4 设R(i,j)表示在调用MATRIX-CHAIN-ORDER中计算其他表项时，表项m[i,j]被引用的次数。证明：对整个表总的引用次数为

15.2-5 证明：一个含n个元素的表达式的加全部括号中恰有n-1对括号。