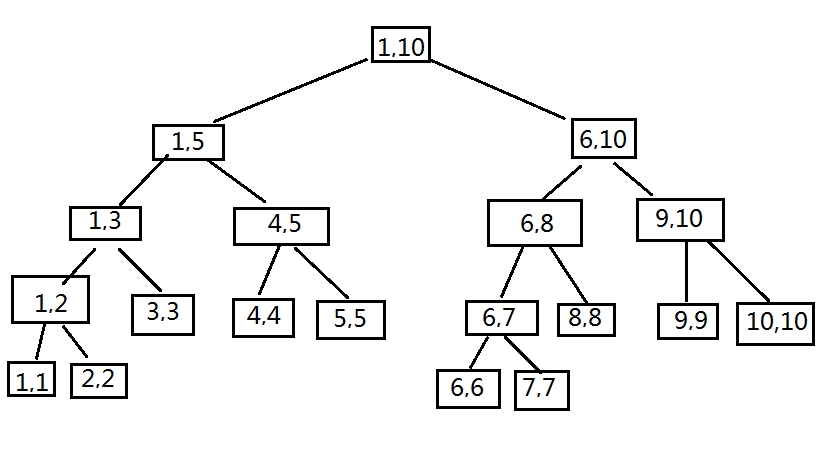
线段树

谈对线段树的理解：

线段树又称（区间树），实质就是：树中节点可表示一个区间，所以称为区间树更合适一些。节点中可添加适当的数据来实现相应的一些操作，每个节点的数据都是建立在左子树和右子树之上。这样做的目的使查找效率从O(n)降为O(log(n))

线段树的模型：

适用与使用线段树解决的问题：某些数据需要按区间进行区分，按区间进行修改，而且需要多次按区间进行查询。例如多次查询第k小元素，多次查询区间内最大最小元素。

推荐题型：

hdoj4217，第一次接触线段树

#include <cstdio>
const int nMax=262144;
struct Node
{
	int l,r;
	int len;
	Node(int l,int r,int len):l(l),r(r),len(len){}
	Node(){}
}node[nMax<<2];//①，这里需要注意一下
int ans;
void build(int l,int r,int rt)
{
	node[rt]=Node(l,r,r-l+1);
	if(l<r)
	{
		int mid=(l+r)>>1;
		build(l,mid,rt<<1);
		build(mid+1,r,rt<<1 | 1);
	}
}
void update(int p,int rt)
{
	if(p > node[rt].len)
	{
		ans = -1;
		return ;
	}
	-- node[rt].len;
	if(node[rt].l == node[rt].r)
	{
		ans = node[rt].l;
		return ;
	}
	else
	{
		if(p <= node[rt << 1].len)
		{
			update(p, rt << 1);
		}
		else
		{
			update(p - node[rt << 1].len,rt << 1 | 1);
		}
	}
}
int main()
{
	freopen("f://data.in","r",stdin);
	int T;
	int n,k,ki;
	scanf("%d",&T);
	for(int cas=1;cas<=T;cas++)
	{
		__int64 sum=0;//②
		scanf("%d %d",&n,&k);
		build(1,n,1);
		for(int i=0;i<k;i++)
		{
			scanf("%d",&ki);
			update(ki,1);
			sum+=ans;
		}
		printf("Case %d: %I64d\n",cas,sum);
	}
	return 0;
}

poj3264，基础题型

/*
题意：N头母牛已排序好，分别输入它们的身高，Q组测试数据，每组测试数据（a,b)输出从第a到b母牛的最高身高和最低身高之差。

AC,一般难度，主要在线段树中数据结构的建立。
新题要尝试自己去解决，不是你不会，而是你不敢去尝试。重在思路。


*/
#include <cstdio>
const int nMax=50010;
int N,Q;
struct Tree
{
	int l,r,min,max;
	Tree(){}
	Tree(int l,int r,int min,int max):l(l),r(r),min(min),max(max){}
}tree[nMax<<2];
int Ni[nMax];
void build(int l,int r,int rt,int &min,int &max)
	//因为自定义数据结构中有了min和max，所以如果不传递min和max也可以实现。根据tree构建时的规律。
{
	if(l==r)
	{
		tree[rt]=Tree(l,l,Ni[l],Ni[l]);
		min=max=Ni[l];
	}
	else
	{
		int min1,max1,min2,max2;
		int mid=(l+r)>>1;
		build(l,mid,rt<<1,min1,max1);
		build(mid+1,r,rt<<1 | 1,min2,max2);
		min=min1<min2?min1:min2;
		max=max1>max2?max1:max2;
		tree[rt]=Tree(l,r,min,max);
	}
}
void search(int l,int r,int rt,int &min,int &max)//①
{
	if(l==r)
	{
		min=max=Ni[l];
		return;
	}
	else if(tree[rt].l==l && tree[rt].r==r)
	{
		min=tree[rt].min;
		max=tree[rt].max;
		return;
	}
	int mid=(tree[rt].l+tree[rt].r)>>1;
	if(mid<l)
		search(l,r,rt<<1 | 1,min,max);
	else if(mid>=r)
		search(l,r,rt<<1,min,max);
	else
	{
		int min1,min2,max1,max2;
		search(l,mid,rt<<1,min1,max1);
		search(mid+1,r,rt<<1 | 1,min2,max2);
		min=min1<min2?min1:min2;
		max=max1>max2?max1:max2;
	}
}
int main()
{
	//freopen("f://data.in","r",stdin);
	scanf("%d %d",&N,&Q);
	for(int i=1;i<=N;i++)
	{
		scanf("%d",&Ni[i]);
	}
	int min0,max0;
	build(1,N,1,min0,max0);
	for(int i=1;i<=Q;i++)
	{
		int a,b;
		scanf("%d %d",&a,&b);
		int min,max;
		search(a,b,1,min,max);
		printf("%d\n",max-min);
	}
	return 0;
}

hdoj2795，加深理解，还不错

/*
题意：广告栏，高h、宽w，向广告栏里粘贴广告，每个广告高*宽为1*wi，n组数据，分别输入广告宽度wi。粘贴的规律：高度从低到高，依次粘贴，只到这一栏贴不下了，换下一栏。如果到最后都贴不下，输出-1，否则输出所在的栏的高度编号。

AC,WA了N多次，最后发现是①处的错误，There are multiple cases (no more than 40 cases).
其实线段树，问题的关键就是要建立自己的模型，找到最合适的数据结构
方法一：使用成员变量max来表示左子树和右子树最大值。
方法二：使用lmax变量来表示左子树最大值。
方法二是自己想的，但显然方法一比较好一些，方法二的实现也有一些问题。


做完这个题，感觉线段树掌握的差不多了。
*/
#include <cstdio>
const int nMax=200000;
struct Tree
{
	int l,r;
	int max;
	Tree(){max=0;}
	Tree(int l,int r,int max):l(l),r(r),max(max){}
}tree[nMax<<2];
int ans;
int h,w,n;
int fmax(int a,int b)
{
	return a>b?a:b;
}
void build(int l,int r,int rt)
{
	tree[rt]=Tree(l,r,w);
	if(l==r) return;
	int mid=(l+r)>>1;
	build(l,mid,rt<<1);
	build(mid+1,r,rt<<1 | 1);
}
void update(int p,int rt)
{
	if(tree[rt].max<p)
	{
		ans=-1;
		return;
	}
	if(tree[rt].l==tree[rt].r)
	{
		ans=tree[rt].l;
		tree[rt].max-=p;
		return;
	}
	if(tree[rt<<1].max>=p)
	{
		update(p,rt<<1);
		tree[rt].max=fmax(tree[rt<<1].max,tree[rt<<1 | 1].max);
	}
	else
	{
		update(p,rt<<1 | 1);
		tree[rt].max=fmax(tree[rt<<1].max,tree[rt<<1 | 1].max);
	}
}
int main()
{
	//freopen("f://data.in","r",stdin);
	while(scanf("%d %d %d",&h,&w,&n)!=EOF)//①
	{
		int N=h<n?h:n;
		build(1,N,1);
		for(int i=0;i<n;i++)
		{
			ans=-1;
			int wi;
			scanf("%d",&wi);
			update(wi,1);
			printf("%d\n",ans);
		}
	}
	return 0;
}

//方法二，WA
#include <cstdio>
const int nMax=200000;
struct Tree
{
	int l,r;
	int lmax;
	Tree(){lmax=0;}
	Tree(int l,int r,int lmax):l(l),r(r),lmax(lmax){}
}tree[nMax<<2];
int ans;
int h,w,n;
void build(int l,int r,int rt)
{
	tree[rt]=Tree(l,l,w);
	if(l==r) return;
	int mid=(l+r)>>1;
	build(l,mid,rt<<1);
	build(mid+1,r,rt<<1 | 1);
	tree[rt]=Tree(l,r,w);
}
void update(int p,int l,int r,int rt)
{
	if(l==r)
	{
		if(tree[rt].lmax>=p)
		{
			ans=l;
			tree[rt].lmax-=p;
		}
		return;
	}
	int mid=(l+r)>>1;
	if(p<=tree[rt].lmax)
	{
		update(p,l,mid,rt<<1);
		int lrt=rt<<1;
		int lrrt=lrt<<1 | 1;
		int max1=0,max2=0;
		if(lrt<(nMax<<2)) max1=tree[lrt].lmax;
		if(lrrt<(nMax<<2)) max2=tree[lrrt].lmax;
		tree[rt].lmax=max1>max2?max1:max2;
	}
	else
		update(p,mid+1,r,rt<<1 | 1);
}
int main()
{
	//freopen("f://data.in","r",stdin);
	while(scanf("%d %d %d",&h,&w,&n)!=EOF)
	{
		int N=h<n?h:n;
		build(1,N,1);
		for(int i=0;i<n;i++)
		{
			ans=-1;
			int wi;
			scanf("%d",&wi);
			update(wi,1,N,1);
			printf("%d\n",ans);
		}
	}
	return 0;
}

poj2182，推荐题型。。。

/*
题意：N头母牛，他们都有自己唯一的编号（从1到N），然后输入N-1组数据，每组数据Ni[i]代表这一头母牛之前有多少编号比他小的母牛的个数，其中第一肯定为0，所以直接从第二开始。求这些母球的编号排序情况

思路：线段树实现，这个使用很灵活。从后向前读取数据，第i组数据Ni[i]表示的为剩余数据的第Ni[i]+1小值。发现了第K小问题，所以可以用线段树来实现。

这个题不错，灵活运用线段树。
*/

#include <cstdio>
const int nMax=8010;
int N;
int Ni[nMax],res[nMax];
int ans;
struct Tree
{
	int l,r;
	int num;
	Tree(){num=0;}
	Tree(int l,int r,int num):l(l),r(r),num(num){}
}tree[nMax<<2];
void build(int l,int r,int rt)
{
	if(l==r)
		tree[rt]=Tree(l,r,1);
	else
	{
		int mid=(l+r)>>1;
		build(l,mid,rt<<1);
		build(mid+1,r,rt<<1 | 1);
		tree[rt]=Tree(l,r,tree[rt<<1].num+tree[rt<<1 | 1].num);
	}
}
void search(int p,int rt)
{
	tree[rt].num--;
	if(tree[rt].l==tree[rt].r)
	{
		ans=tree[rt].l;
		return;
	}
	if(p<tree[rt<<1].num)
		search(p,rt<<1);
	else
		search(p-tree[rt<<1].num,rt<<1 | 1);
}
int main()
{
	//freopen("f://data.in","r",stdin);
	scanf("%d",&N);
	Ni[0]=0;
	for(int i=1;i<N;i++)
		scanf("%d",&Ni[i]);
	build(1,N,1);
	for(int i=N-1;i>=0;i--)
	{
		search(Ni[i],1);
		res[i]=ans;
	}
	for(int i=0;i<N;i++)
		printf("%d\n",res[i]);
	return 0;
}