快速排序

快速排序算法可以说是最基本最常用的算法之一了，也是公认的最佳排序算法。虽然自己知道的基本原理是分治法，时间复杂度为O(N * logN)，是非稳定排序。平时用也就是直接调用系统提供的库函数：C/C++ 中使用sort/qsort,Java中使用Arrays.sort。久而久之，快速排序的实现越来越模糊，以至于都快忘了实现算法中的递归关系。

正好在做一道题目时，又用到了快排，顺便再把快排捡起来。

【摘抄】

快速排序(QuickSort)

1、算法思想
    　快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

（1） 分治法的基本思想
    　分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

（2）快速排序的基本思想
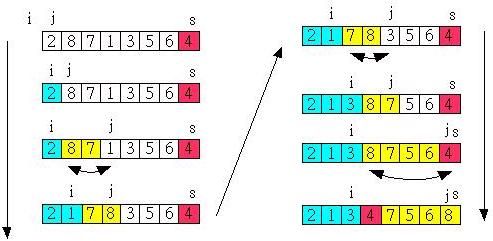
    　设当前待排序的无序区为R[low..high]，利用分治法可将快速排序的基本思想描述为：

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

	public void quick_sort(int[] a, int left, int right) {
		if(left < right){
			int pivot = partition_swap(a,left,right);
			quick_sort(a,left,pivot-1);
			quick_sort(a,pivot+1,right);
		}
	}

调用时采用：quick_sort(array,0,array.length-1);

下面展开具体的分区过程：

有两种思路，一叫“挖坑填数”，另一个叫“交换法”

挖坑填数的思路是先把a[left]存起来作为基准值，left位置就作为第一个坑。然后，从右往左遍历当遇到比基准值小的情况，则把该值填到之前的坑里，当前位置变成新坑。从左往右遍历，当遇到比基准值大的情况，同样处理。直到最后左右汇合处的坑填上基准值。

private int partition(int[] a, int left, int right) {
		int i = left;
		int j = right;
		int pos = left;
		int tar = a[left];
		while(i < j){
			while(j>i){
				if(a[j] > tar){
					j--;
				}else{
					a[pos] = a[j];
					pos = j;
					i++;
					break;
				}
			}
			while(i<j){
				if(a[i] < tar){
					i++;
				}else{
					a[pos] = a[i];
					pos = i;
					j--;
					break;
				}
			}
		}
		a[pos] = tar;
		return pos;
	}

交换法 的思路是 以a[right]作为基准值，从左向右遍历，当值大于基准值时继续向右扫描，当值小于基准值时则交换当下值与之前第一个大于基准值的值。

	private int partition_swap(int[] a, int left, int right){
		int pos = left;

		for(int i=left;i<right;i++){
			if(a[i] < a[right]){
				swap(a,pos,i);
				pos ++;
			}
		}
		swap(a,pos,right);
		return pos;
	}

	private void swap(int[] a, int x, int y) {
		int t = a[x];
		a[x] = a[y];
		a[y] = t;
	}