NMF非负矩阵分解

非负矩阵分解（Non-negative Matrix Factorization，NMF）是把一个矩阵分解成两个矩阵乘积的形式，来分解多维数据。
对于给定的矩阵 V 进行分解，分解形式如下：

V≈WH

V 是 n∗m 维度的, n 是数据的维度， m 是数据样本的数量， W 是 n∗r 维度的， H 是 r∗m 维度的，其中 r≤min{n,m}
将 VH 写成列向量的组合：
V={v1,v2,..,vi,...,vm} vi 是列向量是一条样本数据
H={h1,h2,...,hi,...,hm} hi 也是一条列向量
则：
vi=Whi
可以认为每个样本数据是 hi 的线性组合
Lee and Seung, 1999给出了求 WH 的两种方法：
第一种方法：
优化目标函数：

W,H 的迭代公式：

上面中是对矩阵中固定元素进行迭代，当整体的误差达到容许范围时候结束跌倒。
第二种方法：
优化目标函数：

W,H 的迭代公式：

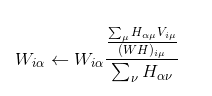
第一种方法更新利用梯度梯度下降法的更新规则如下：

当上门的更新步长 η 足够小，欧氏距离会随着迭代而减小，而当时候能够更好的达到迭代效果。
第二种方法的更新利用梯度下降法的更新规则如下：

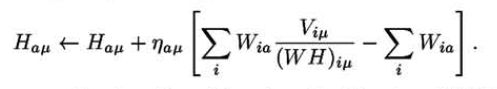
当 η 足够小的时候也能达到好的效果，当 时候效果更好。

下面利用sklearn中的ProjectedGradientNMF函数进行测试
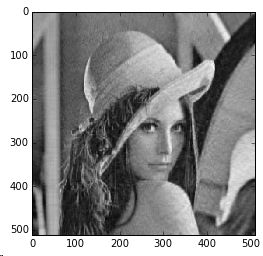
利用lena图片进行测试
原始图片

# coding=gbk
from PIL import Image
import numpy as np
# import scipy
import matplotlib.pyplot as plt
from sklearn.decomposition import ProjectedGradientNMF
def ImageToMatrix(filename):
    # 读取图片
    im = Image.open(filename)
    # 显示图片
# im.show() 
    width,height = im.size
    im = im.convert("L") 
    data = im.getdata()
    data = np.matrix(data,dtype='float')/255.0
    new_data = np.reshape(data,(width,height))
    return new_data
# new_im = Image.fromarray(new_data)
# # 显示图片
# new_im.show()
def MatrixToImage(data):
    data = data*255
    new_im = Image.fromarray(data.astype(np.uint8))
    return new_im



filename = 'lena.jpg'
data = ImageToMatrix(filename)
#print data 
new_im = MatrixToImage(data)
model = ProjectedGradientNMF(n_components = 100,init= 'nndsvda', beta=5.0,tol=5e-4)
# model.fit(data)
W = model.fit_transform(data);
H = model.components_;
plt.imshow(np.dot(W,H), cmap=plt.cm.gray, interpolation='nearest')
#new_im.show()
#new_im.save('lena_1.bmp')

当 tol=5e−3 时候复原的图片，下图有点看不懂。。。

当 tol=5e−4 时候，结果还能识别的

当 tol=5e−5 时候，结果已经很好了

下面通过多张图片看看效果如何

数据是sklearn中的400张人脸，测试时候我只是用来100张。
这里的400张照片数组，在sklearn中包里面就已经是矩阵的形式了，我将其转换成图片后，在进行处理的。
图片数据互相转换程序

# -*- coding: utf-8 -*-
import numpy as np 
import matplotlib.pyplot as plt
from PIL import Image
def ImagetoData(num=100):
    filename = 'face/face'
    data = []
    for i in range(num):
        filename = 'face/face'+ str(i) + '.jpg'
        # 读取图片
        im = Image.open(filename)
    # 显示图片
# im.show() 
        width,height = im.size
        im = im.convert("L") 
        picdata = im.getdata()
        picdata = list(picdata)
        data.append(picdata)
    data = np.matrix(data,'float')/255.0
    return data

def DatatoImage(title,Data,savename):
    w,h = np.shape(Data)
    n_col = int(w**0.5)
    n_row = n_col 
    p_size = int(h**0.5)
    plt.figure(figsize=(2*n_col,2.26*n_row))
    plt.suptitle(title,size=16)
    for i in range(w):
        plt.subplot(n_row,n_col,i+1)
        plt.imshow(Data[i,:].reshape((p_size,p_size)),
                   cmap=plt.cm.gray,
                   interpolation='nearest')
        plt.xticks(())
        plt.yticks(())
    plt.subplots_adjust(0.01, 0.05, 0.99, 0.93, 0.04, 0.)
    plt.savefig(savename)


#data = ImagetoData()
#title = 'face'
#savename='rawface.jpg'
#DatatoImage(title,data,savename)

nmf文件程序

# coding=gbk
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import ProjectedGradientNMF
from data2 import ImagetoData
from data2 import DatatoImage
from time import time  
def sklearn_nmf():
    data = ImagetoData(100)
# data = data.T 
    w,h = np.shape(data)
    n_c = 100

    print 'data shape,',np.shape(data)
    print 'n_c',n_c
# data = data.T 
    model = ProjectedGradientNMF(n_components = n_c,init= 'nndsvda', beta=5.0,tol=5e-5)
# model.fit(data)
    W = model.fit_transform(data);
    H = model.components_;
    print 'new_data shape',np.shape(H)
    print 'reconstruction_err_:',model.reconstruction_err_
# print 'n_iter_:',model.n_iter_
    title = 'NMFw'
    savename = 'result/NMFw.jpg'
    DatatoImage(title,W,savename)
    title = 'NMFh'
    savename = 'result/NMFh.jpg'
    DatatoImage(title,H,savename)
    title = 'NMFwh'
    savename = 'result/NMFwh.jpg'
    DatatoImage(title,np.dot(W,H),savename)
    for i in range(100):
        plt.imshow(H[i,:].reshape((64,64)), cmap=plt.cm.gray, interpolation='nearest')
# new_im.save('result/sklearn_nmf.bmp')
# np.savetxt('result/sklearn_nmf.txt', new_data, fmt='%3.3f',delimiter=',')
# new_im.show()
# print np.shape(new_data)
    return W,H 

t0 = time()
W,H = sklearn_nmf()
t1 = time()
t = t1 - t0
print t 

可以通过调整

ProjectedGradientNMF(n_components = n_c,init= 'nndsvda', beta=5.0,tol=5e-5)

中的 tol 实验结果是不一样，这个毕竟控制这精度的。
上面的程序，我输出了 W,H,WH 三个数据矩阵，转换成人脸的格式输出，发现:
W 矩阵只是起到系数的作用，在lee的论文中也讲到叫做基矩阵
H 矩阵输出结果就是人脸，只有前面部分人脸比较好的，后面只是人脸的基本轮廓了。这里的人脸是在原始数据中的人脸部分数据组成的人脸，例如：将A的鼻子，B的眼睛，C的嘴，组合的结果
WH 矩阵就是模拟的人脸结果，通过调节tol的值可以输出很好的效果，下面的截图 tol=5e−5 效果很好，但是时间是比较长的

原始人脸

<由于W矩阵转换成人脸照片无意义，而H矩阵的人脸很恐怖，就不截图了>

相关论文：
1.Projected Gradient Methods for Non-negative Matrix Factorization Chih-Jen Lin
2.Learning the parts of objects by non-negative matrix factorization Daniel D. Lee* & H. Sebastian Seung*†
3.Algorithms for Non-negative Matrix Factorization Daniel D. Lee* & H. Sebastian Seung*†
4.Algorithms, Initializations, and Convergence for the Nonnegative Matrix Factorization