Bayesian facerevisited : a joint formulation 学习笔记

本文转自：http://m.blog.csdn.net/blog/xp215774576/45025145

Bayesian facerevisited : a joint formulation

A joint formulation: x = u + ε

这篇论文做了以下几件事情:

1.   回顾由Baback Moghaddam 等 提出经典贝叶斯人脸识别方法。

而Face Verification 和Face identification 是人脸识别两个子问题。 

Face verification是指验证两张脸是否为同一个人。

Face identification 是指寻找一张检测的脸是谁。

这篇文章主要是Face verification 问题,而Face verification 是Face identification的基础。

经典贝叶斯人脸识别的原理：

R(x1,x2)=log   x1,x2是验证的两张脸。

Hi是假设条件为两张脸是同一个人

He是假设条件为两张脸不是同一个人

det=x1-x2,x1,x2代表人脸特征。

最后用R的比例值作为验证两张脸为同一个人的决策值。

如果两张脸是同一张脸，即在Hi条件下,det =x1-x2的值满足两张脸相同的特征的概率很大，即p大。

且He条件下，满足两张脸不同特征的概率小，

即p( 概率小，最后R值很大，我们的验证结果是两张脸是同一张脸，则决策成功。如果两张脸不是同一张脸，则相反，最后R值很小，

我们的验证结果是两张脸不是同一张脸，则决策成功。

这是两种条件分对。答案Yes.

如果两张脸是同一张脸,Hi下， 分布小概率下，即误差分为不满足同脸特征。

He下分正确，也满足不是同一张脸特征。则最后值相对小，则模糊分不清。反之，同样。这是一种条件分错。答案未知.

最后两种条件都分错.答案No。验证分错。这种概率最小。

这两种都分错的概率为误差概率。这人脸验证要通过两个关口的检验，才 最终决策。

 

如上图，class 1 代表 两种脸为同一张脸，class 2 代表两种脸不是同一张脸。

以前的贝叶斯方法是基于给定两张脸的差分X-Y模型。把两种脸的2维空间投影到一维空间。

上图所示：模型的差分X-Y等于2维空间的点投影到一维上，再验证两张脸。虽然能捕捉主要的信息，但在上图投影在原点范围是不可分的。就像上面分析的，两种条,下，有一种条件分类失败，就会让最后验证值R不确定。造成不可分Inseparable。

因此本论文，提出直接在(x1,x2)联合下建立2维模型，而且在同样的框架下-贝叶斯分类。算法的具体思路：1.求(x1,x2)的概率分布假设分高斯分布。2.模型、用EM-like算法训练参数。3.每个脸等于两个独立的潜在变量之和，不同人的脸的变化+相同人脸的变化。4.给定学习模型，我们获得联合分布(x1,x2),再log可能的闭合表达比例r,能在测试阶段获得有效的计算。

 

作者发现 联合贝叶斯方法与其他人脸验证学习方法：度量学习和基于参照模型之间的有趣联系。1.我们联合贝叶斯的相似性度量超过了马氏距离的标准形式。2.在这种新的相似性度量保持在原始特征空间上的分离，导致更好的性能。3.这种 joint Bayesian formulation 是参数形式的参照模型的一种。

 

显而易见，好的监督算法，或非监督算法,包括我们的，都需要好的训练的数据库。

这个数据库要”wide” 和”deep”,广和深。这标准的(Labeled Face in the wild ) LFW上，数据不广和深。作者提供了一种新的数据库，(WDRef).有3000subject,对象。其中2000个对象有超过15个图片，1000个对象多于40个图片)。而且，在这数据库上，还分享了两种底层存取特征。

 

这论文主要贡献：

1 Ajoint formulation of Bayesian face with an appropriate prior on the facerepresentation.

2证明joint Bayesian face 超过最先进的监督方法。

3公开了广和深的数据库

 

2.1  a naive formulation

一种天真形式： (x1,x2)概率分布假设为高斯分布，然后求P(x1,x2|Hi),p(x1,x2|He),这两种概率分布P(x1,x2|Hi)=N(0, ∑I),p(x1,x2|He)= N(0, ∑E)。再用R求两种概率的商，来验证x1,x2的相似性。 得到的结果后面验证要比传统的贝叶斯人脸好。

上面这种方法是从统计数据中，直接训练协方差矩阵∑I，∑E。有两个因素限制了贝叶斯性能：

1.数据集中样本不完全独立，这∑E不是blockwise 块对对角线出现矩阵。

2.人脸特征为d维特征，那么协方差矩阵为2d矩阵。

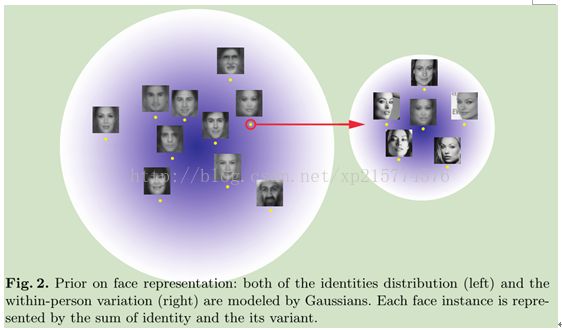
左边图：是不同人的脸变化分布，右边是同一个人的脸变化分布。

在左边是人脸都位于泡泡中间，一个人的人脸有且只有一张，高斯分布。右边人脸空间是同一个人的脸变化分布，高斯分布。左右空间是相互独立。每个人脸对象是左identity和右within-person之和。所以人脸x = u + ε.x为x1,或x2.显然,由于u, ε为高斯分布，并相反独立，所以x也是高斯分布。X1,x2有相同高斯分布，联合分布(x1,x2)也为高斯分布N(0, ∑12). ∑12=∑u+∑ε.u= N (0,S µ ).

 

u服从N (0,S µ ), ε服从N (0,S ε)，即人与人之间脸的变化(天生遗传变化),与同一个人的脸的变化(光照，姿态，表情，等)假设相互独立. 由于u与e独立高斯分布。

回顾上面两个假设Hi,He.和R(x1,x2).以上以上，(x1,x2)服从N(0,cov(x1,x2)).

cov(x1,x2)=cov(u1,u2)+cov(ε1, ε2).

x1,x2协方差cov(x1,x2)是指x1,x2相互关系，相互关系越大，协方差越大。相互关系越小，协方差越小。

Cov(u1,u2)是不同人的脸相互关系与同一个人的相互关系之后。

在P (x 1 ,x 2 |H I )下，

Modern Learning

模型主要训练S µ，S ε，来求r(x 1 ,x 2 )。S µ，S ε可以很好近似逼近。用EM-like算法。

EM-Exception Maximum用来求S µ，S ε.

EM算法，分为两步：第一步，求hidden 变量的最大期望值，寻找参数下的潜在变量最大似然估计或最大后验概率的算法。第二步，用最大期望值，来求参数。最后用参数代入第一步。循环迭代。重复迭代，直到收敛。

最大似然估计：随机抽取A,B,C,D,…, ，若抽到了A,我们说A的概率最大。写出似然函数，对似然函数取对数，求导，解似然方程（求参数）。即求极大似然估计下，使求得参数，使这样本出现的概率最大。每个样本相互独立，出现概率的乘积为似然函数，再相乘就等到总体最大似然函数，最后求让似然函数最大的参数值。

 

判别方法：直接参数判别函数，不考虑样本的生成模型，直接研究预测模型。支持向量机，决策树，最近邻。需要样本少。

生成方法：要研究概率密度函数，用样本的概率密度函数来做决策。因此需要大量样本。