POJ 1222 EXTENDED LIGHTS OUT(矩阵反转问题——枚举or高斯消元)
EXTENDED LIGHTS OUT
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 8390 | Accepted: 5422 |
Description
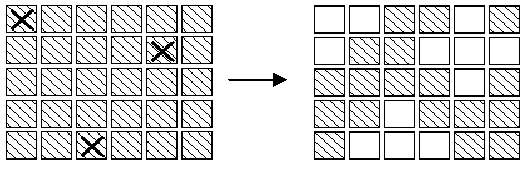
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
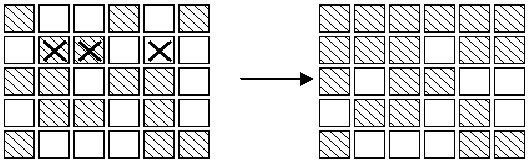
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.

The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.

Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0
Sample Output
PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1
题意:有一个5*6的矩阵,每一位是0或者1。 没翻转一位,它的上下左右的数字也为改变。(0变成1,1变成0)。要把矩阵中所有的数都变成0。求最少翻转次数的方案,输出矩阵(需要翻转的地方用1表示,反则用0表示)。
同样问题:POJ3279
题解:
①枚举法:枚举第一行的可能,在底下4行中,对于每个数,它上面的数是1,则需要翻转,反之不需要。这样就可以通过枚举第一行的办法,解决问题。
代码如下:
#include<cstdio>
#include<cstring>
int map[10][10];
int opt[10][10];//保存最优方案
int flip[10][10];//保存中间结果
int dir[5][2]={{1,0},{-1,0},{0,0},{0,1},{0,-1}};
int judge(int x,int y)//查询(x,y)的颜色
{
int i,c=map[x][y];
for(i=0;i<5;++i)
{
int x2=x+dir[i][0];
int y2=y+dir[i][1];
if(0<=x2&&x2<5&&0<=y2&&y2<6)
c+=flip[x2][y2];
}
return c%2;
}
int calc()
{
int i,j,res;
for(i=1;i<5;++i)
{
for(j=0;j<6;++j)
{
if(judge(i-1,j)!=0)//上方格子是1,则必须翻转(i,j)号格子
flip[i][j]=1;
}
}
for(i=0;i<6;++i)//判断最后一行是否全部是0
{
if(judge(4,i)!=0)//当前方案不可行
return -1;
}
res=0;
for(i=0;i<5;++i)
{
for(j=0;j<6;++j)
{
if(flip[i][j])//统计当前方案需要翻转的次数
res++;
}
}
return res;
}
int main()
{
int t,i,j,ans,num,k=1;
scanf("%d",&t);
while(t--)
{
for(i=0;i<5;++i)
{
for(j=0;j<6;++j)
scanf("%d",&map[i][j]);
}
ans=-1;
//按照字典序枚举第一行所有的可能,方案数为2^6
for(i=0;i< 1<<6;++i)
{
memset(flip,0,sizeof(flip));
for(j=0;j<6;++j)
flip[0][5-j]=i>>j&1;
num=calc();
if(num>=0&&(ans<0||ans>num))
{
ans=num;
memcpy(opt,flip,sizeof(flip));//把flib数组复制给opt数组
}
}
printf("PUZZLE #%d\n",k++);
for(i=0;i<5;++i)
{
for(j=0;j<5;++j)
printf("%d ",opt[i][j]);
printf("%d\n",opt[i][j]);
}
}
return 0;
}
②高斯消元法:可以运用异或关系来构建矩阵。我们用a[i][j]表示目标格子当前的状态,把x[i][j]表示对这个格子的操作(1表示翻转,0表示不翻转) 对于每个0<i<5 && 0<j<6的格子都有:
x[i-1][j]^x[i+1][j]^x[i][j-1]^x[i][j+1]^ x[i][j]^a[i][j]=0; 对两边同时异或a[i][j]得到
x[i-1][j]^x[i+1][j]^x[i][j-1]^x[i][j+1]^ x[i][j]=a[i][j]。
这样我们就可以联立方程组要求解。一共30个方程组,30个自由元。
代码如下:
//高斯消元法:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int equ,var;//equ个方程,var个自由元
int a[32][32];//增广矩阵
int x[32];//保存解
void init_A()
{
memset(a,0,sizeof(a));
equ=30; var=30;
for(int i=0;i<5;++i)//合理存在的系数全部初始化为1
{
for(int j=0;j<6;++j)
{
a[i*6+j][i*6+j]=1;
if(i>0)
a[i*6+j][(i-1)*6+j]=1;
if(j>0)
a[i*6+j][i*6+j-1]=1;
if(i<4)
a[i*6+j][(i+1)*6+j]=1;
if(j<5)
a[i*6+j][i*6+j+1]=1;
}
}
for(int i=0;i<30;++i)
scanf("%d",&a[i][30]);
}
void Gauss()
{
int k,max_r,col;
for(k=0,col=0; k<equ&&col<var; ++k,++col)
{
max_r=k;
//列主元法
//找第col个自由元系数绝对值最大的行i(i > k) 与 当前行(k行)交换
for(int i=k+1;i<equ;++i)
{
if(a[i][col]>a[max_r][col])
max_r=i;
}
if(max_r!=k)//找到——交换
{
for(int i=col;i<=var;++i)
swap(a[k][i],a[max_r][i]);
}
if(a[k][col]==0)// 说明该col列第k行以下全是0了,则处理当前行的下一列.
{
k--;
continue;
}
for(int i=k+1;i<=equ;++i)//枚举要删去的行
{
if(a[i][col]!=0)
{
for(int j=col;j<=var;++j)
a[i][j]^=a[k][j];
}
}
}
for(int i=var-1; i>=0; --i)//得到三角矩阵,回代求解
{
x[i]=a[i][var];
for(int j=i+1;j<var;++j)
x[i]^=(a[i][j]*x[j]);
}
}
int main()
{
int t,i,k=1;
scanf("%d",&t);
while(t--)
{
init_A();
Gauss();
printf("PUZZLE #%d\n",k++);
for(i=0;i<30;++i)
{
if((i+1)%6==0)
printf("%d\n",x[i]);
else
printf("%d ",x[i]);
}
}
return 0;
}