基数排序
基数排序介绍
基数排序(Radix Sort)是桶排序的扩展,它的基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。
具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
基数排序图文说明
基数排序图文说明
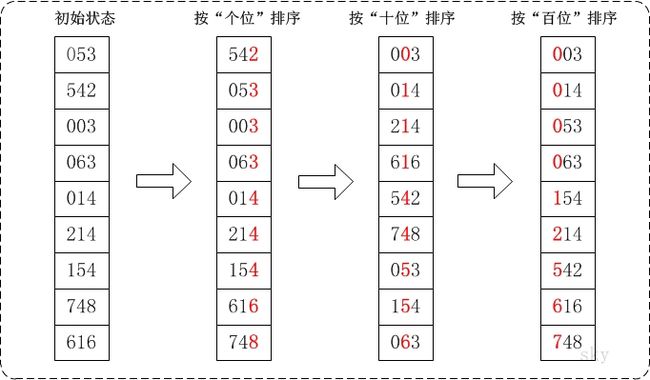
通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616},它的示意图如下:
在上图中,首先将所有待比较树脂统一为统一位数长度,接着从最低位开始,依次进行排序。
1. 按照个位数进行排序。
2. 按照十位数进行排序。
3. 按照百位数进行排序。
排序后,数列就变成了一个有序序列。
基数排序代码
/* * 获取数组a中最大值 * * 参数说明: * a -- 数组 * n -- 数组长度 */
int get_max(int a[], int n)
{
int i, max;
max = a[0];
for (i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
return max;
}
/* * 对数组按照"某个位数"进行排序(桶排序) * * 参数说明: * a -- 数组 * n -- 数组长度 * exp -- 指数。对数组a按照该指数进行排序。 * * 例如,对于数组a={50, 3, 542, 745, 2014, 154, 63, 616}; * (01) 当exp=1表示按照"个位"对数组a进行排序 * (02) 当exp=10表示按照"十位"对数组a进行排序 * (03) 当exp=100表示按照"百位"对数组a进行排序 * ... */
void count_sort(int a[], int n, int exp)
{
int output[n]; // 存储"被排序数据"的临时数组
int i, buckets[10] = {0};
// 将数据出现的次数存储在buckets[]中
for (i = 0; i < n; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (i = n - 1; i >= 0; i--)
{
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (i = 0; i < n; i++)
a[i] = output[i];
}
/* * 基数排序 * * 参数说明: * a -- 数组 * n -- 数组长度 */
void radix_sort(int a[], int n)
{
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = get_max(a, n); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
count_sort(a, n, exp);
}radix_sort(a, n)的作用是对数组a进行排序。
1. 首先通过get_max(a)获取数组a中的最大值。获取最大值的目的是计算出数组a的最大指数。
获取到数组a中的最大指数之后,再从指数1开始,根据位数对数组a中的元素进行排序。排序的时候采用了桶排序。
count_sort(a, n, exp)的作用是对数组a按照指数exp进行排序。
下面简单介绍一下对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}按个位数进行排序的流程。
(01) 个位的数值范围是[0,10)。因此,参见桶数组buckets[],将数组按照个位数值添加到桶中。
(02) 接着是根据桶数组buckets[]来进行排序。假设将排序后的数组存在output[]中;找出output[]和buckets[]之间的联系就可以对数据进行排序了。
基数排序实现
基数排序C实现
实现代码(radix_sort.c)
/**
* 基数排序:C 语言
*
* @author skywang
* @date 2014/03/15
*/
#include <stdio.h>
// 数组长度
#define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )
/*
* 获取数组a中最大值
*
* 参数说明:
* a -- 数组
* n -- 数组长度
*/
int get_max(int a[], int n)
{
int i, max;
max = a[0];
for (i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
return max;
}
/*
* 对数组按照"某个位数"进行排序(桶排序)
*
* 参数说明:
* a -- 数组
* n -- 数组长度
* exp -- 指数。对数组a按照该指数进行排序。
*
* 例如,对于数组a={50, 3, 542, 745, 2014, 154, 63, 616};
* (01) 当exp=1表示按照"个位"对数组a进行排序
* (02) 当exp=10表示按照"十位"对数组a进行排序
* (03) 当exp=100表示按照"百位"对数组a进行排序
* ...
*/
void count_sort(int a[], int n, int exp)
{
int output[n]; // 存储"被排序数据"的临时数组
int i, buckets[10] = {0};
// 将数据出现的次数存储在buckets[]中
for (i = 0; i < n; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (i = n - 1; i >= 0; i--)
{
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (i = 0; i < n; i++)
a[i] = output[i];
}
/*
* 基数排序
*
* 参数说明:
* a -- 数组
* n -- 数组长度
*/
void radix_sort(int a[], int n)
{
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = get_max(a, n); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
count_sort(a, n, exp);
}
void main()
{
int i;
int a[] = {53, 3, 542, 748, 14, 214, 154, 63, 616};
int ilen = LENGTH(a);
printf("before sort:");
for (i=0; i<ilen; i++)
printf("%d ", a[i]);
printf("\n");
radix_sort(a, ilen);
printf("after sort:");
for (i=0; i<ilen; i++)
printf("%d ", a[i]);
printf("\n");
}基数排序C++实现
实现代码(RadixSort.cpp)
/** * 基数排序:C++ * * @author skywang * @date 2014/03/15 */
#include<iostream>
using namespace std;
/* * 获取数组a中最大值 * * 参数说明: * a -- 数组 * n -- 数组长度 */
int getMax(int a[], int n)
{
int i, max;
max = a[0];
for (i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
return max;
}
/* * 对数组按照"某个位数"进行排序(桶排序) * * 参数说明: * a -- 数组 * n -- 数组长度 * exp -- 指数。对数组a按照该指数进行排序。 * * 例如,对于数组a={50, 3, 542, 745, 2014, 154, 63, 616}; * (01) 当exp=1表示按照"个位"对数组a进行排序 * (02) 当exp=10表示按照"十位"对数组a进行排序 * (03) 当exp=100表示按照"百位"对数组a进行排序 * ... */
void countSort(int a[], int n, int exp)
{
int output[n]; // 存储"被排序数据"的临时数组
int i, buckets[10] = {0};
// 将数据出现的次数存储在buckets[]中
for (i = 0; i < n; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (i = n - 1; i >= 0; i--)
{
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (i = 0; i < n; i++)
a[i] = output[i];
}
/* * 基数排序 * * 参数说明: * a -- 数组 * n -- 数组长度 */
void radixSort(int a[], int n)
{
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = getMax(a, n); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
countSort(a, n, exp);
}
int main()
{
int i;
int a[] = {53, 3, 542, 748, 14, 214, 154, 63, 616};
int ilen = (sizeof(a)) / (sizeof(a[0]));
cout << "before sort:";
for (i=0; i<ilen; i++)
cout << a[i] << " ";
cout << endl;
radixSort(a, ilen); // 基数排序
cout << "after sort:";
for (i=0; i<ilen; i++)
cout << a[i] << " ";
cout << endl;
return 0;
}基数排序Java实现
实现代码(RadixSort.java)
/** * 基数排序:Java * * @author skywang * @date 2014/03/15 */
public class RadixSort {
/* * 获取数组a中最大值 * * 参数说明: * a -- 数组 * n -- 数组长度 */
private static int getMax(int[] a) {
int max;
max = a[0];
for (int i = 1; i < a.length; i++)
if (a[i] > max)
max = a[i];
return max;
}
/* * 对数组按照"某个位数"进行排序(桶排序) * * 参数说明: * a -- 数组 * exp -- 指数。对数组a按照该指数进行排序。 * * 例如,对于数组a={50, 3, 542, 745, 2014, 154, 63, 616}; * (01) 当exp=1表示按照"个位"对数组a进行排序 * (02) 当exp=10表示按照"十位"对数组a进行排序 * (03) 当exp=100表示按照"百位"对数组a进行排序 * ... */
private static void countSort(int[] a, int exp) {
//int output[a.length]; // 存储"被排序数据"的临时数组
int[] output = new int[a.length]; // 存储"被排序数据"的临时数组
int[] buckets = new int[10];
// 将数据出现的次数存储在buckets[]中
for (int i = 0; i < a.length; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (int i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (int i = a.length - 1; i >= 0; i--) {
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (int i = 0; i < a.length; i++)
a[i] = output[i];
output = null;
buckets = null;
}
/* * 基数排序 * * 参数说明: * a -- 数组 */
public static void radixSort(int[] a) {
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = getMax(a); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
countSort(a, exp);
}
public static void main(String[] args) {
int i;
int a[] = {53, 3, 542, 748, 14, 214, 154, 63, 616};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
radixSort(a); // 基数排序
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}上面3种实现的原理和输出结果都是一样的。下面是它们的输出结果:
before sort:53 3 542 748 14 214 154 63 616
after sort:3 14 53 63 154 214 542 616 748 转载自:基数排序