深度学习入门笔记(二):神经网络基础
专栏——深度学习入门笔记
声明
1)该文章整理自网上的大牛和机器学习专家无私奉献的资料,具体引用的资料请看参考文献。
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)博主才疏学浅,文中如有不当之处,请各位指出,共同进步,谢谢。
4)此属于第一版本,若有错误,还需继续修正与增删。还望大家多多指点。大家都共享一点点,一起为祖国科研的推进添砖加瓦。
文章目录
- 专栏——深度学习入门笔记
- 声明
- 深度学习入门笔记(二):神经网络基础
- 1、二分类
- 2、逻辑回归
- 3、逻辑回归的代价函数
- 4、梯度下降法
- 梯度下降法可以做什么?
- 梯度下降法的形象化说明
- 梯度下降法的细节化说明
- 梯度下降法的具体化说明
- 5、逻辑回归的梯度下降
- 6、m 个样本的梯度下降
- 推荐阅读
- 参考文章
深度学习入门笔记(二):神经网络基础
1、二分类
下面要学习的是神经网络的基础知识,其中需要注意的是,当实现一个神经网络的时候,需要知道一些非常重要的技术和技巧,闲言少叙,直接开搞。
逻辑回归(logistic regression) 是一个用于 二分类(binary classification) 的算法。首先从一个问题——猫咪识别开始说起,如果识别这张图片为猫,则输出标签1作为结果;如果识别出不是猫,那么输出标签0作为结果。用字母 y y y 来表示输出的结果标签,如下图所示:

如上图所示,一张图片在计算机中对应三个矩阵,分别对应图片中的红、绿、蓝三种颜色通道,且图片大小与三个矩阵相同,分别对应图片中红、绿、蓝三种像素的强度值。
为了把这些像素值转换为 特征向量 x x x,需要定义特征向量表示图片,把像素都取出来,也就是矩阵中的数据,例如255、231等等,取完红色像素接着是绿色像素,最后是蓝色像素,直到得到特征向量,也就是图片中红、绿、蓝像素排列的值。如果图片的大小为64x64像素,那么 x x x 的总维度,是64 * 64 * 3,也即是三个像素矩阵中的像素总量(12288)。
现在用 n x = 12288 n_x=12288 nx=12288 来表示输入特征向量的维度,有时为了简洁,直接用小写的 n n n 来表示。所以二分类问题中,最终的目标就是习得一个分类器,以图片特征向量作输入,预测输出结果 y y y 是1还是0,即预测图片中是否有猫。
符号定义 :
x x x:表示一个 n x n_x nx 维数据,为输入数据,维度为 ( n x , 1 ) (n_x,1) (nx,1);
y y y:表示输出结果,取值为 ( 0 , 1 ) (0,1) (0,1);
( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)):表示第 i i i 组数据,可能是训练数据,也可能是测试数据,此处默认为训练数据;
X = [ x ( 1 ) , x ( 2 ) , . . . , x ( m ) ] X=[x^{(1)},x^{(2)},...,x^{(m)}] X=[x(1),x(2),...,x(m)]:表示所有的训练数据集的输入值,放在一个 n x × m n_x×m nx×m 的矩阵中,其中 m m m 表示样本数目;
Y = [ y ( 1 ) , y ( 2 ) , . . . , y ( m ) ] Y=[y^{(1)},y^{(2)},...,y^{(m)}] Y=[y(1),y(2),...,y(m)]:对应表示所有训练数据集的输出值,维度为 1 × m 1×m 1×m。
2、逻辑回归
对于二元分类问题,给定输入特征向量 X X X,它可能对应一张图片,如果想识别这张图片是否是猫的图片,怎么做?
定义算法的输出预测为 y ^ \hat{y} y^,也就是对实际值 y y y 的估计。更正式地来说, y ^ \hat{y} y^ 表示 y y y 等于1的一种可能性或者是几率,当然,前提条件是给定了输入特征 X X X。
上面说过 X X X 是一个 n x n_x nx 维的向量,相当于有 n x n_x nx 个特征的特征向量。 w w w 表示逻辑回归的参数,也是一个 n x n_x nx 维向量,因为 w w w 实际上是 特征权重,维度与特征向量相同。参数里面还有 b b b,是一个实数,表示偏差。所以给出输入以及参数后,一个可以尝试却不可行的结果是 y ^ = w T x + b \hat{y}={{w}^{T}}x+b y^=wTx+b。
为什么说可以尝试,却不可行呢?注意,这时得到的实际上是线性回归时用到的一个关于输入 x x x 的线性函数,但这对二元分类问题来讲,却不是一个非常好的算法。因为 y ^ \hat{y} y^ 表示实际值 y y y 等于1的几率,也就是说 y ^ \hat{y} y^ 应该在0到1之间。
这是一个需要解决的问题,因为 w T x + b {{w}^{T}}x+b wTx+b 可能比1要大得多,更有甚者,可能是一个负值,但是我们想要的是一个概率。因此,在逻辑回归中,输出是 y ^ \hat{y} y^ 作为自变量的 sigmoid 函数的输出值。有点绕,其实简单来说, y ^ = s i g m o i d ( y ) \hat{y} = sigmoid(y) y^=sigmoid(y)。
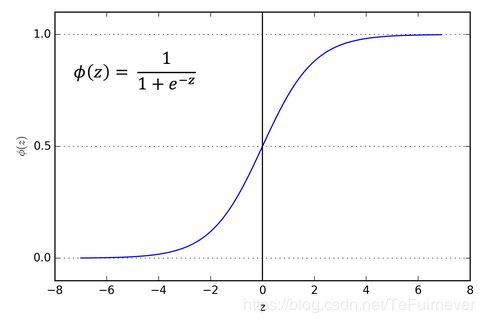
如上图所示,就是 sigmoid 函数的图像,它平滑地从0走向1,这里的作用其实还是把线性函数转换为非线性函数。
关于 sigmoid 函数的公式是这样的
σ ( z ) = 1 1 + e − z \sigma \left( z \right)=\frac{1}{1+{{e}^{-z}}} σ(z)=1+e−z1
这里要注意的是,从图像可以看出两点:
- 如果 z z z 非常大,那么 e − z {{e}^{-z}} e−z 将会接近于0, σ ( z ) \sigma \left( z \right) σ(z) 会非常接近1。
- 相反地,如果 z z z 非常小或者一个绝对值很大的负数,那么 e − z {{e}^{-z}} e−z 会变得很大, σ ( z ) \sigma \left( z \right) σ(z) 就接近于0。
因此当实现逻辑回归时, y ^ \hat{y} y^ 在0到1之间,成为对 y = 1 y=1 y=1 概率的一个很好的估计。
3、逻辑回归的代价函数
为什么需要代价函数(也翻译作成本函数)?
为了训练逻辑回归模型,得到参数 w w w和参数 b b b。
看到这里你可能有点蒙逼,先来看一下损失函数吧,你可能会问那 什么是损失函数? 损失函数又叫做 误差函数,用来衡量算法的运行情况,Loss function: L ( y ^ , y ) L\left( \hat{y},y \right) L(y^,y).。通过这个 L L L,也就是损失函数,来衡量预测输出值和实际值有多接近。
一般的损失函数有预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中不这么做,为什么?因为在学习逻辑回归参数时,会发现优化目标不是 凸优化(在凸优化中局部最优值必定是全局最优值),只能找到多个局部最优值,很可能找不到全局最优值。所以虽然平方差是一个不错的损失函数,但在逻辑回归模型中定义的是另外一个损失函数,即
L ( y ^ , y ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) L\left( \hat{y},y \right)=-y\log(\hat{y})-(1-y)\log (1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^)
为什么要用这个函数作为逻辑损失函数?来举两个例子你就懂了,首先确定一件事,无论解决什么问题,你肯定想要误差尽可能地小。好了,现在来看例子吧:
-
当 y = 1 y=1 y=1 时损失函数 L = − log ( y ^ ) L=-\log (\hat{y}) L=−log(y^),如果想要损失函数 L L L 尽可能得小,那么 y ^ \hat{y} y^ 就要尽可能大,因为 sigmoid 函数取值 [ 0 , 1 ] [0,1] [0,1],所以 y ^ \hat{y} y^ 会无限接近于1。
-
当 y = 0 y=0 y=0 时损失函数 L = − log ( 1 − y ^ ) L=-\log (1-\hat{y}) L=−log(1−y^),如果想要损失函数 L L L 尽可能得小,那么 y ^ \hat{y} y^ 就要尽可能小,因为 sigmoid 函数取值 [ 0 , 1 ] [0,1] [0,1],所以 y ^ \hat{y} y^ 会无限接近于0。
而在逻辑回归中,我们期待的输出就是1或者0,是不是这个损失函数更好呢?
可以看出来,损失函数是在单个训练样本中定义的,它衡量的是算法在单个训练样本中表现如何。那么怎么衡量算法在全部训练样本上的表现如何?
需要定义一个算法的 代价函数,算法的代价函数,是对 m m m 个样本的损失函数求和,然后除以 m m m:
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = 1 m ∑ i = 1 m ( − y ( i ) log y ^ ( i ) − ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ) J\left( w,b \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{L\left( {{{\hat{y}}}^{(i)}},{{y}^{(i)}} \right)}=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( -{{y}^{(i)}}\log {{{\hat{y}}}^{(i)}}-(1-{{y}^{(i)}})\log (1-{{{\hat{y}}}^{(i)}}) \right)} J(w,b)=m1i=1∑mL(y^(i),y(i))=m1i=1∑m(−y(i)logy^(i)−(1−y(i))log(1−y^(i)))
在训练逻辑回归模型时,找到合适的 w w w 和 b b b,来让代价函数 J J J 的总代价降到最低即为所求。
4、梯度下降法
梯度下降法可以做什么?
在测试集上,通过最小化 代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 来训练的参数 w w w 和 b b b。
梯度下降法的形象化说明

在这个图中,横轴表示空间参数 w w w 和 b b b,代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 是曲面,因此曲面高度就是 J ( w , b ) J(w,b) J(w,b) 在某一点的函数值。
而深度学习的最终目标就是找到代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 函数值为最小值时对应的参数 w w w 和 b b b。梯度下降 可以分为三个步骤:
1. 随机初始化两个参数
以如图小红点的坐标来初始化参数 w w w 和 b b b。

开始寻找代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 函数值的最小值。
2. 朝最陡的下坡方向走一步,不断地迭代
朝最陡的下坡方向走一步,如图,走到了如图中第二个小红点处。

可能停在这里,也有可能继续朝最陡的下坡方向再走一步,如图,经过两次迭代走到第三个小红点处。
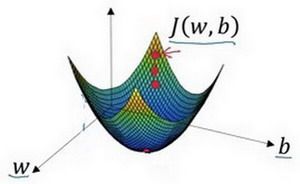
3.直到走到全局最优解或者接近全局最优解的地方
通过重复以上的步骤,可以找到全局最优解,也就是代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 这个凸函数的最小值点。
梯度下降法的细节化说明
逻辑回归的代价函数(成本函数) J ( w , b ) J(w,b) J(w,b) 是含有两个参数的。
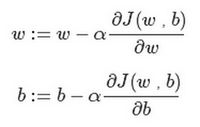
简要说明一下式子中的符号, ∂ \partial ∂ 表示求偏导符号,可以读作 round; ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 就是函数 J ( w , b ) J(w,b) J(w,b) 对 w w w 求偏导,在代码中为 d w dw dw; ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 就是函数 J ( w , b ) J(w,b) J(w,b)对 b b b 求偏导,在代码中为 d b db db。
其实无论是 d d d 还是 ∂ \partial ∂ 都是求导数的意思,那么二者的区别是什么呢?
- d d d 用在 求导数(derivative),即函数只有一个参数
- ∂ \partial ∂ 用在 求偏导(partial derivative),即函数含有两个以上的参数
梯度下降法的具体化说明
梯度下降是如何进行的呢?这里任选一参数 w w w 进行举例:假定代价函数(成本函数) J ( w ) J(w) J(w) 只有一个参数 w w w,即用一维曲线代替多维曲线,这样可以更好画出如下图像。
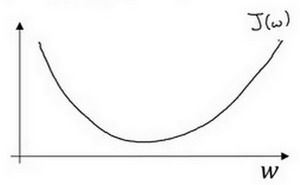
迭代就是不断重复做如图的公式:

其中,:= 表示更新参数; a a a 表示 学习率(learning rate),用来控制 步长(step); d J ( w ) d w \frac{dJ(w)}{dw} dwdJ(w) 就是函数 J ( w ) J(w) J(w) 对 w w w 求导(derivative),在代码中为 d w dw dw。对于导数更加形象化的理解就是 斜率(slope)。
如图该点的导数就是这个点相切于 J ( w ) J(w) J(w) 的小三角形的高除宽(这是高中数学学过的,不会的去百度——导数)。假设初始化如图点为起始点,该点处的斜率的符号是正,即 d J ( w ) d w > 0 \frac{dJ(w)}{dw}>0 dwdJ(w)>0,所以接下来会向左走一步(假设该点处的斜率的符号是负的,则会向右走一步),如图:

不断地向左走,直至逼近最小值点,这就是梯度下降法的迭代过程。
5、逻辑回归的梯度下降
逻辑回归的梯度下降算法,关键点是几个重要公式,虽然使用计算图来计算逻辑回归的梯度下降算法有点大材小用了,具体什么是导数,什么是计算图,可以看这个博客——深度学习入门笔记(三):数学基础之求导数。
下面来完完整整地进行这个梯度下降算法的过程演示,相信我,跟着你就能全懂了。
假设,单个样本样本只有两个特征 x 1 {{x}_{1}} x1 和 x 2 {{x}_{2}} x2,为了计算 z z z,需要输入参数 w 1 {{w}_{1}} w1、 w 2 {{w}_{2}} w2 和 b b b。
因此 z = w 1 x 1 + w 2 x 2 + b z={{w}_{1}}{{x}_{1}}+{{w}_{2}}{{x}_{2}}+b z=w1x1+w2x2+b。
回想一下逻辑回归的公式定义如下: y ^ = a = σ ( z ) \hat{y}=a=\sigma (z) y^=a=σ(z),其中 z = w T x + b z={{w}^{T}}x+b z=wTx+b、 σ ( z ) = 1 1 + e − z \sigma \left( z \right)=\frac{1}{1+{{e}^{-z}}} σ(z)=1+e−z1。
损失函数 L ( y ^ ( i ) , y ( i ) ) = − y ( i ) log y ^ ( i ) − ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) L( {{{\hat{y}}}^{(i)}},{{y}^{(i)}})=-{{y}^{(i)}}\log {{\hat{y}}^{(i)}}-(1-{{y}^{(i)}})\log (1-{{\hat{y}}^{(i)}}) L(y^(i),y(i))=−y(i)logy^(i)−(1−y(i))log(1−y^(i))。
代价函数 J ( w , b ) = 1 m ∑ i m L ( y ^ ( i ) , y ( i ) ) J\left( w,b \right)=\frac{1}{m}\sum\nolimits_{i}^{m}{L( {{{\hat{y}}}^{(i)}},{{y}^{(i)}})} J(w,b)=m1∑imL(y^(i),y(i))。
若只考虑单个样本,代价函数变为 L ( a , y ) = − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) L(a,y)=-(y\log (a)+(1-y)\log (1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))。
梯度下降法中 w w w 和 b b b 的修正表达为 w : = w − a ∂ J ( w , b ) ∂ w w:=w-a \frac{\partial J(w,b)}{\partial w} w:=w−a∂w∂J(w,b), b : = b − a ∂ J ( w , b ) ∂ b b:=b-a\frac{\partial J(w,b)}{\partial b} b:=b−a∂b∂J(w,b)。
现在画出表示这个计算过程的计算图,如下:

有了计算图,就不需要再写出公式了,只需修改参数 w w w 和 b b b。前面已经讲解了前向传播,现在来说一下反向传播。
想要计算出代价函数 L ( a , y ) L(a,y) L(a,y) 的导数,可以使用链式法则。
首先计算出 L ( a , y ) L(a,y) L(a,y) 关于 a a a 的导数。通过计算可以得出
d L ( a , y ) d a = − y / a + ( 1 − y ) / ( 1 − a ) \frac{dL(a,y)}{da}=-y/a+(1-y)/(1-a) dadL(a,y)=−y/a+(1−y)/(1−a)
而
d a d z = a ⋅ ( 1 − a ) \frac{da}{dz}=a\cdot (1-a) dzda=a⋅(1−a)
因此将这两项相乘,得到:
d z = d L ( a , y ) d z = d L d z = ( d L d a ) ⋅ ( d a d z ) = ( − y a + ( 1 − y ) ( 1 − a ) ) ⋅ a ( 1 − a ) = a − y {dz} = \frac{{dL}(a,y)}{{dz}} = \frac{{dL}}{{dz}} = \left( \frac{{dL}}{{da}} \right) \cdot \left(\frac{{da}}{{dz}} \right) = ( - \frac{y}{a} + \frac{(1 - y)}{(1 - a)})\cdot a(1 - a) = a - y dz=dzdL(a,y)=dzdL=(dadL)⋅(dzda)=(−ay+(1−a)(1−y))⋅a(1−a)=a−y
肯定会有小伙伴说自己不太会微积分,不知道链式法则。Don‘t worry!!!只需知道 d z = ( a − y ) dz=(a-y) dz=(a−y) 已经计算好了,拿来主义,直接拿过来用就可以了。
最后一步反向推导,也就是计算 w w w 和 b b b 变化对代价函数 L L L 的影响
d w 1 = x 1 ⋅ d z d{{w}_{1}}={{x}_{1}}\cdot dz dw1=x1⋅dz
d w 2 = x 2 ⋅ d z d{{w}_{\text{2}}}={{x}_{2}}\cdot dz dw2=x2⋅dz
d b = d z db=dz db=dz
然后更新
w 1 = w 1 − a d w 1 {{w}_{1}}={{w}_{1}}-a d{{w}_{1}} w1=w1−adw1
w 2 = w 2 − a d w 2 {{w}_{2}}={{w}_{2}}-a d{{w}_{2}} w2=w2−adw2
b = b − α d b b=b-\alpha db b=b−αdb
这就是单个样本实例的梯度下降算法中参数更新一次的步骤,深度学习的过程可以简单理解为重复迭代优化的过程(肯定不准确,就是为了先理解一下而已)。吴恩达老师画的图,直观的体现了整个过程:

6、m 个样本的梯度下降
我们想要的,肯定不是单个样本,而是在 m m m 个训练样本上,也就是训练集上。
首先,关于算法的带求和的全局代价函数 J ( w , b ) J(w,b) J(w,b) 的定义如下:
J ( w , b ) = 1 m ∑ i = 1 m L ( a ( i ) , y ( i ) ) J(w,b)=\frac{1}{m}\sum\limits_{i=1}^{m}{L({{a}^{(i)}},{{y}^{(i)}})} J(w,b)=m1i=1∑mL(a(i),y(i))
实际上是1到 m m m 项各个损失的平均,所以对 w 1 {{w}_{1}} w1 的微分,对 w 1 {{w}_{1}} w1 的微分,也同样是各项损失对 w 1 {{w}_{1}} w1 微分的平均。
吴恩达老师手写稿如下:

而代价函数对权重向量 θ θ θ 求导过程如下,损失函数为交叉熵损失函数,整个过程如下:

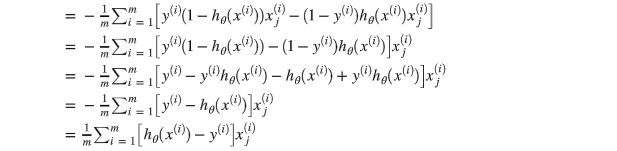
通过 向量化 就可以得到
![]()
因此更新公式为:
![]()
推荐阅读
- 深度学习入门笔记(一):深度学习引言
- 深度学习入门笔记(三):求导和计算图
- 深度学习入门笔记(四):向量化
参考文章
- 吴恩达——《神经网络和深度学习》视频课程