【NOI2017】数字格
Description
菁菁堂有一块数字格,那是王解体最喜欢去的地方。
传说中,这条气势磅礴的数字格,有N行N列,每一个格子里均有一个数。
敢于挑战自己的王解体决定来挑战这道通过率为百分之九十九的题目。
格子的第一行及第一列均是给定的:
F[k,1]=lk
F[1,k]=tk
对于其他格子,满足递推式:
F[i,j]=a*F[i,j-1]+b*F[i-1,j]+c
不出所料,当王解体能得到 F[n,n](mod 1000003)时,通过率将达到百分之百。
Solution
这道题可以用FFT打,但是我不会(……),所以用了另外一种巧妙的方法。
首先通过比较暴力的公式推导可以发现,特殊项的贡献是可以直接算出来的,而常数项c的解决会有一些麻烦,我们先把不含c的算出来,在推导c的贡献时,可以从系数入手,最左上角的c的系数肯定是1,向右拓展时是a的幂,向下拓展时是b的幂。由于每一个格子的数受它的上面和左边的数影响,若是斜向来看,每一斜列的系数和是上一列的(a+b)倍。(详见图,a=3,b=5时)
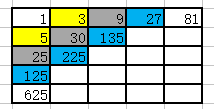
黄色块的和为: 1∗(3+5) ,灰色块的和为: 1∗(3+5)2 ,蓝色块的和为: 1∗(3+5)3 。
但是当超过对角线时,就会有两块多余的被计入系数和中(图中的绿块为多余块)。

怎么减去呢?我们可以发现实际上就等于灰色块对下一斜列的贡献,灰色块的计算是很容易的,这里就不推导了,用组合数再乘上a的幂和b的幂就可以了。最后c的贡献就是矩阵的系数和乘上c。
Code
#include