炸僵尸
题目描述
妈妈得知小星星成功地解决了买玩具难题,奖励他去看电影《生化危机 6》, 小星星看 着看着就替女主角担心起来了,因为她要对付那么多的僵尸怪物,小星星恨不得扔颗炸弹消 除可恶的僵尸们,他脑袋里开始构思出这样的场景:
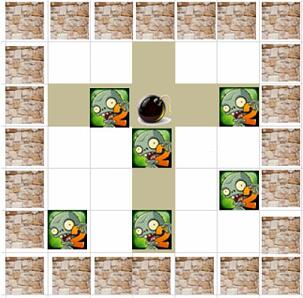
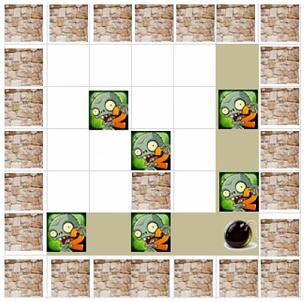
在一个 N 行 M 列单元格构成的地图中,去放置一个炸弹,这种炸弹威力巨大,以放置 点为中心进行行列延伸炸到同行同列的僵尸,但不能穿墙。上图中可以把炸弹放置在第 3 行第 4 列,最多可以炸到 4 个僵尸,如果对地图稍加改动(如下图),在第 5 行第 4 列处加 入一个墙体,又如何呢?答案还是最多炸到 4 个僵尸,只不过最佳炸弹放置点发生了变化, 应该放到第 6 行第 6 列的位置。
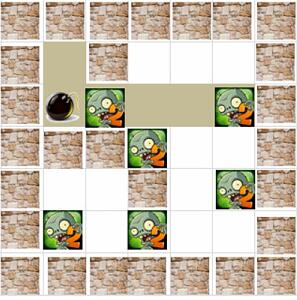
当然炸弹要靠勇敢的小星星去放,他只能在地图中朝上下左右四个方向行进(不能斜对 角移动) ,他不能穿墙,也不能穿越僵尸,要保证他的安全,如下图,告诉你小星星起始位 置是第 2 行第 2 列,那么他的最佳放置炸弹位置应该是第 3 行第 2 列,最多炸到 2 个僵尸。
现在请聪明的你也一起加入到消除僵尸的队伍来。
输入
第一行四个用空格隔开的正整数表示 N,M,X,Y,分别表示 N 行 M 列的地图,小星星起 始位置第 X 行,第 Y 列。接下来 N 行 M 列用来描述地图上每个单元格,‘ G’表示僵尸,‘#’表示墙体,只有‘.’ 表示的单元格才是小星星能够正常行走,能够放置炸弹的单元格。(数据保证四面都是墙体, 也就是第 1 行、第 N 行、第 1 列、第 M 列肯定都是墙体)。
输出
一个整数,最多能炸掉的僵尸数量。
样例输入
13 13 4 2
#
..GG#GGG.
.#G#G#G#G
…….#..G
G#.###.#G#G
13 13 4 2
#
..GG#GGG.
.#G#G#G#G
…….#..G
G#.###.#G#G
GG.GGG.#.GG
G#.#G#.#.#.
G…G…..
G#.#G###.#G
…G#GGG.GG
G#.#G#G#.#G
GG.GGG#G.GG
#######
(CSDN编辑器的问题,不要在意)
样例输出
10
数据范围限制
30%的数据,保证 N,M<14,并且小星星一定能够抵达最佳炸弹放置点
40%的数据,保证 N,M<14
70%的数据,保证 N,M<101
100%的数据,保证 N,M<2001
100%的数据,保证 X
思路:
其实比赛时就已经想到了,要预处理+搜索
但是比赛时图方便,随手打了个深搜
结果,运行时错误70
后来发现:只能用宽搜打,深搜会炸~!!
代码:
var
n,m,i,j,k,x,y,z,s,ls:longint;
st:ansistring;
a:array[0..2002,0..2002]of char;
f:array[0..2002,0..2002,1..4]of longint;
b:array[0..2002,0..2002]of boolean;
o:array[1..4,1..2]of longint=((-1,0),(0,1),(1,0),(0,-1));
d:array[0..10000001,1..2]of longint;
begin
assign(input,'boom.in');
reset(input);
assign(output,'boom.out');
rewrite(output);
readln(n,m,x,y);
for i:=1 to n do
begin
readln(st);
for j:=1 to m do
a[i,j]:=st[j];
end;
for i:=1 to n do
for j:=1 to m do
if (a[i,j]='G')or(a[i,j]='.') then
begin
if a[i-1,j]='G' then f[i,j,1]:=f[i-1,j,1]+1
else f[i,j,1]:=f[i-1,j,1];
end;
for i:=n downto 1 do
for j:=1 to m do
if (a[i,j]='G')or(a[i,j]='.') then
begin
if a[i+1,j]='G' then f[i,j,2]:=f[i+1,j,2]+1
else f[i,j,2]:=f[i+1,j,2];
end;
for i:=1 to n do
for j:=1 to m do
if (a[i,j]='G')or(a[i,j]='.') then
begin
if a[i,j-1]='G' then f[i,j,3]:=f[i,j-1,3]+1
else f[i,j,3]:=f[i,j-1,3];
end;
for i:=1 to n do
for j:=m downto 1 do
if (a[i,j]='G')or(a[i,j]='.') then
begin
if a[i,j+1]='G' then f[i,j,4]:=f[i,j+1,4]+1
else f[i,j,4]:=f[i,j+1,4];
end;
i:=0;
j:=1;
d[1,1]:=x;
d[1,2]:=y;
b[x,y]:=true;
while ido
begin
inc(i);
x:=d[i,1];
y:=d[i,2];
if f[x,y,1]+f[x,y,2]+f[x,y,3]+f[x,y,4]>s then
begin
s:=f[x,y,1]+f[x,y,2]+f[x,y,3]+f[x,y,4];
end;
for k:=1 to 4 do
if (x+o[k,1]>0)and(x+o[k,1]<=n)and(y+o[k,2]>0)and(y+o[k,2]<=m)and(a[x+o[k,1],y+o[k,2]]='.')and(b[x+o[k,1],y+o[k,2]]=false) then
begin
inc(j);
d[j,1]:=x+o[k,1];
d[j,2]:=y+o[k,2];
b[x+o[k,1],y+o[k,2]]:=true;
end;
end;
writeln(s);
end.