什么是特征向量和特征值

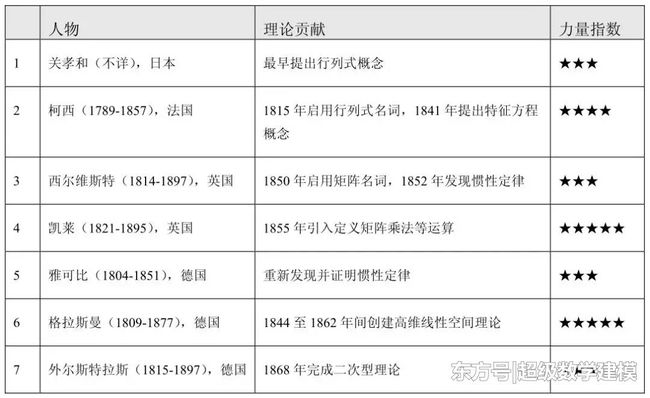
有振动

就有特征值

1

特征值和特征向量的由来

谈到线性代数课本里面的一些概念，比如行列式、矩阵乘积、线性变换、二次型等，或许很少人知道它们是谁发现的，这不像高数/数分课本上那么明显：柯西收敛准则、拉格朗日中值定理、魏尔斯特拉斯判别法。

下面用一个表格来总结一下线性代数的发展史上做出重要贡献的数学家：

其实，在北宋时期，我国就与发现矩阵特征值理论的机会擦肩而过。

在古代，洞房是一件很美好的事，正所谓“春宵一刻值千金”，但是有一位诗人洞房就没有那么简单了。他就是秦少游（1049年—1100年9月17日），在洞房之前却需要回答娘子出的三道难题，其中最后一道是给出上联：闭门推出床前月，要求作出下联。秦少游一时没有头绪，当他看到苏东波往池塘里扔了一颗小石头后，得到一句“投石冲开水底天”的泡妞下联后，就猴急猴急地去洞房了，完全没有想到层层水波中隐含着矩阵的特征值及特征向量的科学大道理。

秦少游

大概地说，水面附近的任一点水珠在原处上下振动（实际上在做近似圆周运动），并没有随着波浪向外圈移动，同时这些上下振动的水珠的幅度在渐渐变小，直至趋于平静。在由某块有着特定质量和形状的石头被以某种角度和速度投入某个面积和深度特定的水池中所决定的某个矩阵中，纹波荡漾中水珠的渐变过程中其特征值起着决定性的作用，它决定着水珠振动的频率和幅度减弱的衰退率。

所以这功劳就给了英国的数学家凯莱(A.Cayley，1821-1895)，他首先把矩阵作为一个独立的数学概念提出来，并在1858年发表了论文《矩阵论的研究报告》，系统地阐述了关于矩阵的理论。文中他定义了矩阵的相等、矩阵的运算法则、矩阵的转置以及矩阵的逆等一系列基本概念，指出了矩阵加法的可交换性与可结合性。

另外，凯莱还给出了方阵的特征方程和特征值以及有关矩阵的一些基本结果。

矩阵论的创立者

好了，现在超模君就说一下它们的定义吧：

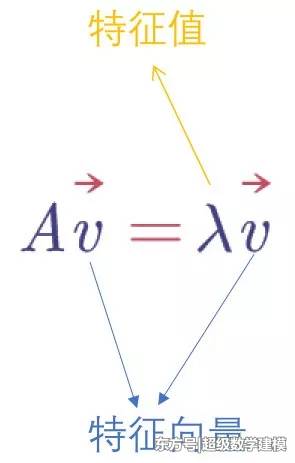
对于给定矩阵A，寻找一个常数λ（可以为复数）和非零向量x，使得向量x被矩阵A作用后所得的向量Ax与原向量x平行，并且满足Ax=λx。

2

特征值和特征向量的几何意义

看到硬生生的定义，模友估计会感到有点迷糊，那超模君就再从几何角度来讲一下它们到底是什么东西：

我们以一个恋爱故事为栗子：

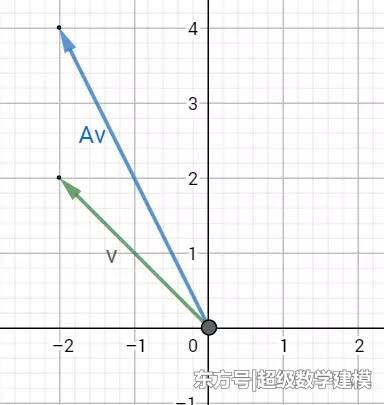
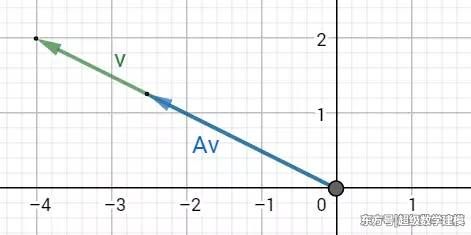
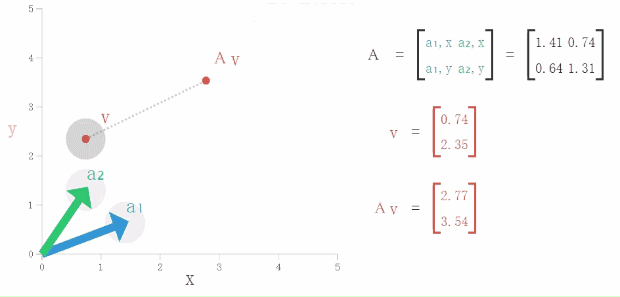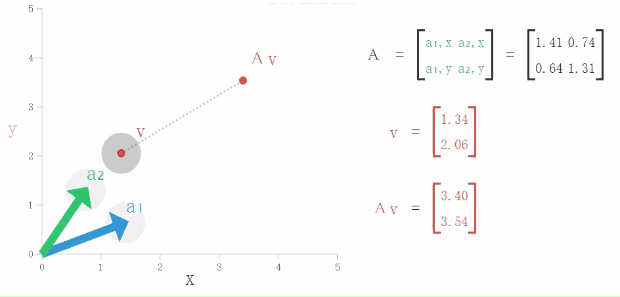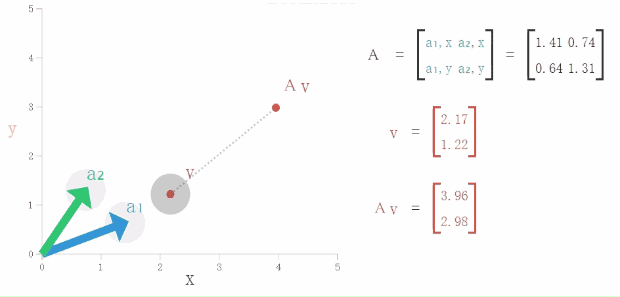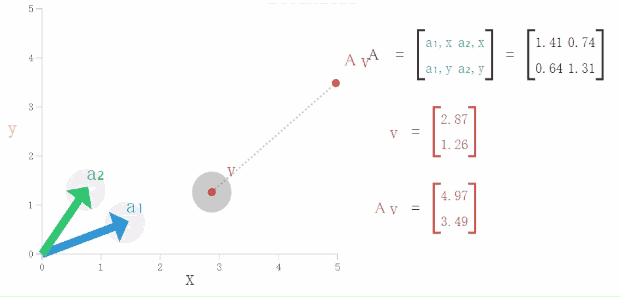
二维公园（坐标轴）里的椅子上有一个孤独的向量v（-2，2），一个忠心（不变）的矩阵A试图从左边搭讪向量v，于是他们坐在一起得到向量Av

他们就开始上谈天文，下聊地理。秀外慧中的向量v彻底迷住了矩阵A，待到离别时，A心里始终放不下v，当v去一个地方的时候，Av（A心里有着v，不是单纯的A）也陪着她去，就这样经历漫长的约会和成长（即下图中的向量v从左边移到右边），终于……

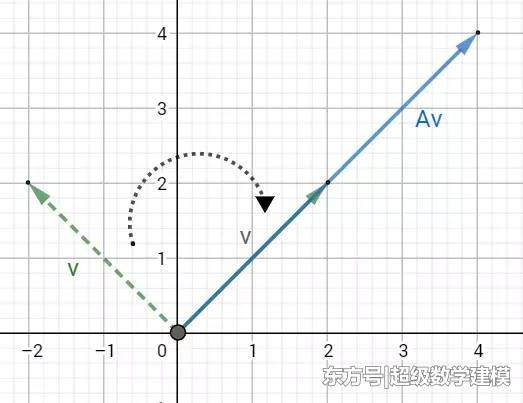
向量v和Av结婚了（共线）！结婚后的向量v多了一份名义，叫做特征向量。而且向量Av的责任也变多了（上图是向量Av相对向量v来说伸长了）。也就是说，向量v与矩阵A的结婚后，向量Av保持忠心（方向）不变，责任变多了或什么东西变少了（进行比例为λ的伸缩）。

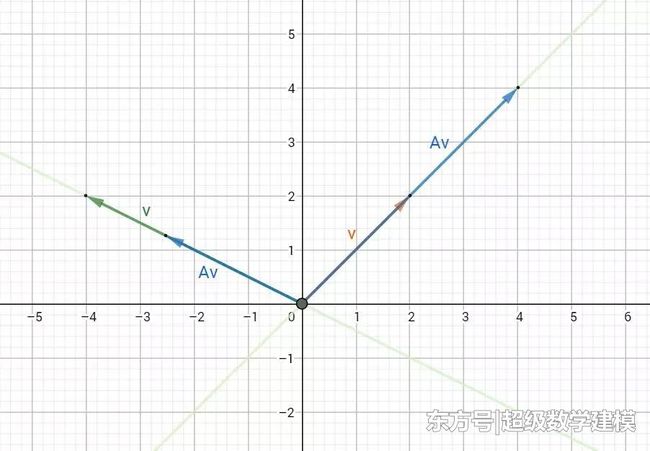
那么我们也许会问：什么东西会变少呢？在恋爱中，向量v喜欢去爬山，向量Av喜欢玩游戏，他们一起度过许多美好时光。

结婚后，向量Av的责任变多了，要撑起这一个家，把更多心思花在孩子教育上，兴趣爱好变少了（上图中容易看出这时候向量Av相对向量v来说“缩短”了）。责任对应的特征值大于1（伸长），兴趣爱好对应的特征值小于1（缩短）。

随着时间的流逝（上下移动v）我们还发现，有两条直线上有着v和Av的所有踪迹，这就是他们的生活空间（特征空间）。换句话说，特征空间包含所有的特征向量。

下面的一个类比可以帮助我们更好的理解特征值和特征向量：

如果把矩阵看作是运动，那么特征值就是运动的速度，特征向量就是运动的方向。

特征向量在一个矩阵的作用下作伸缩运动，伸缩的幅度由特征值确定。特征值大于1，所有属于此特征值的特征向量变长；特征值大于0小于1，特征向量缩短；特征值小于0，特征向量缩过了界，反方向到原点那边去了。

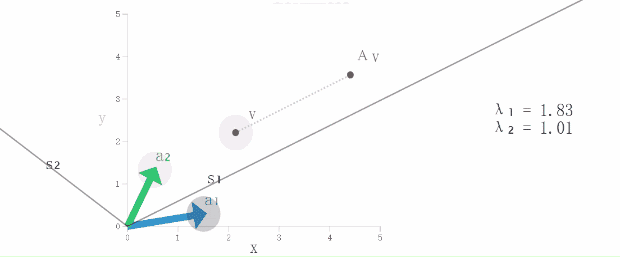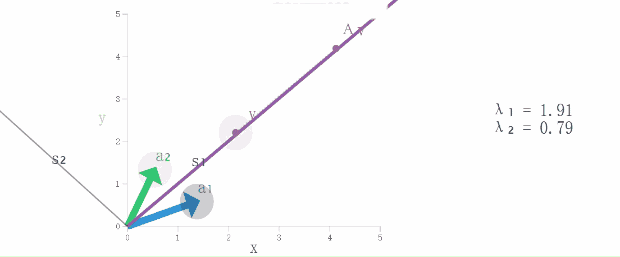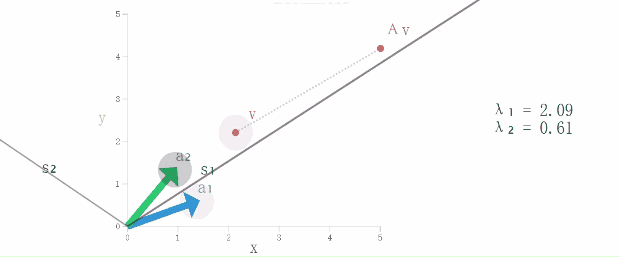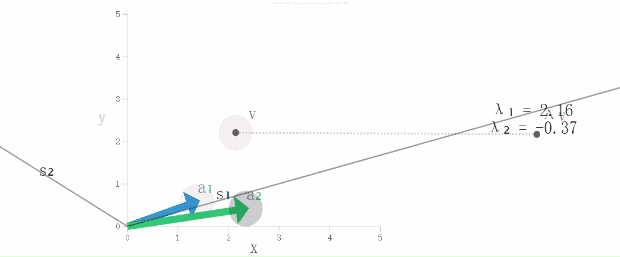
为了让模友们看清楚它们的变化，超模君做了几个动图，我们来感受一下吧：

（1）首先，我们通过改变向量v的位置，看看向量Av有什么变化（矩阵A不动噢）

（2）然后，我们不要动向量v，改变矩阵A每一列（通过移动a1和a2），再看看向量Av有什么变化

（3）接下来是见证奇迹的时刻！看看超模君的金手指怎么移动向量v使它变成特征向量吧！（不好意思，在上移的时候手抖了一下）

（4）最后，我们改变矩阵A（通过移动a1和a2），重点看看特征空间（S1和S2）是怎么变化（特征值也会发生变化哟）

3

特征值和特征向量的应用

说了这么多，可能有模友会问：到底特征值和特征向量有什么用呢？不会仅仅用来考试吧！

其实，特征值和特征向量在我们的生活中都是非常普遍的。

(1)可以用在研究物理、化学领域的微分方程、连续的或离散的动力系统中。例如，在力学中，惯量的特征向量定义了刚体的主轴。惯量是决定刚体围绕质心转动的关键数据；

(2)数学生态学家用来预测原始森林遭到何种程度的砍伐，会造成猫头鹰的种群灭亡；

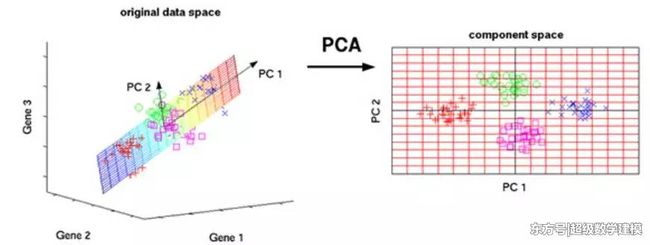
(3)著名的图像处理中的PCA方法，选取特征值最高的k个特征向量来表示一个矩阵，从而达到降维分析+特征显示的方法，还有图像压缩的K-L变换。再比如很多人脸识别，数据流模式挖掘分析等方面。

(4)在谱系图论中，一个图的特征值定义为图的邻接矩阵A的特征值，或者（更多的是）图的拉普拉斯算子矩阵，Google的PageRank算法就是一个例子。

有一句话说得好：“只要有振动就有特征值，即振动的自然频率”。如果你曾经弹过吉他，你已经求解了一个特征值问题。。。

转自：http://mini.eastday.com/bdmip/180328092726628.html