最短路径(Dijkstra)
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止
基本思想
-
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
-
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
-
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是”起点s到该顶点的路径”。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 … 重复该操作,直到遍历完所有顶点。
操作步骤
-
初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
-
从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
-
更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
-
重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
图解
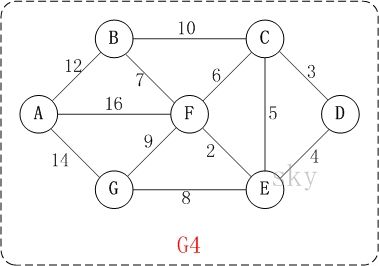
以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。以下B节点中23应为13。
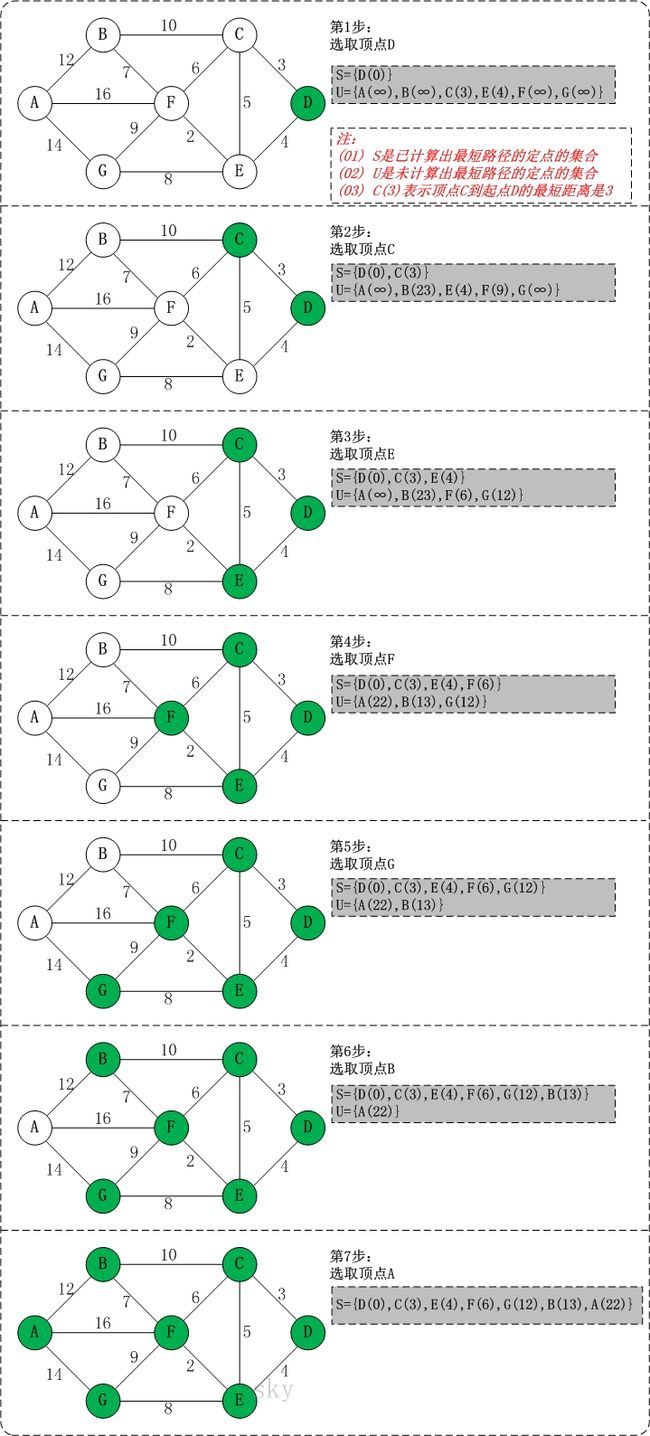
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
例题
Problem Description
给定一个带权无向图,求节点1到节点n的最短路径。
Input
输入包含多组数据,格式如下。
第一行包括两个整数n m,代表节点个数和边的个数。(n<=100)
剩下m行每行3个正整数a b c,代表节点a和节点b之间有一条边,权值为c。
Output
每组输出占一行,仅输出从1到n的最短路径权值。(保证最短路径存在)
Sample Input
3 2 1 2 1 1 3 1 1 0
Sample Output
1 0
#include
using namespace std;
int map1[110][110];
int visit[110];
int dis[110];//记录顶点到其他点的距离
const int INF=0x3f3f3f3f;
int n,m;
void Dijkstra(int t){
visit[t]=1;
for(int i=1;i<=n;i++){//dis数组的初始化
dis[i]=map1[t][i];
}
for(int i=0;idis[x]+map1[x][i]){
dis[i]=dis[x]+map1[x][i];
}
}
}
}
int main()
{
while(cin>>n>>m){
memset(visit,0,sizeof(visit));
int a,b,c;
//初始化map1
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(j==i) map1[i][j]=0;
else map1[i][j]=INF;
}
}
//输入值
while(m--){
cin>>a>>b>>c;
if(map1[a][b]>c){
map1[a][b]=map1[b][a]=c;
}
}
if(m==0) cout<<"0"<