常用时序预测模型的R实现 二
准备知识
这个系列偏重实践。要学飞行,第一步是了解飞行前做什么准备以及什么状态的飞机可以放心上去飞,想造飞机了再去了解发动机怎么工作气动外形有何影响。类似的,实现预测模型,第一步则是了解常用的数据预处理方法以求能让模型跑起来,学会判断模型好坏以保证预测结果是靠谱可用的。具体怎样优化模型不在这个系列里详谈。
数据预处理
在Python的世界里,Pandas就自带很方便的时间戳转换, resample, slicing之类,基本是标准化的数据处理库。在R里有所不同,常用的时间序列类有ts, zoo, xts,还有一大堆不同的时间格式。xts是zoo的subclass所以能做zoo的一切,两者基本结构都是带时间戳的矩阵,而且基本能接受任何格式的时间戳。ts仅接受时间轴上均匀分布的点,而且需要指定起点时间和周期长度,而zoo和xts能接受不均匀的分布。xts在这个系列里仅用于把不那么好预处理的数据转为ts格式,不作详细讨论。以下是ts最关键的初始化代码:
ts(1:10, frequency = 7, start = c(12, 2))
这行意思是什么呢?1:10是数据序列,frequency是指定这个数据序列的周期是7(每个周期里有7个值),start里接受的两个参数,第一个数12是说这个序列的初始周期序号为12,第二个数2是说这个序列的第一个值是周期中的第2个值。打印出来是什么情况呢?
> print( ts(1:10, frequency = 7, start = c(12, 2)), calendar = TRUE)
p1 p2 p3 p4 p5 p6 p7
12 1 2 3 4 5 6
13 7 8 9 10这里用了calendar模式以突出序列的第一个值是周期中的第二位。再看个更贴近生活的例子:
x <- ts(Weekly,start=c(2010,48),frequency=52)Weekly这个序列里存着销售数据,是从2010年的第四十八周开始记录的,记录频率是每周一次,也即这一列中的每一行都是一周的销售量。为何要用ts这个类?因为autoplot, forecast等类都以它作为输入格式。比如可以用刚才的x得到时序图:
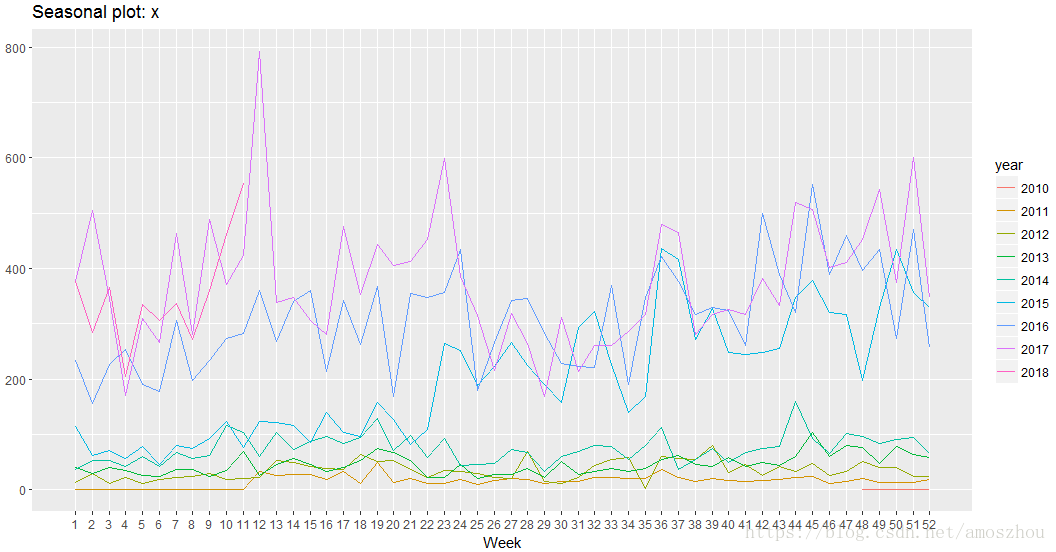
autoplot(x)注意观察时序图中曲线是不是从2010年的最后一个月开始的?销量的确直到2011年才开始为正值,但序列却已经开始了。类似的无脑方法还有很多,比如按不同周期标注不同颜色从而可以在同一个周期长度上比较不同周期观测值的:
ggseasonplot(x) #这里放个彩蛋,这个函数可以加一个参数 polar = TRUE,看看变多帅了?对于周期长的序列尤其好用还有观察周期中每个时位数值变化范围的
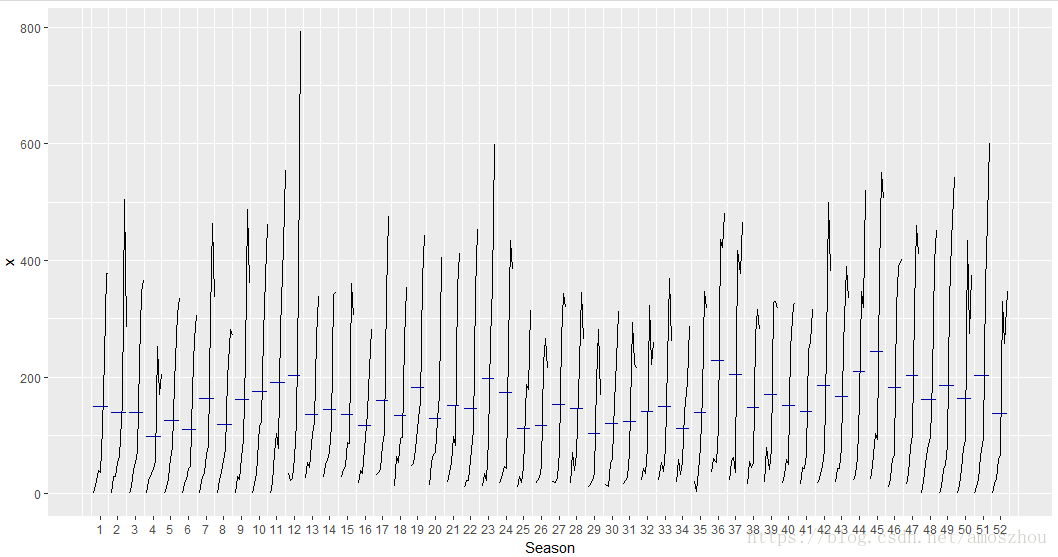
ggsubseriesplot(x)如果需要slice到特定时间域怎么办呢?有个window函数很好使:
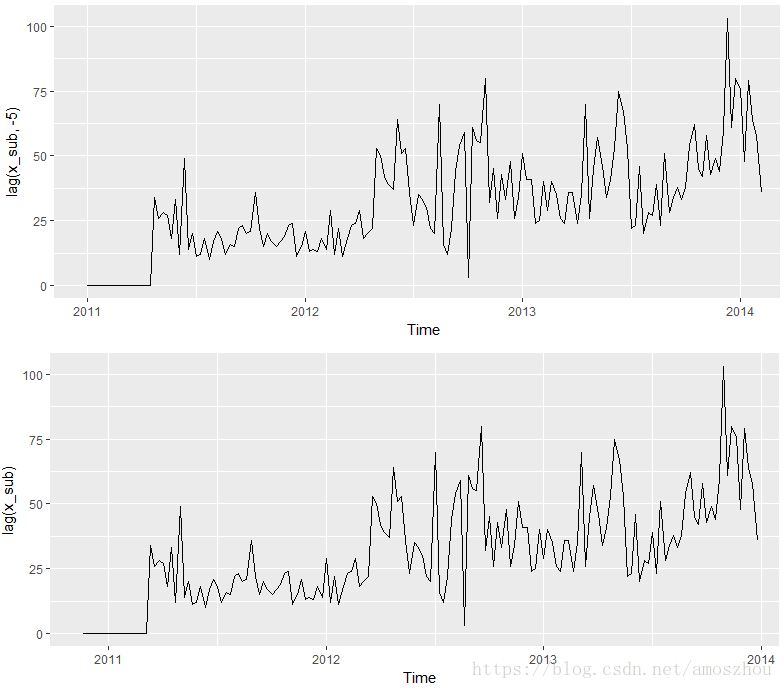
> x_sub = window(x, start=2017)
> autoplot(x_sub)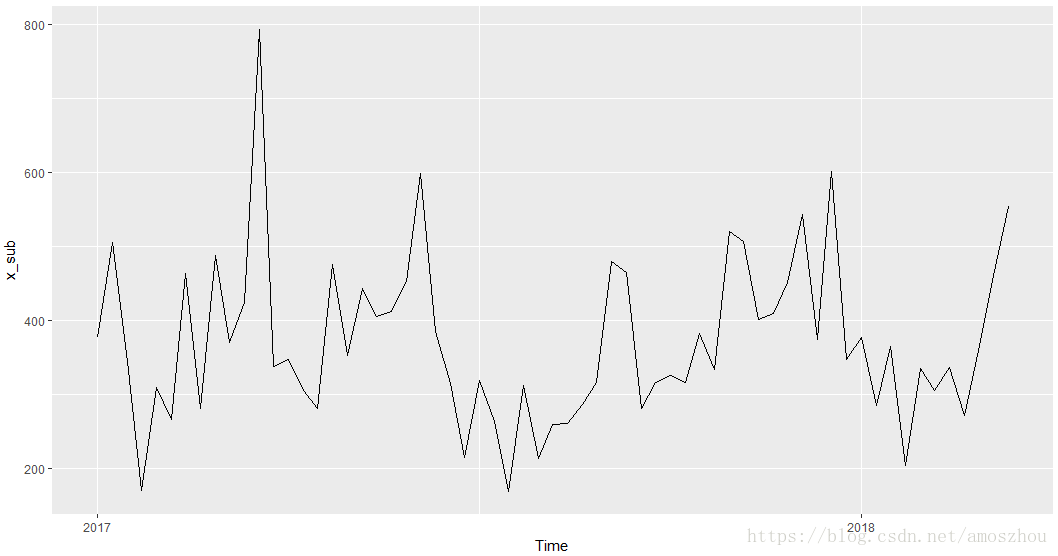
怎样判断到底是否存在季节性
时序数据有季节性的很多,像电力消耗,降雨量,气温。有时候甚至存在周期套周期的情况,术语叫multiseasonal。比如零售业销售数据,不同季节因为气温、节假日体现出周而复始年年相似的模式,但这个大的周期里,每个礼拜又因为工作日和周末的关系存在周期性,而小到每一天,又由于作息导致存在24小时的周期律。
有些时序数据中周期性却不那么显著。比如股票。比如Apple,每年发布新款的时间是固定的,那段时间大概要涨一涨,但谁也不知道下一个新款是不是依然那么受欢迎?又或者不巧碰倒金融危机?很多外部噪声可以破坏掉内生的规律。好在有一种专用的图表就是用来检视周期性的,叫ACF,Auto Correlation Function。它的原理是拿当下的时间序列和lag N的序列做比较,看相关系数为多少,N=1的时候就是和往前移一个时位形成的序列比,N=2和往前移两位比,如此递推。
lagged<-lag(x_sub,-5)lag函数可以用于取得lag后的序列,注意第二个参数是往前推的相位,如果为负值就成了往后推了
有了ACF函数,就不需要自己一个个相位去做比较,它全部一锤子买卖搞定:
> ggAcf(x_sub)大于0.5就是比较强的correlation了,算比较显著的周期性。注意不要和Acf函数混淆,Acf是从lag=0开始的,也就是自己和自己比,那correlation当然是1了,会导致整个图的scale变得头重脚轻。
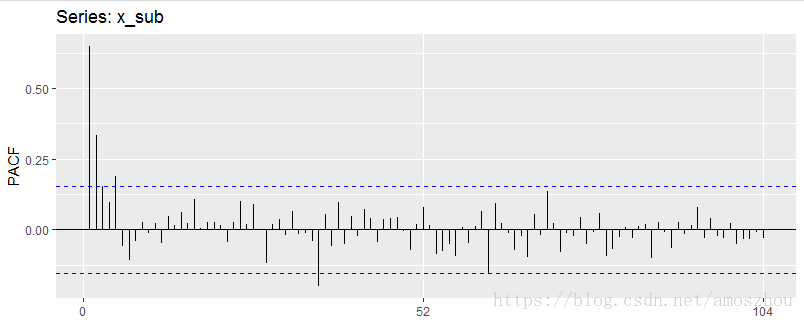
还有值得一提的一个函数是ggPacf,也就是auto correlation function前面加了个partial。这个函数考虑到了不同的lag值可能被共同的变量影响了。比如4周的周期必然导致8周、12周也都显著。排除掉这个因素,绘制pacf会得到如下结果
> ggPacf(x_sub)残值和白噪声
残值即residual,是预测值和实际值之间的差别。在判断一个模型好坏时,一个标准是残值是否为白噪声,也就是说不再含有任何可以被模型学到的信息(趋势,周期性)。怎样的残值是白噪呢?如果它是个均值为零的随机正态分布就基本可以判断是白噪。均值不为零其实关系也不大,只要把预测值shift一下就好了。在Python里这些都要自己写,但在R里又有个强大的函数把这事情干了,
> fit <- auto.arima(x_sub)
> checkresiduals(fit)
Ljung-Box test
data: Residuals from ARIMA(0,1,1)(0,0,1)[52]
Q* = 112.62, df = 102, p-value = 0.222
Model df: 2. Total lags used: 104auto.arima是在建立预测模型,具体怎么干的下一篇再讲。运行结果既包括那个Ljung-Box test又包括如下图表:
图表显示的,正是白噪声。而Ljung-Box test里最重要的一项结果就是p-value=0.222,它代表的也即是残值确实为白噪(p<0.05则说明非白噪了)
以上为准备知识。下一篇开始正式介绍预测模型。
上一篇 常用时序预测模型之背景 下一篇 常用时序预测模型之ETS